Table of Contents
Amplitude Formula: Amplitude is one of the main concepts in physics which deals with the movement of particles. The amplitude formula is used to find the amplitude of a certain object. The amplitude is the value associated with the displacement of the object. Periodic motion is one such motion where this concept is widely used. Period motion is basically a type of motion that repeats its characteristics after a certain period of time. Objects moving in periodic motion, particularly moving in SHM (Simple Harmonic Motion) or an Oscillatory motion, create an amplitude, which is then measured by this formula.
Amplitude Formula
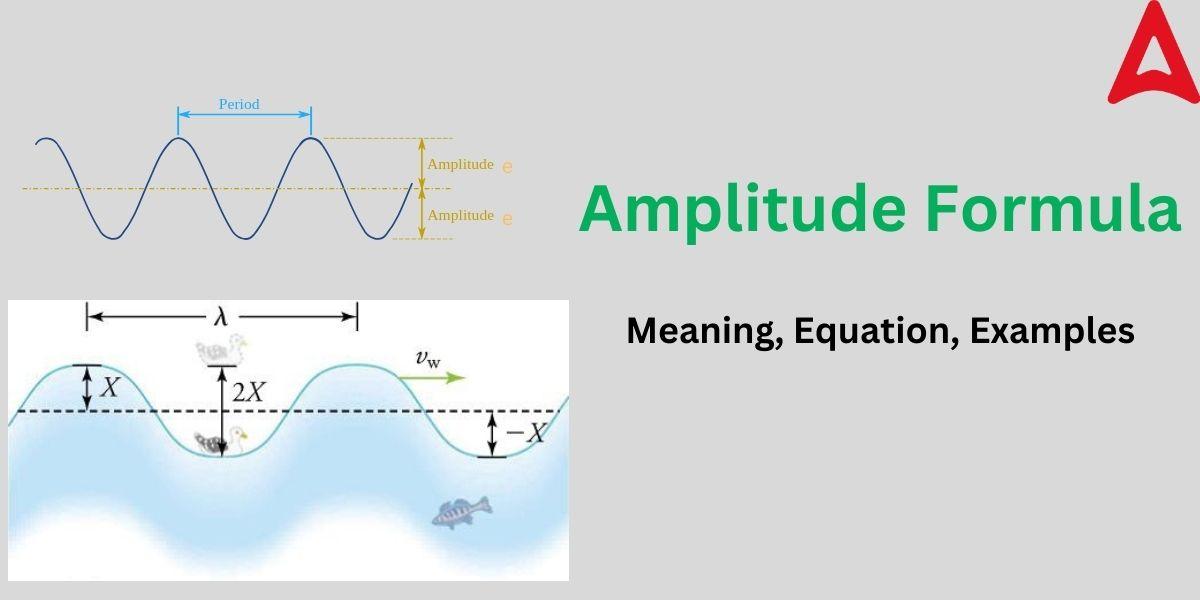
Before understanding the Amplitude formula, let us understand the term amplitude. As mentioned in the name of this formula, it is used to derive the value of the amplitude. Amplitude is the maximum displacement of an object from its mean position or the position of equilibrium. The object moving in a periodic motion follows a wave pattern when plotted on a 2D plane. The maximum displacement of an object from its equilibrium position is commonly used to characterize the amplitude of an oscillatory motion. Depending on the circumstances of the oscillation, the amplitude calculation formula differs. The basic formula for the amplitude is given by:
X = (Ymax – Ymin)/2
where, X = amplitude
Ymax = maximum displacement from the mean position
Ymin = minimum displacement from the mean position.
Amplitude Formula in SHM
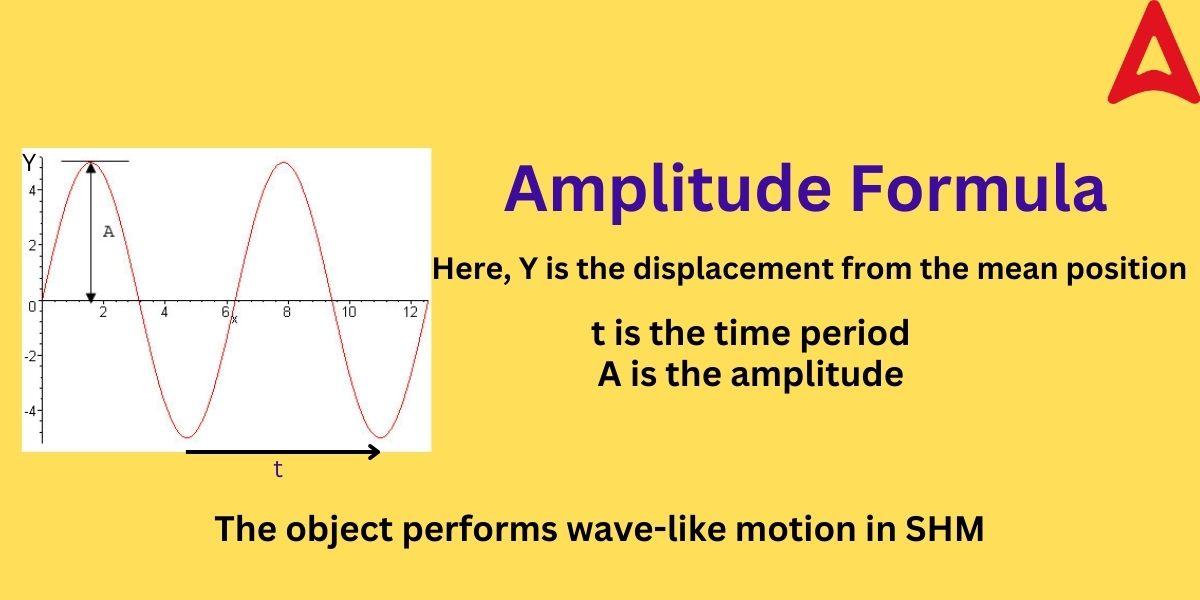
As mentioned earlier, the formula to derive the amplitude depends on the type of oscillatory motion. The formula to derive the value of amplitude in SHM (Simple Harmonic Motion) is known as the amplitude formula in SHM or the amplitude formula in waves. A simple harmonic motion is a repeating back-and-forth movement of an object (a spring) through an equilibrium, or mean position, with the goal of maintaining an equal distance between the maximum displacement on either side of the position. The SHM forms a wave like motion when shown on a cartesian plane.
The formula to find the amplitude in SHM or waves is given by:
Y = A sin (ωt + Φ)
or
Y = A cos (ωt + Φ)
where, A = amplitude
Y = displacement of the object from the mean or equilibrium position
t = time period
ω = angular frequency
Φ = phase angle
It must be noted that the ω (angular frequency) is measured in terms of radian per second. As you can observe from the above equations that the object in SHM forms a wave (a function of sin and cos trigonometric ratios).
Amplitude Formula with Frequency
The above formula can be modified to establish the relation between the amplitude and frequency. As we know, frequency is the occurrence of a particular event in 1 second. In SHM, the number of waves formed in a second is known as its frequency. The formula for the amplitude with Frequency is expressed as:
Y = A sin (2Πft + Φ)
or
Y = A cos (2Πft + Φ)
where, A = amplitude
Y = displacement of the object from the mean or equilibrium position
t = time period
f = frequency
Φ = phase angle
This mathematical equation between amplitude and frequency has been obtained by substituting the value of angular frequency (ω) as 2Πf.
Amplitude Formula Wavelength
We can find the wavelength of a particular wave in SHM by finding out its frequency using the formula for amplitude. The wavelength in SHM is the distance between the mid-points of one crest to another (highest amplitude value in +Y direction) or the distance between the midpoints of one trough to another trough (highest amplitude value in -Y direction). The wavelength is denoted by λ. We can find out the wavelength using the relation given below.
frequency (f) = velocity of the wave (v)/wavelength (λ)
We can use this equation to substitute the value of f in the amplitude formula with frequency. The modified formula for the amplitude will now relate the wavelength to the amplitude of the SHM object.
Y = A sin ((2Πvt)/λ) + Φ)
or
Y = A cos ((2Πvt)/λ) + Φ)
where, v = velocity of the wave
λ = wavelength
Amplitude Formula Dimensions
This formula can be used to find the dimensional value of the amplitude. As we know that amplitude is basically the displacement from the mean position, so, its dimensional formula will be same as that of the displacement. Using the Amplitude formula, we can say that the SI unit of the amplitude is Meter (m). So, the dimensional formula for the amplitude becomes [L¹] which can be verified using the amplitude formula.
Amplitude Formula in Physics
Amplitude is a crucial metric that describes the extent of an object’s departure from its equilibrium position in the context of oscillatory motion. Understanding amplitude is essential whether we are investigating the straightforward harmonic motion of a pendulum, the vibrations of a guitar string, or the oscillations of a spring. So, this formula finds a very special position in the world of physics. It is an important formula that explains the nature of SHM and is one of the most important concepts in Class 11 physics. Through this article, students will get a clear understanding of this topic in a detailed manner.
Amplitude Formula Solved Examples
Some of the solved questions related to this topic is given below. These solved examples will help students in understanding how to apply the amplitude formula in solving a problem.
Example 1: The wave equation of a particle performing SHM is given as X = 9 Cos4t. What will be the frequency of that particle performing SHM?
Solution: As we know, the standard amplitude formula with frequency states Y = A Cos2Πft
On equating the provided equation with the standard equation, we get
2Πf = 4 rad/s
or, f = 4/2Π
f = 2/Π
or, frequency (f) = 7/11 Hertz
Example 2: The wave equation of an object performing SHM is given by 5Y = 20 Sinωt. What will be the value of the amplitude?
Solution: Given equation for the wave is 5Y = 20 Sinωt
Comparing it with the standard amplitude formula Y = A Sinωt
On modifying the given equation in the standard form, we get:
Y = (20 Sinωt)/5
or, Y = 4 Sinωt
On comparing, we get A = 4
Hence, the amplitude = 4 m
Example 3: What will be the angular frequency and amplitude of the wave expressed by the equation X = 20 cos (17t + 1)?
Solution: Given wave equation: X = 20 cos (17t + 1)
By comparing it with the standard amplitude formula Y = A cos(ωt + Φ)
We get amplitude (A) = 20 m
Angular Frequency (ω) = 17 rad/s




 Critical Angle: Definition, Formula, Der...
Critical Angle: Definition, Formula, Der...
 Physics Investigatory Project Class 12: ...
Physics Investigatory Project Class 12: ...
 Ohm's Law Statement, Definition, Derivat...
Ohm's Law Statement, Definition, Derivat...































