Types of Fraction: When a component or number has been split into a number of equal pieces and a few of these parts are taken, the ratio of the taken object to the overall object is expressed as Fraction. There are 4 major types of fractions and in total 7 types of fractions. The fractional bar separates the numerator (upper number) from the denominator (bottom number) in a fraction eg –
. The denominator reflects the total number of items in a group or the number of equal pieces divided into the whole. The numerator is the number of parts of the whole or the number of objects taken from the group. In this post, we will study different types of fractions in depth and their properties.
Types of Fraction Definition
A fraction is a portion of whole objects. In mathematics, a fraction is defined as a number value that represents a portion of a whole or set of things. The first ancient record of fractions was discovered in ancient Egypt when Egyptians employed fractions for portioning rations, kingdom-related purposes, crops, and other food.
Let us use an example to better grasp fractions. A cake is cut into six equal pieces. Each slice of the entire cake represents, which symbolizes 1 of 6 equal pieces. The fraction 1/6 is pronounced ‘1 by 6’. Because all measured amounts in real life cannot be absolute whole numbers, we must rely on fractions to convey the quantity.
Types of Fraction with Examples
Every type of fraction is made up of two numbers: one at the top and one at the bottom, separated by a horizontal bar. There are 7 types of fractions based on the numerator and denominator. The following section of the article discusses the different types of fractions with examples and an illustration. The seven types of fractions are mentioned below.
- Unit Fraction
- Proper fraction
- Improper fraction
- Mixed fraction
- Like fractions
- Unlike fractions
- Equivalent fractions
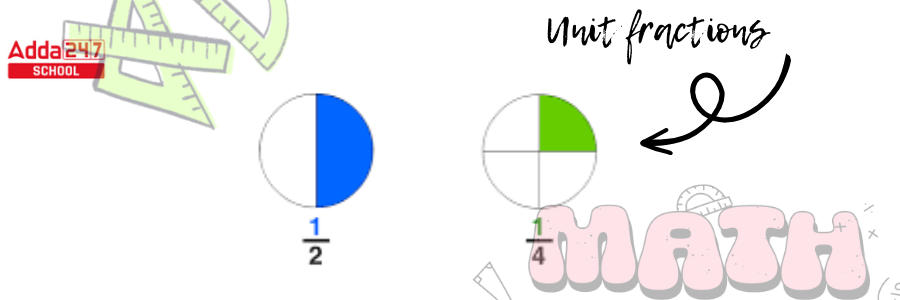
Unit Fraction
- Unit fractions have a numerator of 1 and a denominator of any natural number.
- Unit fractions are all fractions with 1 as the numerator. We choose only one portion of the whole, which is divided equally into a finite number of parts, in these fractions.
- It has the formula 1/x, where x∈N. Some instances of unit fractions are 1/6, 1/7, 1/124, and so on.
Proper fraction
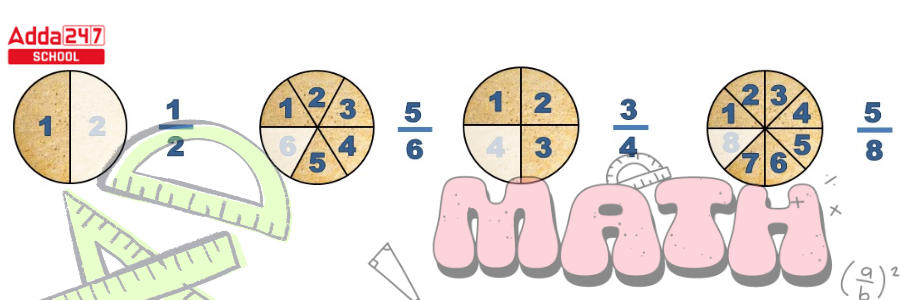
- The numerator (number of equal parts counted/upper part) of a proper fraction is a smaller number than the denominator (total number of parts/lower portion).
- All of these fractions are smaller than one on the number line.
- A proper fraction is less than 1 as the numerator is less than the denominator.

- Proper Fraction explanation with example – We can see in the pictures that one cake has been cut into a variety of pieces. The top number / numerator indicates the number of pieces. The bottom number / denominator indicates how many equal pieces are sliced into the cake.
In the first picture, you get one piece of cake, whereas in the second picture, you get five pieces out of six. As you can see, the total number of cake pieces (denominator) is greater than the number of pieces you get to eat (Numerator).
Improper fraction
- If the numerator (number of equal parts tallied/ upper part of a fraction) exceeds the denominator (total number of parts), an improper fraction is formed.
- These fractions are bigger than one.
- Improper fractions extend beyond one on the number line.
- Proper fractions are used when more than one thing has been split into equal halves. The denominator represents the number of equal components. The number of available components is represented by the numerator.
- Example – All of the numerators in this image are greater than the denominator.
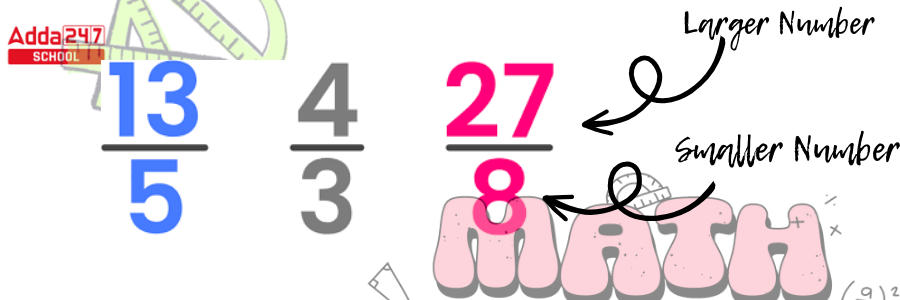
Mixed fraction
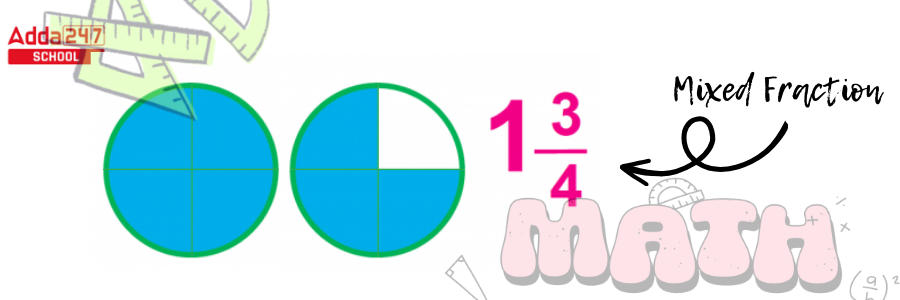
- Mixed fractions are made up of both a whole integer and a proper fraction.
- Because mixed fractions are made up of whole numbers and fractions, they are always bigger than one.
A mixed number is composed of a whole number and a fraction, as shown in this figure, where 1 is a whole number and 3/4 is a suitable fraction. - Mixed fractions are made up of both a whole integer and a proper fraction.
Because mixed fractions are made up of whole numbers and fractions, they are always bigger than one.
A mixed number is composed of a whole number and a fraction, as shown in this figure, where 1 is a whole number and 3/4 is a suitable fraction. - Example – These two circles have been divided into four parts. The amount of the shape we have can be expressed as a mixed number (
) or as an improper fraction (7/4).
These two circles have been divided into 4 + 4 parts. The amount of the shape we have can be expressed as a mixed number (
) or as an improper fraction (7/4).
Like fractions
- Like fractions are fractions that have the same denominator and different numerator.
- 1/4, 2/4, 5/4, and 7/4 are all Like fractions. The denominator in all of the preceding fractions is the same. That is 4.
- Since all of the denominators are the same, simplifying such fractions is simple. Assume we need to add all of the following similar fractions;
1/4 + 3/4 + 5/4 + 7/4
= (1+3+5+7)/4
= 16/4
= 4
It is evident from the preceding example that adding or subtracting two or more like fractions is simple.
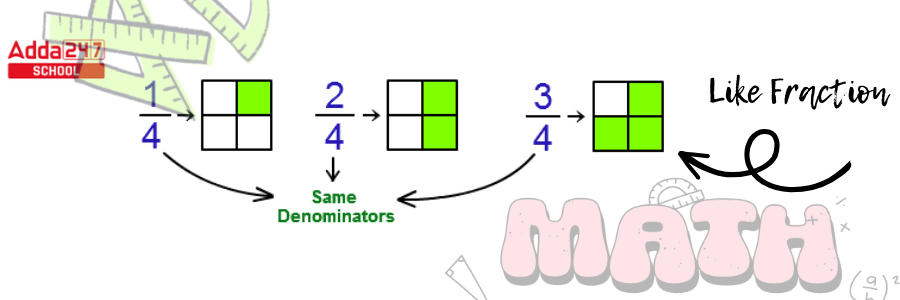
Unlike fractions
- Unlike fractions have different denominators. The denominators of fractions have various values in this case. As a result, unlike fractions are defined as fractions with the same numerator but different denominators.
- 3/6, 6/8, 2/10, 6/2 are some examples. The denominators in the preceding fractions differ. They are numbered 6, 8, 10, and 2. The ‘Unlike Fraction’ instances are clearly depicted in the image below.
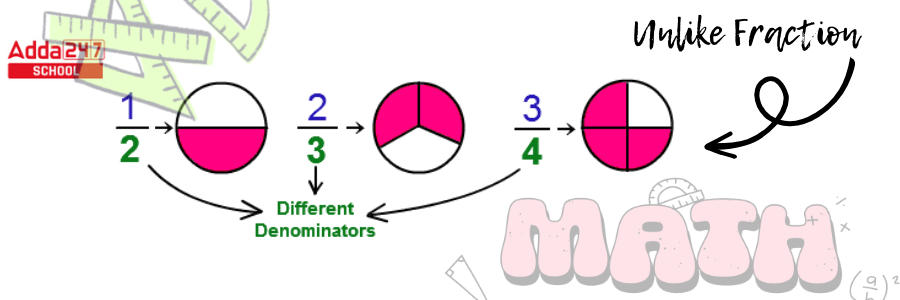
- We must use different procedures when adding or subtracting two or more, unlike fractions.
They do,
1. The method of cross-multiplication
2. The LCM Method
Cross Multiplication Method Example:
Consider the following addition of two fractions.
2/5 + 3/8
The denominators in the preceding two fractions are 5 and 8.
There is no other common divisor for 5 and 8 except 1.
As a result, 5 and 8 are co-prime.
As seen below, we must use the cross-multiplication approach to add the two fractions 2/5 and 3/8.
= [(2 ⋅ 8) + (3 ⋅ 5)]/(5 ⋅ 8)
= [16 + 15]/(40)
=
Equivalent fractions
- Equivalent fractions are those that are equal to one another when, following simplification, two or more fractions provide the same result and constitute the same portion of the total.
- To obtain the equivalent fractions, multiply or divide the provided fraction’s numerator and denominator by the same number.
- Example – 1/2 and 4/8 are Equivalent fractions.
The numbers 2/7 and 6/21 are Equivalent fractions.
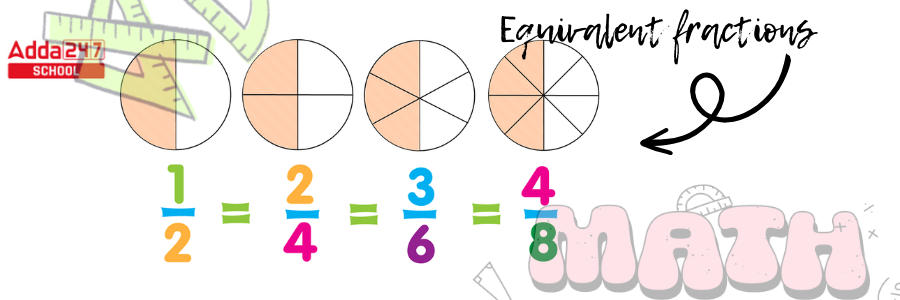
Types of Fraction Worksheet for Class 5 & Class 6
Question 1: What is the simplest form of 12/48?
Answer: The greatest common factor between 12 and 48 is 12.
When we divide the numerator and denominator by 12,
we obtain =
Because 1 and 4 do not have a common factor, 1/4 is the simplest form.








 MGSU Result 2025 Out, Download Maharaja ...
MGSU Result 2025 Out, Download Maharaja ...
 EMS Results 2025 OUT at gnanasangama.kar...
EMS Results 2025 OUT at gnanasangama.kar...
 How to Calculate CUET Score, Check Marks...
How to Calculate CUET Score, Check Marks...









