Rydberg Equation: The Rydberg Equation is a mathematical formula for calculating light’s wavelength. Every element has its own spectral identity. The Rydberg equation can be applied to the spectra of several elements. The wavelength of light generated by an electron traveling between atomic energy levels is predicted by the Rydberg formula. The energy of an electron changes when it moves from one atomic orbit to another. When an electron transitions from a high-energy orbit to a lower-energy orbit, then a photon of light is produced. In this post, we will study the Rydberg equation, the Rydberg formula, its derivation, Rydberg contact, related wavelength, the Balmer Series, and more.
Rydberg Equation
The Rydberg equation or formula is used to calculate the wavelength of light radiated by an electron transportation between an atom’s energy levels. This discovery heralded the start of spectroscopic research. In addition, as an electron transitions from a low-energy state to a higher-energy state, a photon of light gets taken up by the atom. The energy of an electron fluctuates as it moves from one atomic orbital to the next. A photon of light is produced when an electron moves from a high-energy orbital to a lower-energy orbital. When an electron transitions from a low-energy to a higher-energy state, an atom absorbs a photon of light. The Rydberg Formula can be implemented to calculate the spectra of various elements.
Rydberg Equation Formula
The Rydberg Formula has application to the spectra of several elements. The Rydberg Formula is represented as –
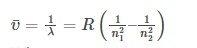
Where
n1 and n2 are integers (n1 < n2),
λ= Photon wavelength,
R = Rydberg constant [1.0973731568539(55) 107 m-1].
R is a constant known as the Rydberg constant, and the formula is generally written as
![]()
The Rydberg Constant is the most precise physical constant. The modern value of the Rydberg constant is 109677. 57 cm-1.
In most circumstances, we’ll be dealing with hydrogen, which permits us to use the formula:
= 1/λ = RH(1/n12 – 1/n22)
Where,
n1 and n2 are integers (n1 < n2),
λ = Wavelength of the photon,
RH = Rydberg constant due to hydrogen [1.0973731568539(55) × 107 m-1].
= 1/λ = 1.0974 × 107(1/n12 – 1/n22)
Derivation of Rydberg Equation
When an electron transitions from one orbit to the next.
ΔE = Ef – Ei
Where,
ΔE is the energy difference,
Ef is the final energy, and
Ei is the initial energy.
According to Bohr’s Model, ΔE = (-RH/nf2) – (-RH/ni2).
ΔE = RH/ni2 – RH/nf2
ΔE = RH(1/ni2 – 1/nf2)
ΔE = RH(1/ni2 – 1/nf2)
∴ ΔE = 2.18 × 10-18(1/ni2 – 1/nf2) ……(First Equation)
E = hv
When we plug the value of E into Equation 1, we get
hv = 2.18 10-18(1/ni2 – 1/nf2).
v = 2.18 × 10-18/h × (1/ni2 – 1/nf2) ⇢ (In which h = 6.626 10-34)
v = 3.29 × 1015(1/ni2 – 1/nf2) ⇢ (Equation 1)
We have c = λv
1/λ = v/c
Divide equation 2 by c to get –
v/c = 3.29 × 1015/c × (1/ni2 – 1/nf2)
= 1/λ = 1.0974 × 107(1/ni2 – 1/nf2) m-1
Rydberg Equation Units
The Rydberg constant R has units of
(Rydberg Equation Unit).
According to the Bohrs formula (where the symbols have their usual meaning) –
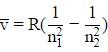
The Rydberg constant R has units of
.
Rydberg Constant
The Rydberg constant in physics is a physical constant related to atomic spectra in the field of spectroscopy. R∞ stands for heavy atoms and RH stands for hydrogen. The Rydberg constant first appeared as a fitting parameter in the Rydberg formula. Neils Bohr later estimated it using fundamental constants.
Equation of Rydberg Constant
Neils Bohr demonstrated the Rydberg Constant equation utilizing basic constants and illustrating relationships utilizing the Bohr model. The Rydberg constant is used in formulas for line wavenumbers in atomic spectra. It is determined by the electron’s rest weight and charge, the speed of light, and Planck’s constant.
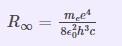
Where me denotes an electron’s rest mass.
The Planck Constant is denoted by h.
c is the velocity of light in a vacuum.
εo is the permittivity of free space.
e is the elementary charge.
Constant Value of Rydberg
The most accurately determined physical constants are R∞ and the electron spin g-factor.
Rydberg Constant Value, R∞ 10973731.568508(65) m-1
Rydberg Constant Value, R∞ 1.097 x 107m-1
- RH 1.09677576 x 107 m1 is the value of the Rydberg Constant for Hydrogen.
Rydberg Equation Wavelength
Several studies have been conducted to explain various aspects of light, such as how it moves, how it reflects, and so on. The spectral series is another essential topic of them. The spectral series is shown by lines.
- The Rydberg formula can be used to compute when an element’s atoms are energized and emit light rays from greater amounts of energy to lower energy levels.
- Understanding the principle of spectral series is made easy by studying the hydrogen atom. We need to put a laser beam into the slit to view these series of the spectrum. When the photos are subjected to a spectroscope, each component of this light beam may generate a separate image, which can seem like some spectral series. The spectral lines or series observed by the spectroscope in a hydrogen atom are known as the Hydrogen Spectrum Series.
- The wavelength of light can affect the gaps (between lines) if the wavelength of the spectral lines is greater the spacing is greater, and the lines appear to be separated from each other. When the wavelength is reduced, the lines become closer and appear to be beside one other.
- The distance between the lines is also noted if the shortest wavelength is observed. This is known as the series limit. We can tell if the volume is high or low by examining this series limit.
- At various levels of the hydrogen atom spectrum, the Spectrum series can be seen in a variety of ways. In the hydrogen Spectrum series, we have numerous classes. One of them uses the Rydberg formula.
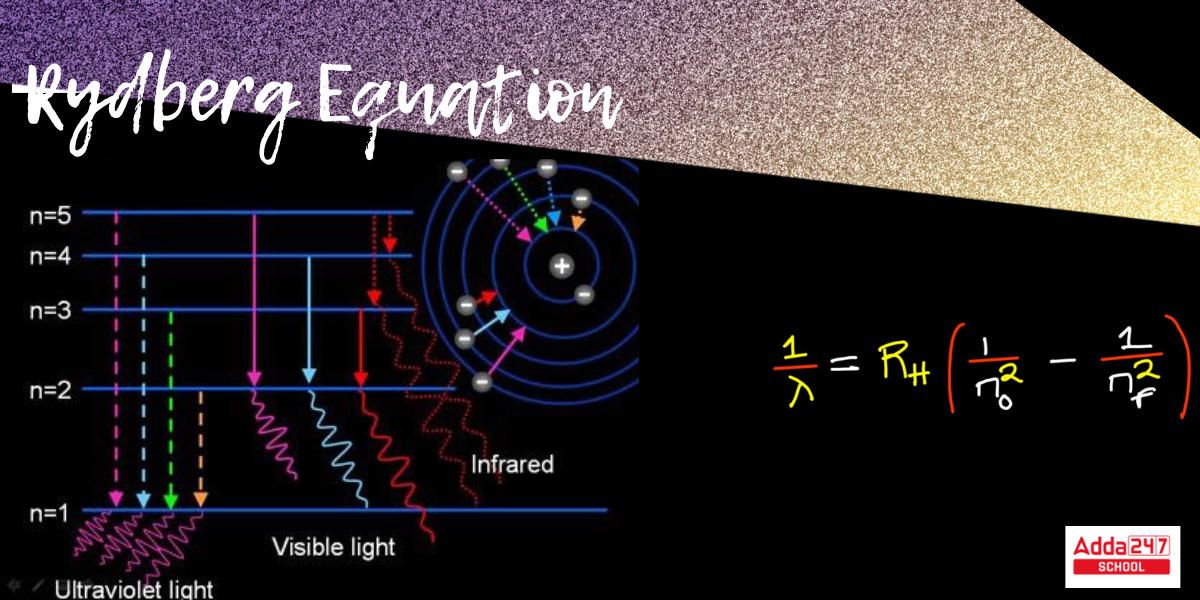
The energized atoms change energy levels because, as we know, the hydrogen spectrum is an emission spectrum. These transitions can be studied by Niels Bohr. To compute the wavelength of these spectral lines, he provided another method known as the Rydberg formula.
![]()
Where Z denotes the atomic number
The lower energy level is denoted by NL.
NH is the higher energy level
𝜆 is the wavelength
R is the Rydberg constant and has the value 1.09737✕107 m⁻¹
Rydberg Equation for Balmer series
- In an astounding display of mathematical instinct, Balmer devised a simple formula to estimate the wavelength of any of the lines found in atomic hydrogen in what is now known as the Balmer series in 1885. Three years later, Rydberg generalized this so that the wavelengths of any of the lines in the spectrum of hydrogen emitted could be determined.
- Rydberg proposed (unaware of Balmer’s work) that all atomic spectra constituted families with this pattern. There are families of spectra that follow Rydberg’s pattern, most notably in the alkali metals, sodium, potassium, and so on, but not with the precision that the hydrogen atom lines fit the Balmer formula, with small values of n2 projected wavelengths that deviated significantly. The Rydberg equation is –
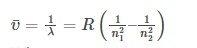
where RH is the Rydberg constant and equals 109,737 cm-1),
and n1 and n2 are integers (whole numbers), with n2 greater than n1.
- n1=2 and n2 can be any whole number between 3 and infinity for the Balmer lines. The many number variations that can be put into this formula allow the calculation of the wavelength of any of the lines in the hydrogen emission spectrum; the wavelengths obtained by this formula and those measured in a real spectrum agree quite well.
- The spectral lines are classified into series based on their n1 values. Lines are called progressively using Greek letters within each series, beginning with the most lengthy wavelength/lowest frequency of the series.
For example, the (n1=1/n2=2) line is referred to as “Lyman-alpha” (Ly- ), but the (n1=3/n2=7) line is referred to as “Paschen-delta” (Pa- ). The primary six series are labeled as follows:
-
- Lyman series, n1=1
- Balmer series, n1=2
- Paschen series (or Bohr series) with n1=3
- Brackett series, n1=4
- Pfund series with n1=5
- Humphreys series, n1=6
Rydberg formula vs. Balmer formula
Difference between the Rydberg formula and the Balmer formula –
The Rydberg formula is an equation for predicting the wavelength of light produced by an electron traveling between different energy levels of an atom. The Rydberg formula has the following mathematical equation-
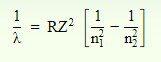
Where is the wavelength of the radiated photon;
R is the Rydberg constant;
Z is the atomic number of the atom under consideration (Z=1 for hydrogen);
n 1 is the lower energy level shell number; and
n 2 is the higher energy level shell number.
The Balmer formula, on the other hand, can only forecast the wavelength of light when an electron passes from the higher shell (higher energy level) to the second energy shell. As a result, for the Balmer series, the value of n 2 is fixed, i.e., n 2=2.
As a consequence, the Balmer formula is –
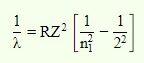








 Try CUET College Predictor 2025 to Predi...
Try CUET College Predictor 2025 to Predi...
 CUET Result 2025 OUT (Today) @cuet.nta.n...
CUET Result 2025 OUT (Today) @cuet.nta.n...
 Why the Delay in CUET UG 2025 Results? C...
Why the Delay in CUET UG 2025 Results? C...









