Parallel Axis Theorem Equations Important points
The following factors need to be taken into account in order to use the parallel axis theorem.
- Axis A and axis B must be parallel.
- The center of mass of the body must be on axis B.
- They must be as close together as is physically practicable.
Must know: What is the Unit of Current, Resistance and Voltage?
Parallel Axis Theorem Examples
Parallel Axis Theorem Q1: If the moment of inertia of a body along a perpendicular axis passing through its centre of gravity is 50 kg·m2 and the mass of the body is 30 Kg. What is the moment of inertia of that body along another axis which is 50 cm away from the current axis and parallel to it? Use Parallel Axis Theorem Formula
Solution: From the parallel axis theorem,
I = IG + Mb2
I = 50 + ( 30 × 0.52 )
I = 57.5 kg – m2
Parallel Axis Theorem Q2: Calculate the moment of inertia of a rod whose mass is 30 kg and length is 30 cm?
Solution: The parallel axis formula for a rod is given as,
I = (1/12) ML2
plugging in the values we get
I = 0.225 Kg m2.
Parallel Axis Theorem Q3: Calculate the moment of inertia of a stick whose mass is 100 gm and length is 10 cm?
Solution: The parallel axis formula for a rod is given as,
I = (1/12) ML2
plugging in the values we get
I = 0.0000833 Kg m2.
Must know: Trigonometry Table- (0 to 360) Formula, Value, Chart, Ratio, PDF for Class 10, 12
Parallel Axis Theorem is useful in finding the Area Moment of Inertia
The parallel axis theorem was developed to determine an object’s moment of inertia when the axis passed outside of the central axis. Because of this, calculations are made to be simple, especially for bodies with irregular shapes. It is possible to use the parallel axis theorem with both 2D and 3D objects.
Even while a 3D item cannot be used as a whole, it can be used if it is broken up into smaller pieces, or laminas. The parallel axis theorem is then used to solve each lamina independently. It only works with stiff bodies. Additionally, there is an inertia matrix that changes depending on the person’s point of reference.
|
Found this article helpful?
Let’s connect via chat or call our senior expert counselor at +91-9625869989 to learn more about the different streams and options available. We would love it if we could add some of your insights. If you have a definite goal of scoring the highest marks, then you can resolve your doubts via our Adda247 app/quizzes and youtube class assistance (https://www.youtube.com/c/Adda247School) |
Parallel Axis Theorem- QNAs
Que. What is the statement of the parallel axis?
Ans. According to the parallel axis theorem, a body’s moment of inertia about an axis that is parallel to its axis of mass is equal to the product of its moment of inertia about its axis of mass, the product of mass, and square of the distance between the two axes.
Que. What are the parallel axis and perpendicular axis theorems?
Ans. The parallel axis theorem states that a body’s moment of inertia about any axis is equal to the product of the body’s mass and the square of the perpendicular distance between the two axes, as well as the moment of inertia about a parallel axis that passes through its center of gravity.
Que. What is the parallel axis theorem used in the moment of inertia?
Ans. According to the parallel axis theorem, a body’s moment of inertia about any axis equals its moment of inertia about a parallel axis through its center of mass plus the sum of its mass and the square of the perpendicular distance between its two parallel axes.
Que. Is the parallel axis theorem always true?
Ans. It is really important to note that the parallel axis theorem is only true for Ic or IG – you cannot use the moment of inertia about another point in this formula. It’s also clear that the added term will always be positive (area, mass, and the squared distance cannot be negative).
Que. What is the formula for parallel axis theorem transfer?
Ans. The parallel axis theorem formula is I=Icm+mr2 I = I c m + m r 2

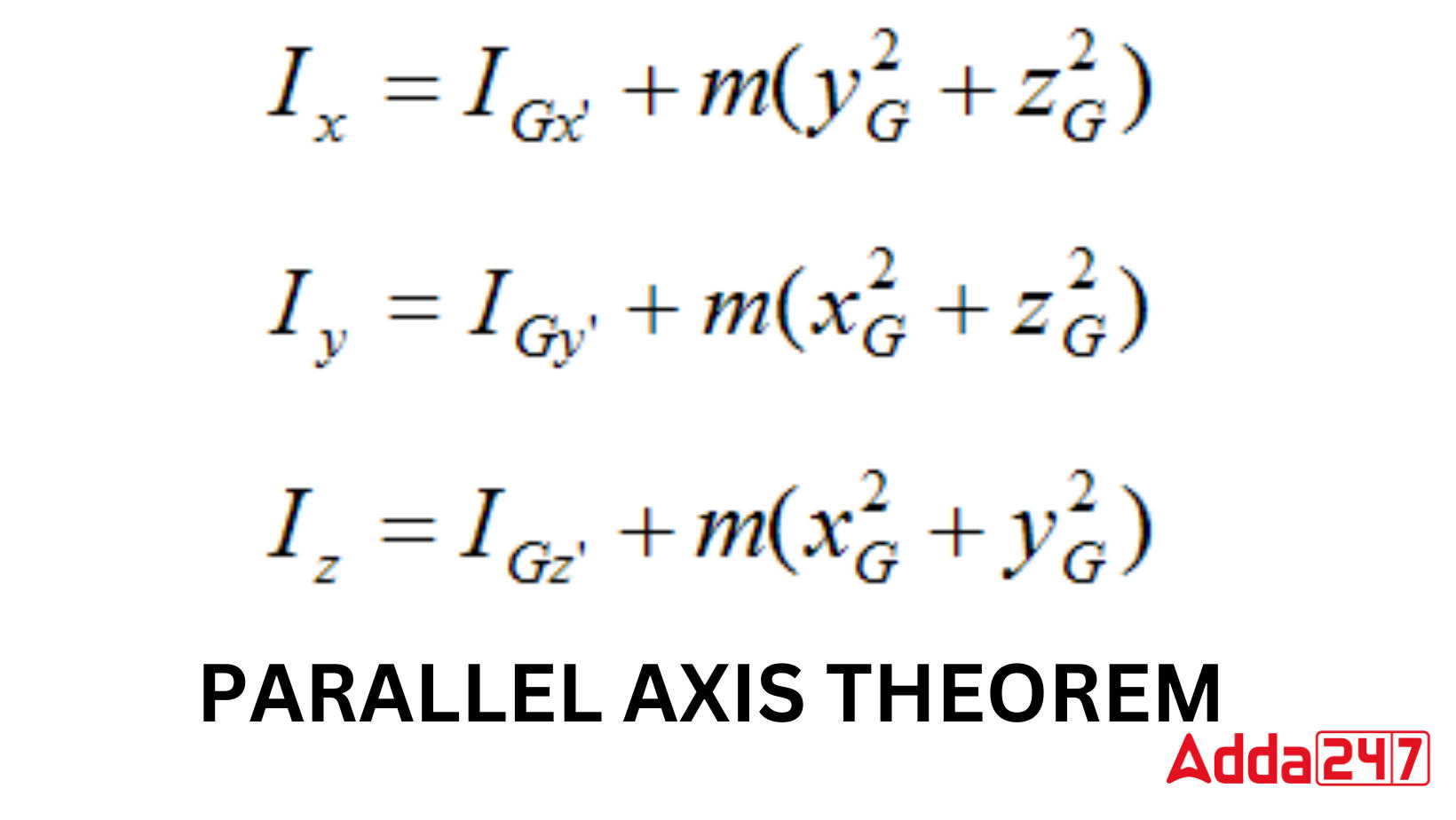

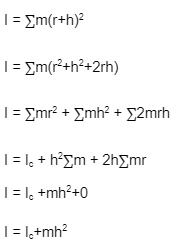








 MGSU Result 2025 Out, Download Maharaja ...
MGSU Result 2025 Out, Download Maharaja ...
 EMS Results 2025 OUT at gnanasangama.kar...
EMS Results 2025 OUT at gnanasangama.kar...
 How to Calculate CUET Score, Check Marks...
How to Calculate CUET Score, Check Marks...









