What is the Definition of Mean?
Mean is the average of all the set of numbers which is used to get the result between the number of numbers. It is calculated by adding together all the numbers in a set and then dividing by the number of items in that set.
Mean Meaning
Mean is also known as arithmetic mean or mathematical average. Calculating the average from a set of numbers requires at least 2 numbers. This form of average is widely used in both scientific calculation and statistical notation.
The mean is a useful tool for understanding and analyzing data sets. It is often used in statistical analysis and in mathematical modeling. The mean can help you to identify trends and patterns in data sets.
Mean Formula Class 10
Now we know that to get the result from a data set, we should use the following formula. In which first all the numbers given in the data set are summed and it is divided by the number of items given in the data set. So now let’s understand it through an example –
if you wanted to find out the mean for 4, 5, 6, 3, and 7 first add up all values (4 + 5 + 6 + 3 + 7 = 25) and then divide that sum by the number of items (25/5 = 5). The answer would be an average or mean value; in this case it would be 5.
Mean Symbol
The symbol for the mean is usually given as x-bar, or x̄.
Examples of its usage in everyday life include a cricketer’s average number of runs scored in test matches, as well as the mean price of houses in certain geographic areas as estimated by real estate agents.
Formula of Mean- Formula for Mean
The mean is the average of a set of numbers, and is often used as a measure of central tendency. The formula for mean is very simple: add up all the numbers in a set, and then divide by the total number of values in the set. formula of mean is given below.
Mean = Sum of the number given in Data/ Total number given in Data
Example Question – Find the mean of first 5 prime Number.
Solution – First 5 prime number is – 1,2,3,4,5
Using formula – (1+2+3+4+5) / 5 =
15/5 = 3 Ans.
How to Find Mean?
This page focuses on two types of mean formula in statistics: those employed when data is ungrouped and those used when data is grouped. As a refresher, the mean formula for ungrouped data is the sum of all observations divided by the number of observations; however, the formula changes when the data is categorized. Let’s dive right into our exploration!
Mean Formula for Ungrouped Data
Given n observed values x1, x2, x3…xn, the mean of these values can be calculated as follows:
The formula for the ungrouped data mean is the same as the formula for the ordinary mean. But if we want to write it with mean symbol, then we will write this formula like this –
x̄=∑ x/n
Example Question – Find the mean of the following data: 10, 15, 12, 16, 15, 10, 14, 15, 12, 10.
Solution:
Using Formula = (10+15+12+16+15+10+14+15+12+10) / 10
= 129/10
= 12.9
Mean Formula for Grouped Data
For large data sets, a frequency distribution table is a useful way to organize the values. This type of table provides information about the value and its frequency – that is, how many times each value appears in the dataset. For discrete frequency distributions, there are several methods for computing the arithmetic mean.
| Method | Formula |
| Direct method | Direct method of mean formula x̄ = Σfixi/Σfi |
| Shortcut method | Mean x̄ = A + ∑fidi/∑fi |
| Step-Deviation method | Mean x̄ = A + h (∑fiui / ∑fi) |
Types of Mean in Maths
There are 3 types of Mean which is important in Mathematics –
- Arithmetic Mean
- Geometric Mean
- Harmonic Mean
1. Arithmetic Mean
Arithmetic Mean is an important method for calculating the central tendency of a given dataset. It takes into account all of the data points in the set and can have any sign – positive, negative, or zero.
There are two types of Arithmetic Mean: the sample mean and the population mean. The sample mean divides the sum of a set of observations by their count and indicates the centrality of that particular data set;
whereas, the population mean divides total observations by its size in order to ascertain a group’s overall characterizing middle value.
Formula of Arithmetic Mean is – x̄ = Σxi/n (or) x̄ = Σfixi / Σfi
2. Geometric Mean
The geometric mean is used to find the nth root of the product of n numbers from the given data. You can find the nth root of a given number by multiplying it through the geometric mean. For example, if you have three numbers X, Y, Z, then their geometric mean will be 3 XYZ.
Formula of Geometric Mean is – x̄ = n√(x1 · x2 · x3 · … · xn)
Example – Geometric mean of 4 and 2 = √4 x 2 = 2√2
3. Harmonic Mean
Harmonics Mean is a powerful way to analyze data. It is used to find the average ratio. This makes it especially useful in time and average analysis, as well as in any situation where large or small numbers would impact the analysis results.
Let there be two numbers X and Y, for which the harmonic mean will be 2xy(x+y) and for the same three numbers X, Y and Z the harmonic mean will be 3xyz(xy+xz+yz).
Formula of Harmonic Mean is – x̄ = 1/[Σ(1/xi)]/N = N/Σ(1/xi)
What are the Benefits of Learning Mean in Statistics?
We often see that whenever we add any number in mathematics and divide it by the total number of data, then we call it average. But in statistics, the method of calculating this average is called mean. Because in mathematics there is only one formula to find the average, while in statistics there are many formulas and also in many different ways this average can be found.
So, there are many advantages to learning the Mean in statistics.
- The Mean is a very important concept in statistics, and it is used in a wide variety of applications.
- Learning the Mean can help you to better understand data and to make more informed decisions.
- The Mean is also a very useful tool for analyzing data.
- In addition, the Mean is a very important concept in statistics, and it is used in a wide variety of applications.
- By calculating the Mean of each data set, you can easily compare their central tendencies and determine if there are any significant differences between them.

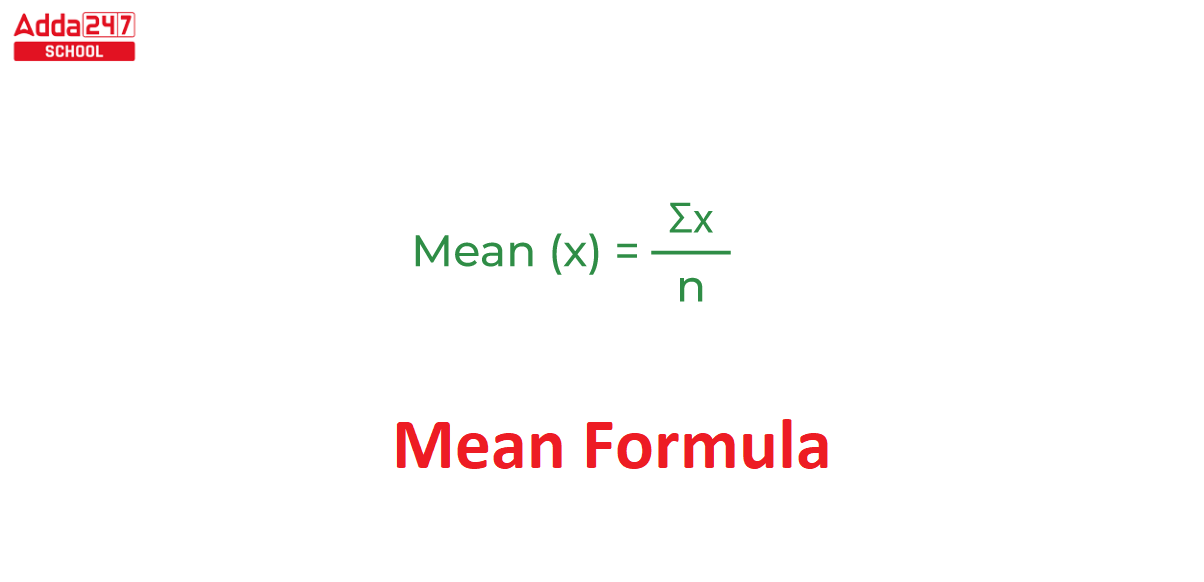







 CUET UG Final Answer Key 2025 Revised, D...
CUET UG Final Answer Key 2025 Revised, D...
 DU Cut off 2025, Delhi University Expect...
DU Cut off 2025, Delhi University Expect...
 OUAT Result 2025 OUT @ouat.nic.in: Check...
OUAT Result 2025 OUT @ouat.nic.in: Check...









