Magnetic Field Formula: A magnetic field can be created by a current, an electrically charged particle movement, or a magnetized material. In other words, a magnetic field is a region surrounding a magnetic material or an electric charge in motion where the force of magnetism operates. A magnetic force is felt by the pole of a magnet, a current-carrying wire, or charged particles that travel in a magnetic field. Furthermore, the magnetic field’s direction is determined by the current’s direction. The magnetic flux density is the strength of the magnetic field at a given place in space, and it is expressed in tesla (T). Discover more about the magnetic field, the magnetic field formula, its derivation, and intensity in this article.
Magnetic Field Definition
What is Magnetic Field ? We’ve all observed how magnets on the same side attract each other since we were kids. This magnetic field, however, is distinct; it is the field generated by electricity that draws and repels the magnet. A magnetic field is a vector field in the vicinity of a magnet, electric current, or fluctuating electric field that exhibits magnetic forces. The magnetic field is a tool that we use to describe how magnetic force is dispersed in the space surrounding and within anything magnetic in character.
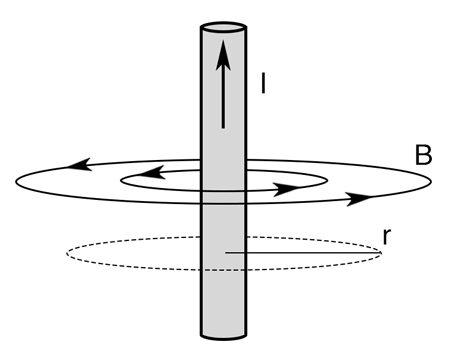
Magnetic Field Formula
Right-hand rule: we can use the ‘right-hand rule’ to determine the direction of the Magnetic Field. By pointing the thumb of your right hand towards the direction of the current. Furthermore, the magnetic field aligns up with the direction of your curled fingers. The magnitude of the magnetic filed is determined by the quantity of current and the distance from the charge-carrying wire.
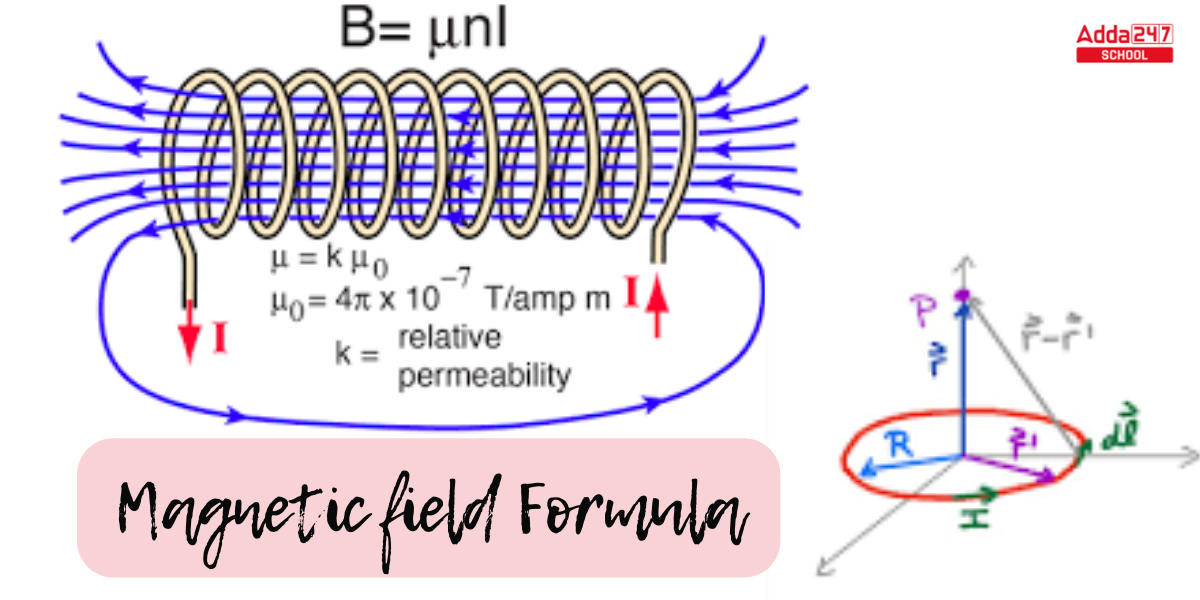
The constantμ0 appears in the magnetic field formula, is referred to as free space permeability and has a valueμ0 = 4π×10−7(T⋅m/ A).
A magnetic field is also measured in Tesla (T).
B = denotes the magnitude of the magnetic field in Tesla (T).
μ0 = refers to the open space permeability (4π×10−7T⋅m/A).
I = The magnitude of the electric current in amperes (A) is denoted by I.
r = distance in meters (m)
How a Magnetic Field created?
When a charge moves, it creates a magnetic field around it. There are two fundamental approaches to setting a charge in motion and producing an effective magnetic field. The Magnetic Field generated by a Current-Carrying Conductor is explained here.
How A magnetic field is produced by a current-carrying conductor?
Ampere proposed that a magnetic field is created anytime an electrical charge moves.
- Consider an electrical cable/ wire that is connected to a battery and through which current is made to flow. As the current across the conductor increases, so does the magnetic field. The magnetic field diminishes with distance as we travel away from the wire.
- This can be described using Ampere’s law. The equation yields the magnetic field at some distance r from a long current-carrying conductor I, in accordance with the law. The permeability of open space (µ0=4π×10-7 T⋅ m/A) is a particular constant in the equation.
- Magnetic fields can be concentrated in materials having higher permeability.
- Because the magnetic field is a vector quantity, it possesses a direction. The right-hand rule can be used to calculate the conventional current travelling through a straight wire.
Magnetic Field Formula for Circular Coil Examples
The Biot-Savart law can be used to calculate the magnetic field caused by a current. We first investigate arbitrary sections on opposite sides of the loop to prove qualitatively that the net magnetic field vector is along the central axis of the loop using vector findings. The magnetic field expression can then be derived using the Biot-Savart law.
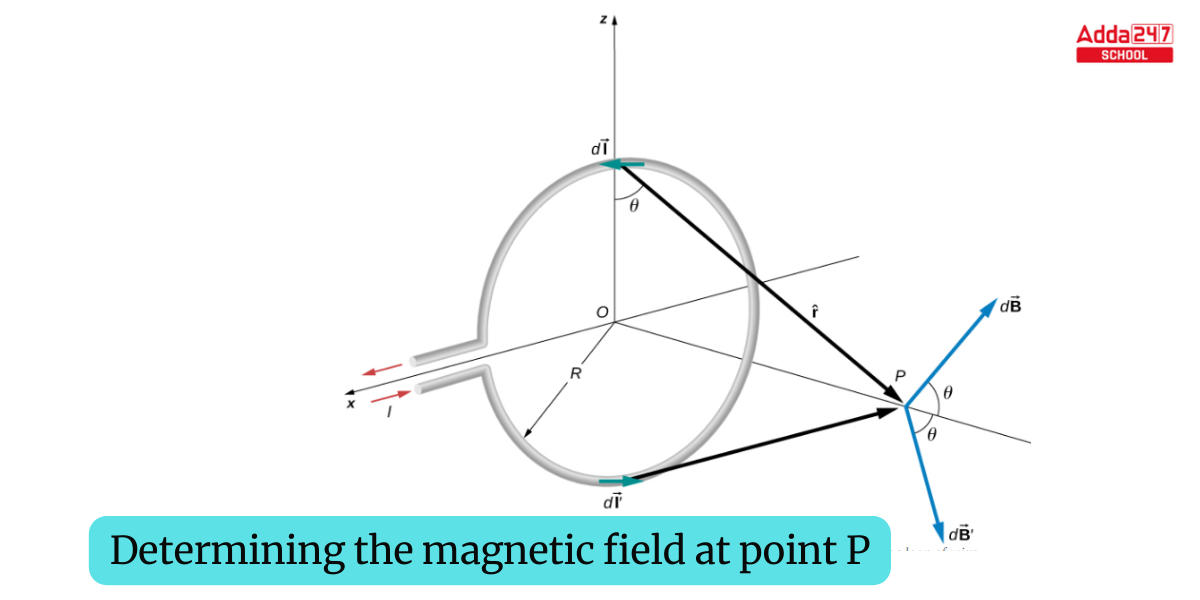
Let P be the distance y from the loop’s center. The magnetic field
at P, created by the current element Id
, is oriented at an angle over the y-axis as given by the right-hand rule. Because d
is parallel to the x-axis and
is in the yz-plane, the two vectors are parallel to one another, resulting in
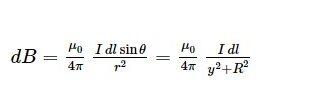 where ,
where , 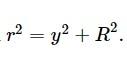
Considering the magnetic field
caused by the current element I
, which is located precisely opposite Id
on the loop. Equationabove also gives the magnitude of
, but it is pointed at an angle below the y-axis. As a result, the components of d and
perpendicular to the y-axis cancel, and only those that run along the y-axis must be considered for computing the net magnetic field. In pairs, the components perpendicular to the loop’s axis add to zero. As a result, at point P:
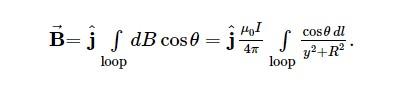
y, R, and cosθ are constant for all
elements on the wire and are connected by
.
The magnetic field at P is,
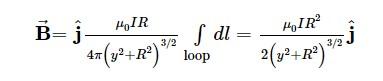
where we used 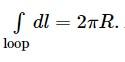
The closed current loop, as discussed in the preceding chapter, is a magnetic dipole of moment-![]() In this case,
In this case,
and
=
, therefore the magnetic field at P can be written as
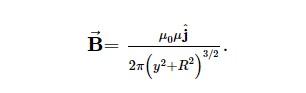
Setting y=0 in Equation yields the magnetic field at the loop’s centre:
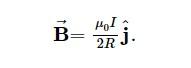 For a flat coil with n loops per length, this equation becomes
For a flat coil with n loops per length, this equation becomes ![]() It can also be written as
It can also be written as
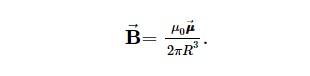 When we examine y>>R in Equation, the statement is reduced to the magnetic field from a dipole –
When we examine y>>R in Equation, the statement is reduced to the magnetic field from a dipole –
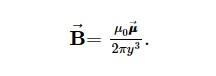
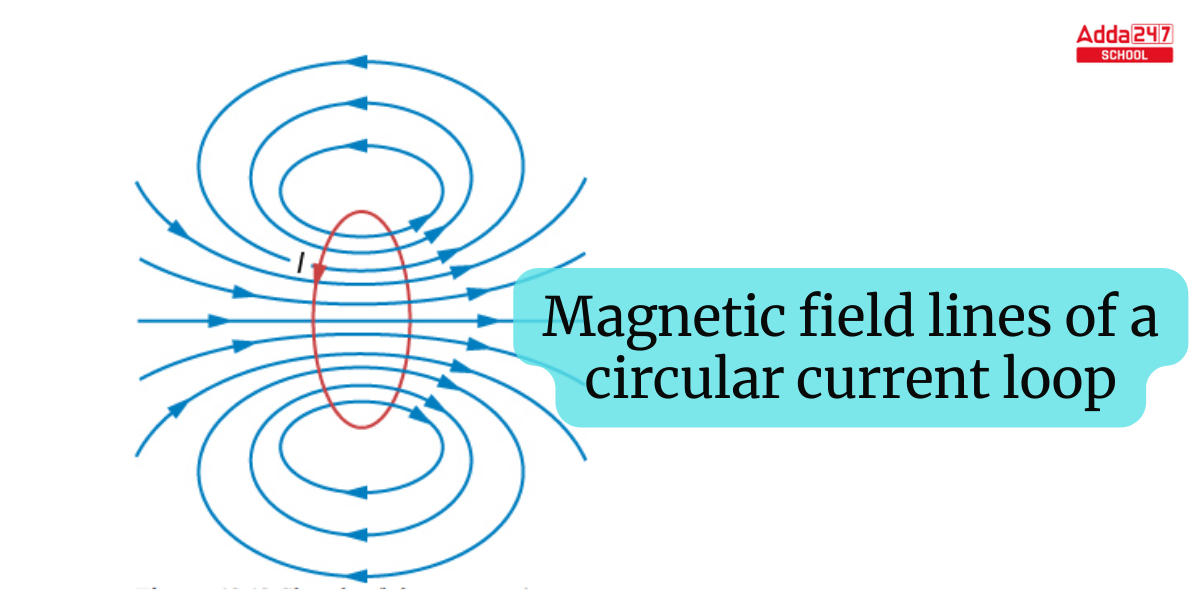
The magnetic field owing to the circular current loop at off-axis sites involves somewhat difficult maths, so we’ll just look at the findings. The magnetic field lines are illustrated in the figure below. Take note of how one field line parallels the loop’s axis. This is the field line that we just discovered.
Intensity of Magnetic Field
The force endured by the unit north pole at any point in the magnetic field can be described as magnetic field intensity (H). In basic terms, it is an indication of the strength or weakness of any magnetic field. Tesla is the SI unit for measuring magnetic field intensity. A Tesla magnetic field is defined as one newton of force per ampere of current per meter of conductor. It can also be expressed as amperes / meter.
It is calculated using the Magnetic Field Intensity formula H = B/μ – M
where, B represents the magnetic flux density
M stands for magnetization.
μ is a measure of magnetic permeability
Magnetic Field Equations
Magnetic field equations describe the behavior of magnetic fields in various situations. The most fundamental equations that govern magnetic fields are Maxwell’s equations, which are a set of four equations that describe the fundamental principles of electromagnetic theory. These equations were formulated by James Clerk Maxwell in the 19th century and are crucial in understanding the behavior of electric and magnetic fields.
Here are Maxwell’s equations, including the two equations specifically related to the magnetic field:
- Gauss’s Law for Electricity: ∇ ⋅ E = ρ / ε₀This equation states that the divergence of the electric field (E) at a point in space is equal to the charge density (ρ) at that point divided by the permittivity of free space (ε₀).
- Gauss’s Law for Magnetism: ∇ ⋅ B = 0Gauss’s Law for magnetism states that the divergence of the magnetic field (B) at a point in space is always zero, which means there are no magnetic monopoles (individual north or south magnetic charges).
- Faraday’s Law of Electromagnetic Induction: ∇ × E = -∂B/∂tThis equation describes how a changing magnetic field induces an electric field. The curl of the electric field (E) is equal to the negative rate of change of the magnetic field (B) with respect to time (t).
- Ampère’s Law with Maxwell’s Addition: ∇ × B = μ₀J + μ₀ε₀∂E/∂tAmpère’s law describes how a current (J) generates a magnetic field. Maxwell added the second term on the right, which accounts for the displacement current (ε₀∂E/∂t), allowing the equation to be consistent with the conservation of electric charge and the changing electric field.
In these equations:
- E represents the electric field vector.
- B represents the magnetic field vector.
- ∇ ⋅ denotes the divergence operator.
- ∇ × denotes the curl operator.
- ρ is the charge density.
- ε₀ is the permittivity of free space.
- μ₀ is the permeability of free space.
- ∂/∂t represents the partial derivative with respect to time.
These equations form the foundation for understanding how magnetic fields interact with electric fields, charges, currents, and changing electric fields in a wide range of electromagnetic phenomena. They are essential in the study of electromagnetism and are used extensively in physics and engineering to analyze and design various devices and systems involving electromagnetic fields.








 HPBOSE Compartment Date Sheet 2025 Out, ...
HPBOSE Compartment Date Sheet 2025 Out, ...
 RUHS Counselling 2025 Round 1 Seat Allot...
RUHS Counselling 2025 Round 1 Seat Allot...
 Bihar Board Dummy Registration Card 2026...
Bihar Board Dummy Registration Card 2026...










