lcm Full Form in Maths with Examples

Table of Contents

LCM Full Form- Least Common Multiple

The Least Common Multiple is the meaning of the acronym LCM. The lowest number that may be divided by both numbers is known as the least common multiple (LCM) of two numbers. It can also be computed using two or more numbers. Finding the LCM of a given collection of numbers can be done in a variety of ways. Utilizing the prime factorization of each number and then calculating the product of the greatest powers of the shared prime factors is one of the quickest techniques to determine the LCM of two numbers.

LCM Full Form in Maths

In mathematics LCM full form is, the least common multiple is sometimes referred to as LCM or the lowest common multiple. The smallest number among all the common multiples of the provided numbers is the least common multiple of two or more numbers. Consider the integers 2 and 5. There will be different multiples for each.

2, 4, 6, 8, 10, 12, 14, 16, 18, and 20 are all multiples of 2.

5, 10, 15, 20, etc. are all multiples of 5.

Full Form of LCM: How to find LCM?

The full form of lcm is the least common multiple. There are several ways to calculate the LCM of a set of numbers. The least common multiple of two numbers can be found using one of three techniques. Below are explanations of each technique with examples.

LCM by the Listing method
LCM by Prime Factorization Method
LCM by Division Method

Find LCM by Listing Method

By listing the multiples of two or more numbers, we can determine the common multiples of those numbers. The least common multiple among these frequent multiples is taken into account, allowing the LCM of two supplied values to be determined. The procedures shown below are used to determine the LCM of the two numbers A and B using the listing approach.

List the first several multiples of A and B in step one.
Mark the multiples of both numbers that are common to both.
Choose the least common multiple in step three.
The LCM of the two numbers is the lowest common multiple.

Questions and Answers: Find the least common multiple (LCM) of 3 and 6

Solution: The first few multiples of 3 are 3,6,9,12 etc.

The first few multiples of 6 are 6.12.18 etc.

We can observe that 6 is the least common multiple of 3 and 6. So, LCM of 3 and 6 is 6.

Find LCM by Prime Factorization Method

The LCM of the given numbers can be determined by applying the prime factorization method. The following steps are used to determine the LCM of two numbers using the prime factorization method:

Step 1: Use the repeated division method to identify the prime factors of the given numbers.

Step 2: Write the numbers in exponent form in step two. Only those prime factors’ product with the highest power should be sought.

Step 3: The LCM of the provided numbers is the product of these factors with the highest powers.

Let’s use the example below to learn this method.

Questions and Answers: Find the least common multiple (LCM) of 20 and 40 using prime factorization.

Solution:

Let us find the LCM of 60 and 90 using the prime factorization method.

Step 1: The prime factorization of 60 and 90 are: 60 = 2 × 2 × 3 × 5 and 90 = 2 × 3 × 3 × 5
Step 2: If we write these prime factors in their exponent form it will be expressed as, 60 = 2² × 3¹ × 5¹ and 90 = 2¹ × 3² × 5¹
Step 3: Now, we will find the product of only those factors that have the highest powers among these. This will be, 2² × 3² × 5¹ = 4 × 9 × 5 = 180

Therefore, LCM of 60 and 90 is 180.

Find LCM by Division Method

By dividing the integers by a common prime number, we may determine the LCM by the division method. The LCM of the resulting prime factors is then calculated. Let’s examine this approach utilising the following steps:

Step 1 is to identify a prime number that at least one of the given numbers can be factored into. To the left of the provided numbers, write this prime number.

Step 2: Divide the number by the prime and write the quotient below it if the prime number from step 1 is a factor of the number. Write the number in the row below as it is if the prime number from step 1 is not a factor of the number. Continue the steps until 1 is left in the last row.

Let us understand with the given example.

For example: Find the least common multiple (LCM) of 6 and 15 using the division method.

Solution: Let us find the least common multiple (LCM) of 6 and 15 using the division method using the steps given below.

Step 1: 2 is the smallest prime number and it is a factor of 6. Write 2 on the left of the two numbers. For each number in the right column, continue finding out prime numbers which are their factors.
Step 2: 2 divides 6 but it is not a factor of 15, so we write the number 15 in the row below as it is. Continue the steps until 1 is left in the last row. Then, we divide 3 and 15 by 3. This gives us 1 and 3. Now, again we write 5 on the left side and we finally get 1, 1 as the quotient in the last row.
Step 3: Then we multiply these numbers on the left. The LCM is the product of all these prime numbers. LCM of 6 and 15 is, 2 × 3 × 5 = 30.

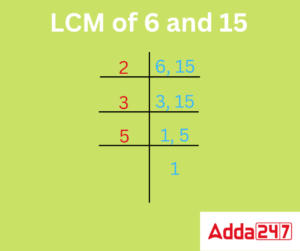
Despite the fact that there are three ways to find the least common multiple, the division technique is the most popular and straightforward.

Difference between LCM and HCF

The LCM, or least common multiple of two or more numbers, is the smallest number among all the common multiples of the provided numbers, whereas the HCF, or highest common factor of two or more numbers, is the highest or the biggest factor among all the common factors of the given numbers. The following table illustrates how HCF and LCM differ from one another:

LCM (Lowest Common Multiple)	HCF (Highest Common Factor)
The least common multiple of two or more numbers is the smallest number among all common multiples of the given numbers.	The highest common factor of two or more numbers is the highest number among all the common factors of the given numbers.
LCM of two or more prime numbers is always the product of those numbers.	HCF of two or more prime numbers is 1 always.
LCM of two or more numbers is always greater than or equal to each of the numbers.	HCF of two or more numbers is always less than or equal to each of the numbers.

LCM Full Form in Maths with Examples- QNAs

Que. How do we calculate LCM?

Ans. There are several ways to calculate the LCM of a set of numbers. The least common multiple of two numbers can be found using one of three techniques. Like Listing method, Prime factorisation or division method.

Que. What is the LCM example?

Ans. LCM denotes the least common factor or multiple of any two or more given integers. For example, L.C.M of 16 and 20 will be 2 x 2 x 2 x 2 x 5 = 80, where 80 is the smallest common multiple for numbers 16 and 20.

Que. What is the LCM of 12 and 16?

Ans. The LCM of 12 and 16 is 48.