HCF- Highest Common Factor, Formula, Definition and Examples

Q: Que. What is the full form of HCF?

Ans. The full form of HCF is the Highest Common Factor

Q: Que. How do you calculate the HCF?

The highest common factor (HCF) is found by finding all common factors of two numbers and selecting the largest one.

Table of Contents

HCF- Highest Common Factor

HCF, or the highest common factor, is the number that divides each of the two or more numbers most evenly. The Greatest Common Measure (GCM) and Greatest Common Divisor (GCD) are further names for HCF. The least common multiple, or LCM, is used to determine the smallest common multiple of any two or more numbers. LCM and HCM are two separate methods.

What is HCF?- Definition

HCF is the short form of the Highest Common Factor. The highest factor that may divide two integers evenly is known as the HCF of two numbers. HCF can be assessed using two or more numbers. It is the most powerful divisor for any pair of integers that can divide the inputted numbers equally or fully.

For example, The highest common factor of 24 and 36 is 12 because 12 is the largest number which can divide both 24 and 36 exactly.

How to find HCF?

There are two ways we can determine the HCF of any given set of numbers:

using the prime factorization method
with the division method

In this essay, let’s explore each of these two methods separately.

HCF by Prime Factorization Method

To use the prime factorization method to determine the HCF of numbers, follow the steps below.

Step 1: Write each integer as the sum of its prime factors in step one. Prime factorization is the term used for this technique.

Step 2: List the elements that both numbers have in common.

Step 3: The HCF is the sum of all the common prime factors ( use the lower power of each common factor)

Let’s use examples to better understand.

Example 1: Evaluate the HCF OF 60 and 75

Solution:

Write each number as a product of its prime factors.2²x 3 x 5 = 60

3 x 5²= 75

The product of all common prime factors is the HCF.

The common prime factors in this example are 3 & 5.

The lowest power of 3 is 3 and 5 is 5.

So, HCF = 3 x 5 = 15

Example 2: Evaluate the HCF OF 36,24 and 12

Solution:

Write each number as a product of its prime factors.2²x 3² = 36

2³ x 3 = 24

2²x 3 = 12

The product of all common prime factors is the HCF ( use the lowest power of each common factor)

The common prime factors in this example are 2 & 3.

The lowest power of 2 is 2² and 3 is 3.

So, HCF = 2² x 3 = 12

HCF by Division Method

You now learn how to use prime factorization to determine the highest common factor. Let’s now examine how to calculate HCF using the division approach. The division method basically consists of dividing the provided integers simultaneously to find their common factors. To address the HCF difficulties, adhere to the instructions listed below.

Step 1: Write the given numbers horizontally in order, using commas to separate them.
Step 2: Find the smallest prime number that can divide the supplied number in step two. It must divide the given numbers precisely. (Fill in the left-hand side.)
Step 3: Write the quotients now.
Step 4: Keep going through the process until there are no more coprime numbers.
Step 5: Since the factors on the left-hand side evenly divide each integer, we will get the common prime factors. The HCF of the specified numbers is the sum of these usual prime factors.

With the help of some examples, let’s better learn how to use the division method to obtain the HCF.

Example 1: Evaluate the HCF of 30 and 75

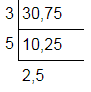
As we can see, the prime factors listed on the left side split all of the numbers perfectly. They are therefore all common prime factors. The remaining numbers at the bottom don’t have a common prime factor.

So, HCF = 3 × 5 = 15.

Example 2: Find out HCF of 36, and 24

HCF = 2 × 2 × 3 = 12.

Example 3: Find out HCF of 36, 12, 24 and 48.

HCF = 2 × 2 × 3 = 12.

HCF by Shortcut method

Steps for calculating the HCF of any given set of numbers.

Step 1 is to first divide the greater number by the smaller number, as in;

Greater/smaller numbers

Step 2: Subtract the remainder from the step 1 divisor.

Step 1/Remainder divisor

Step 3: Subtract the residual from the step 2 divisor once more.

Step 2/Remainder divisor

Step 4: Carry on until there is no more number left over.
Step 5: The HCF is the divisor of the previous step.

How to find the HCF of Three numbers

Look at the steps to calculate the HCF of the 3 numbers given in the question.

1) Calculate the HCF of 2 numbers.

2) Then Find the HCF of the 3rd number and the HCF found in step 1.

3) The HCF you got in step 2 will be the HCF of the 3 numbers.

The above steps can also be used to find the HCF of more than 3 numbers.

HCF of Four Numbers

To determine the HCF of 4 digits, follow these easy steps:

Separate the four digits into pairs of two first.
Find the HCF of two numbers in a pair.
Next, determine the HCF of the HCFs that were calculated in step one.
The required HCF of 4 numbers will be the final HCF.

HCF of Prime Numbers

Any two or prime numbers have an HCF that is always equal to 1.

Why?

Due to the fact that prime numbers only have two factors—either 1 or the number itself. Therefore, the HCF of such numbers will be equal to 1 if there is no additional component. Look at the following examples:

HCF (2, 3),
HCF (3, 7),
HCF (5, 13),
HCF (19, 23) all equal one.

Properties of HCF

When two or more numbers are given, the HCF of those numbers divides the numbers exactly.
The HCF of prime numbers is always equal to one
HCF is always less than or equal to the numbers given.

Solved Question on HCF

Q.1: Determine the plank length that can be utilised to measure the given values of length 4 m 50 cm, 9 m 90 cm and 16 m 20 cm in the limited time period.

Answer:

On conversion of length to centimeters,

4 m 50 cm = 450 cm

9 m 90 cm = 990 cm

16 m 20 cm = 1620 cm

To determine the length of the sizeable plank that can be utilised to measure the given values of length in a limited time period, the highest common factor needs to be taken.

450 = 2 × 3 × 3 × 5 × 5 = 2 × 3² × 5²

990 = 2 × 3 × 3 × 5 × 11 = 2 × 3² × 5 × 11

1620 = 2 × 2 × 3 × 3 × 3 × 3 × 5 = 2² × 3⁴ × 5

HCF (450, 990, 1620) = 2 × 3 × 3 × 5 = 90

Q.2: Determine the largest number on dividing 70 and 50 leaves behind remainders one and four.

Answer:

The essential digit leaves behind remainders one and four on dividing 70 and 50.

The numbers 69 and 46 are obtained.

To determine the HCF 69 (3 × 23) and 46 (2 × 23).

The highest common factor (HCF) of 69 and 46 is 23.

Q.3: Determine the greatest number that divides 64, 136 and 238 and leaves behind the same remainder in every case.

Answer:

To determine the required number, the highest common factor of (136 – 64), (238 – 136) and (238 – 64) that is the HCF (72, 102, 174) needs to be found.

72 = 2³ × 3²

102 = 2 × 3 × 17

174 = 2 × 3 × 29

HCF (72, 102, 174) = 2 × 3 = 6

6 is the required number.

Q.4: Find the highest count of students among whom 182 chocolates and 247 candies can be given such that every student obtains the same count of each. Also, what is the count of the chocolates and candies every student will obtain?

Answer:

The value of HCF of the count of chocolates and candies that needs to be found gives the count of the students.

HCF (182, 247) = 13

13 students.

Count of chocolates for every student = 182/13 = 14

Count of candies for every student = 247/13 = 19

For more knowledge, download the Adda247 App

Found this article helpful?

Reach us by means of a visit or call our senior instructor at +91-9625869989 to figure out additional information about the various choices and streams that are open.

We would really see the value in it on the off chance that you could grant a portion of your insight. By utilizing our application, tests, and YouTube class help, you can unwind any vulnerability assuming that you’re centered around getting the best grades Adda247.

FAQs on HCF

Que. What is the full form of HCF?

Ans. The full form of HCF is the Highest Common Factor

Que. How do you calculate the HCF?

Ans. The highest common factor (HCF) is found by finding all common factors of two numbers and selecting the largest one.

Que. What is HCF and LCM?

Ans.The full form of LCM in Maths is the Least Common Multiple and the full form of HCF is the Highest Common Factor.

Que. What is HCF example?

Ans. HCF can be evaluated for two or more than two numbers. It is the greatest divisor for any two or more numbers, that can equally or completely divide the given numbers.