One of the most often-used mathematical formulas is the average formula, particularly in the context of quantitative operations. In mathematics, an average is a number figure that is used to represent a huge amount of data. As a result, the average value is used since it helps to express all of the values in a single value. Check here Average All Formulas in Maths.
Average Definition
The average term is used frequently in general conversations as well as in Mathematics. You must note that the meaning of term average is same in all the cases. Let us understand the definition of average.
“average is to determine the mean or center value of a set of data”
The average is easily estimated by adding all of the data values and dividing them by the number of elements. In this article, we are going to learn about the Average Formula, and how to calculate the average along with solved examples in this post.
What is Average?
In mathematics, an average of a set of data is the expression of the set’s center value. It is defined mathematically as the ratio of the sum of all the data to the number of units in the list. The average value of a group of integers is the computed “central” value in mathematics. The middle or ‘center’ point is referred to as the ‘average’. Understanding averages helps us handle vast volumes of data more effectively and has many practical uses.
Average Formula in Maths
The definition of average is to determine the mean or center value of a set of data.The Formula is widely used to determine the center value. It is fairly simple to calculate the average of a set of numbers or values using the average formula. By adding up all the data values and dividing them by the total number of items, it is simple to determine the average. As a result, the following is the mathematic avg formula:
Average formula = Sum of Values/ Number of values
Suppose, we have given with n number of values such as x1, x2, x3 ,….., xn. The average or the mean of the given data will be equal to:
Average = (x1+x2+x3+…+xn)/n
For Example, The average of 5, 10, 12. 18. and 35 is (5+10+12+18+35)/5= 80/5 = 16. As a result, the average of the given number set is 16.
How to Calculate Average with the Formula?
Using the Average formula we can easily find out the mean or central value for a given set of variables is simple to compute. We only need to follow the steps below when computing the Average.
Step 1: The first step in calculating the average of numbers is to add all of the given numbers together.
Step 2: Next, we must count the number of numbers in the given dataset.
Step 3: Utilize the Avg. formula to determine the outcome. Divide the sum by the number of observations to get the average. The formula for calculating the average of a number is:
Average = Sum of the Observations / Number of Observations.
Arithmetic Mean Symbol
The arithmetic mean is also known as the mean or arithmetic average. It is calculated by summing all of the numbers in a given data set and then dividing the total number of items in that set by the total number of items in that set. The arithmetic mean is nothing but the ratio of the total number of observations to the sum of all provided observations.
For Example, A given number set with n integers, each symbolized by ai (where i = 1,2,…, n), the arithmetic mean is the total of the as divided by n, then:
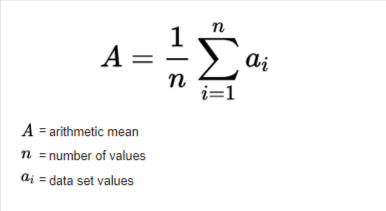
Geometric Mean
The geometric mean is a way to determine the average of a group of numbers by taking the nth root of the multiplication of n numbers. It is a completely different concept from the arithmetic mean, as we add up all the observations and then divide the total by the number of observations. However, in the geometric mean, we multiply all the observations together and then take the nth root of the product, where n represents the number of observations.
Harmonic Mean
The harmonic mean is calculated by taking the reciprocal of the average of the reciprocals of the data values provided. The harmonic mean can be calculated using the following formula:
The Harmonic Mean is represented by the formula HM = n / [(1/x1)+(1/x2)+(1/x3)+…+(1/xn)].
x1, x2, x3,…, xn represent the distinct elements within a total of n items.
Average All Formulas
Average-based problems appear frequently in both Board Exams and Competitive Exams. Students can use the following formulas to answer problems about averages:
| Average Formulas List | |
| Avg. formula of first n natural numbers | (n+1) / 2 |
| Average of first n even numbers | n + 1 |
| Average of first n odd numbers | n |
| Average of squares of first n even numbers | (n+1) (2n+1) / 6 |
| Average of squares of first n natural numbers | n (n+1)2 / 4 |
| Average of squares of first n odd numbers | (2n+1) (2n-1) / 3 |
| Average of cube of first n even numbers | 2n (n+1)2 |
| Average of cube of first n odd numbers | n(2n²– 1) |
| Average of cubes of first n natural numbers | n (n+1)2 / 4 |
Average all Formula PDF Content
Here we give average all formula pdf content for Students who are preparing for Class 10 and 12 Board Exams.
1. Average = (Total of data) / (No. of data)
2. Age of New Entrant = New Average + No. of Old Members * Increase
3. Weight of New Person = Weight of Removed Person + No. Of Persons *
Increase In Average
4. Number of Passed Candidates = Total Candidates * (Total Average – Failed
Average) / (Passed Average – Failed Average)
5. Number of Failed Candidates = Total Candidates * (Passed Average – Total
Average) / (Passed Average – Failed Average)
6. Age of New Person = Age of Removed Person – No. of Persons * Decrease in
Average Age
7. Average after x innings = Total Score – Increment in Average * y innings
8. If a person travels a distance at a speed of x km/hr and the same distance at a
speed of y km/hr, then the average speed during the whole journey is given by
– 2xy / (x+y) km/hr.
9. If half of the journey is travelled at a speed of x km/hr and the next half at a
speed of y km/hr, then average speed during the whole journey is 2xy / (x+y)
km/hr.
10. If a man goes to a certain place at a speed of x km/hr and returns to the
original place at a speed of y km/hr, then the average speed during up and
down journey is 2xy / (x+y) km/hr.
11. If a person travels 3 equal distances at a speed of x km/hr, y km/hr and z
km/hr respectively, then the average speed during the whole journey is 3xyz /
(xy+yz+zx) km/hr.
12. If decrease in average = x
Increase in expenditure = y
Increase in no. of students = z
And number of students (originally) = N, then
The original expenditure = N * [ x*(N+z) + y ] / z ]
Maths Average Formula Examples
Example 1: Calculate the average of 10, 13, 22,45, and 60.
Solution: Sum of the all given numbers = 10+ 13 + 22 + 45 + 60 = 150
In the given Number set there, a is a total of 5 no present.
Average formula = Sum of Values/ Number of values
The Average of the Given Number set is = 150/5 = 30
Example 2: If the weights of the 7 students in a group are 42, 50, 38, 36,47,44, 37. Then, determine the average weight of the students in that group
Solution:
The students’ ages are 42, 50, 38, 36,47,44, and 37.
Using the Avg. formula we can say that, Average = Sum of Values/ Number of Students.
In the given problem, the Sum of 7 students’ wright is (42+50+38+36+47+44+37)=294
Total number of members in this Group =7
Average = 294/7= 42.
As a result, the average weight of students in the group is 42 years.
Example 3: Average of a Set of Numbers
Problem: Find the average of the numbers 5, 10, 15, and 20.
Solution:
Sum of values:
5+10+15+20=50
Number of values:
4
Average:
50/4= 12.5
Example 4: Average of Test Scores
Problem: A student scores 80, 85, 90, and 95 on four tests. What is the average score?
Solution:
Sum of scores:
80+85+90+95=350
Number of tests:
4
Average:
350 /4 = 87.5
Example 5: Average Speed
Problem: A car travels 60 km in 1 hour, 90 km in 1.5 hours, and 120 km in 2 hours. What is the average speed of the car?
Solution:
Total distance:
60+90+120=270 km
Total time:
1+1.5+2=4.5 hours
Average speed:
270/4.5= 60 km/h
Example 6: Average of Grouped Data
Problem: Find the average of the following set of data: 2, 4, 4, 4, 5, 5, 7, 9.
Solution:
Sum of values:
2+4+4+4+5+5+7+9=40
Number of values:
8
Average:
40/8 =5
Average Chapter in Maths PDF
For an average chapter PDF in math, I recommend looking into these types of resources:
NCERT Mathematics Textbooks (Class 11 and 12): These are freely available on the NCERT website and provide detailed explanations, examples, and exercises on average concepts and related topics.
Basic Statistics and Data Handling PDFs: Many education websites provide free PDF resources that cover averages, means, medians, and modes. Websites like Khan Academy and BYJU’S often have such resources.
Mathematics Guidebooks: Books like RS Aggarwal and RD Sharma also offer in-depth explanations on averages and other related concepts. You can often find these as PDFs online or as free previews.
| Related Posts | |
| a³ + b³ and a³ – b³ Formula | Mensuration Formula |
| Algebra Formulas | Profit and Loss Formula |
| Time and Work Formula | Discount Formula |









 Greater Than and Less Than, Equal to Sig...
Greater Than and Less Than, Equal to Sig...
 XXV Number- XXV Roman Numerals Definitio...
XXV Number- XXV Roman Numerals Definitio...
 Ordinal Numbers: Meaning, Examples, Appl...
Ordinal Numbers: Meaning, Examples, Appl...









