In calculus, differentiation is one of the two key concepts along with integration. Differentiation is a technique used to calculate the rate of change of a function. The process of differentiation in Mathematics involves determining the immediate rate of change of a function with respect to one of its variables. Velocity is the most frequent instance of the change in displacement rate over time. Anti-differentiation is the contrary process of finding a derivative.
Differentiation Formulas
Candidates can check some of the most commonly used differentiation formulas below.
- If f(x) = tan (x), then f'(x) = sec2x
- If f(x) = cos (x), then f'(x) = -sin x
- If f(x) = sin (x), then f'(x) = cos x
- If f(x) = ln(x), then f'(x) = 1/x
- If f(x) = ex, then f'(x) = ex
- If f(x) = xn, where n is any fraction or integer, then f'(x) = nxn-1
- If f(x) = k, where k is a constant, then f'(x) = 0
Differentiation Definition
Differentiation is the process of determining a function’s derivative, or rate of change. In contrast to the abstract character of the theory that underpins it, differentiation can be accomplished using only algebraic manipulations, requiring only three basic derivatives, four rules of operation, and a working grasp of functions.
The three basic differentiation are:
(1) Algebraic functions –
| D(xn) = nxn − 1 |
where n is any real number
(2) Trigonometric functions –
| D(sin x) = cos x |
| D(cos x) = −sin x |
(3) Exponential functions –
| D(ex) = ex |
The theory offers the following basic rules for differentiating the sum, product, or quotient of the any two functions f(x) and g(x) whose derivatives are known (where a and b are constants) for functions built up of combinations of these types of functions:
Differentiation Sum Rule
| D(af + bg) = aDf + bDg |
Differentiation Product Rule
| D(fg) = fDg + gDf |
Differentiation Quotient Rule
| D(f/g) = (gDf − fDg)/g2 |
Differentiation Chain Rule
The chain rule is another basic rule that can be used to differentiate a composite function. If f(x) and g(x) are two functions, the composite function f(g(x)) is determined by first evaluating g(x) and then evaluating the function f at this g(x) value. The chain rule asserts that a product gives the derivative of a composite function:
| D(f(g(x))) = Df(g(x)) ∙ Dg(x) |
In other words, the first element on the right, Df(g(x)), indicates that the derivative of Df(x) is determined first as usual, and then x is replaced by the function g wherever it occurs (x).
Differentiation Formula
Differentiation is a fundamental concept in calculus that involves finding the derivative of a function with respect to its independent variable. Here are some differentiation formulas for common types of functions:
Differentiation Formula for Power Rule
If f(x) = x^n, where n is a constant, then the derivative f'(x) is given by:
f'(x) = n * x^(n-1)
Differentiation Formula for Constant Rule
If f(x) = c, where c is a constant, then the derivative f'(x) is:
f'(x) = 0
Differentiation Formula for Sum/Difference Rule
If f(x) = g(x) + h(x), then the derivative f'(x) is the sum of the derivatives of g(x) and h(x):
f'(x) = g'(x) + h'(x)
Differentiation Formula for Product Rule
If f(x) = g(x) * h(x), then the derivative f'(x) is given by:
f'(x) = g'(x) * h(x) + g(x) * h'(x)
Differentiation Formula for Quotient Rule
If f(x) = g(x) / h(x), then the derivative f'(x) is given by:
f'(x) = (g'(x) * h(x) – g(x) * h'(x)) / (h(x))^2
Differentiation Formula for Chain Rule
If y = f(g(x)), where y is a composite function of two functions f and g, then the derivative dy/dx is given by:
dy/dx = f'(g(x)) * g'(x)
Differentiation Formula for Exponential and Logarithmic Functions
- The derivative of e^x is e^x.
- The derivative of ln(x) is 1/x.
Differentiation Formula for Trigonometric Functions
- The derivative of sin(x) is cos(x).
- The derivative of cos(x) is -sin(x).
- The derivative of tan(x) is sec^2(x).
These are some of the basic differentiation formulas. There are additional rules and techniques for more complex functions. Remember that the rules of differentiation allow you to find the rate of change or slope of a function at any given point.
Differentiation Formula of sec x, tan x, cot x, Log x
Some of the most important and basic formulae of differentiation are:
- If f(x) = xn, in which n is any fraction or integer, then
| f'(x) = nxn-1 |
- If f(x) = k, where k is a constant, then
| f'(x) = 0 |
- If f(x) = tan (x), then
| f'(x) = sec2x |
- If f(x) = cos (x), then
| f'(x) = -sin x |
- If f(x) = sin (x), then
| f'(x) = cos x |
- If f(x) = ln(x), then
| f'(x) = 1/x |
- If f(x) = ex, then
| f'(x) = ex |
Differentiation Formulas Chart Class 12
differentiation formulas chart class 12 is given below. Students of class 12 can easily learn all these differentiation formula for their board exams.
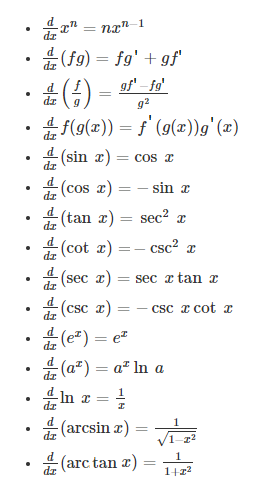
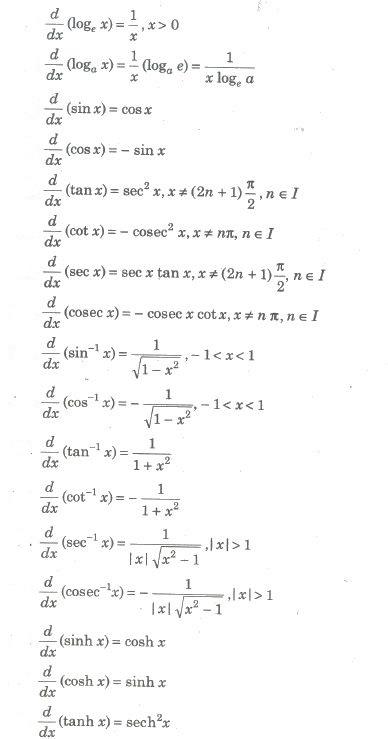
Differentiation Formulas PDF for Class 12
Download the differentiation formula pdf from here.
Differentiation Solved Examples
Q.1: Differentiate f(x) = 6x² – 9x + 4 with respect to x.
Solution:
We have been given: f(x) = 6x² – 9x + 4
On differentiating both the sides w.r.t x, we get;
f'(x) = (2)(6)x – 9
f'(x) = 12x – 9
Hence, the final answer = 12x – 9
Q.2: Differentiate y = x(3x – 9)
Solution:
Given, y = x(3x – 9)
or, y = 3x² – 9x
On differentiating both the sides we get,
dy/dx = 6x – 9
Hence, the final answer = 6x – 9











 Greater Than and Less Than, Equal to Sig...
Greater Than and Less Than, Equal to Sig...
 XXV Number- XXV Roman Numerals Definitio...
XXV Number- XXV Roman Numerals Definitio...
 Ordinal Numbers: Meaning, Examples, Appl...
Ordinal Numbers: Meaning, Examples, Appl...









