Vertical Line- Slope, Equations, Definition, Examples, Image

Table of Contents

Vertical and horizontal alignment are represented in mathematics by vertical and horizontal lines. A vertical line, sometimes known as a standing line, is one that always runs from top to bottom.

Vertical Line

A vertical line is usually a straight line that runs from the top to the bottom or from the bottom to the top. In our daily lives, vertical lines can be in the shape of steel fence rails, long towers, electric poles, tall trees standing upright, table legs, and so on. A vertical line is a perpendicular line to the surface or another line that serves as the base. In this article, we are going learn about the concept of the vertical line and its properties in detail.

What is Verticle Line in Math

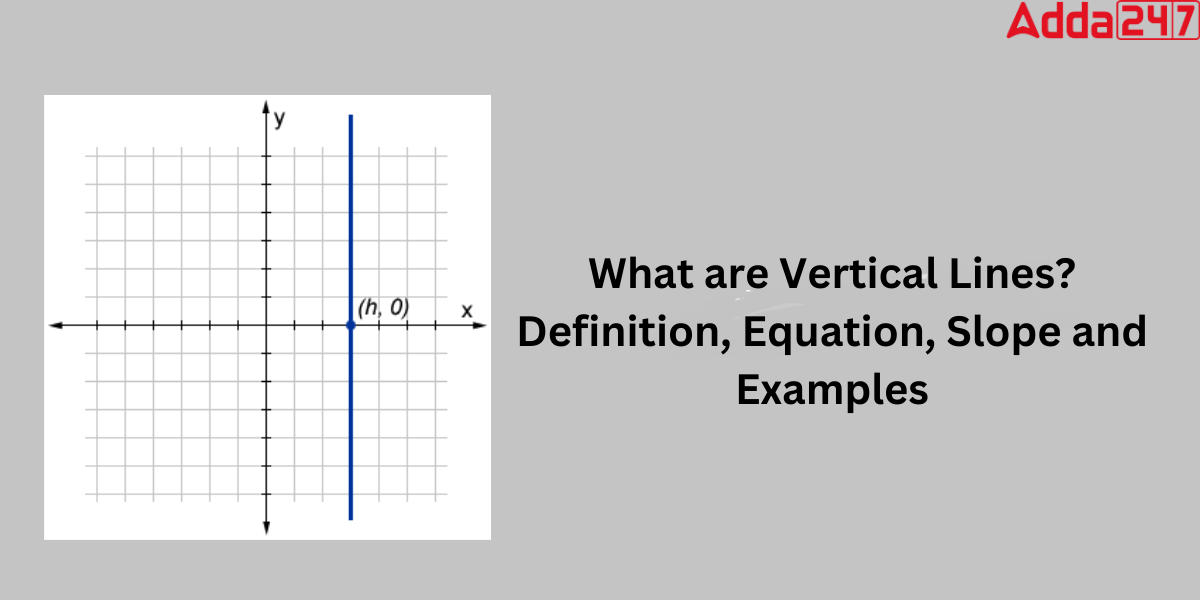
A vertical line is one in which every point has the same x-coordinate that is parallel to the y-axis and perpendicular to the x-axis. In coordinate geometry, the vertical lines are parallel to the y-axis and are perpendicular to the horizontal lines. The y-axis is referred to as the vertical axis on the coordinate plane, and all vertical lines are parallel to it.. Any point in this line will have the same value for the x-coordinate. For example, (2,0), (3,0) (-4,0), etc. are the points of vertical lines.

Vertical Line Equation

Vertical lines are parallel to the y-axis and so have no specified slope. As a result, the equation of the vertical line crossing the x-axis at any point ‘a’ may be found. A vertical line equation is of the form “x = some number”. The x-coordinate of any point on it is referred to as “some number” in this context.

Thus, the equation of a vertical line passing through a point (a, b) is x = a.

where x is the coordinate of a point on the line and ‘a’ is the point at which the lines intersect at the x-intercept.

For Example, For the vertical line equation, x = 13. This line crosses through the x-axis point (11, 0), and several places on this vertical line include (13, -6) and (13, 7), (13, 10), and so on.

Vertical Line on Coordinate Plane

The intersection of the x- and y-axes creates a plane known as the coordinate plane. Vertical lines in the cartesian coordinate system are defined as lines parallel to the y-axis or perpendicular to the x-axis. So, the vertical line is any line that is perpendicular to the y-axis. The y-coordinate of a vertical line is variable whereas the x-coordinate is fixed.We may determine the quadrant in which the points are located using the coordinates that cross through a vertical line.
If the coordinates are represented as (a,b), the x value remains constant regardless of the value of y. For all y values, the vertical line passes through the point ‘a’ on the x-axis. The point (a,0) is the x-intercept of a vertical line x=a.

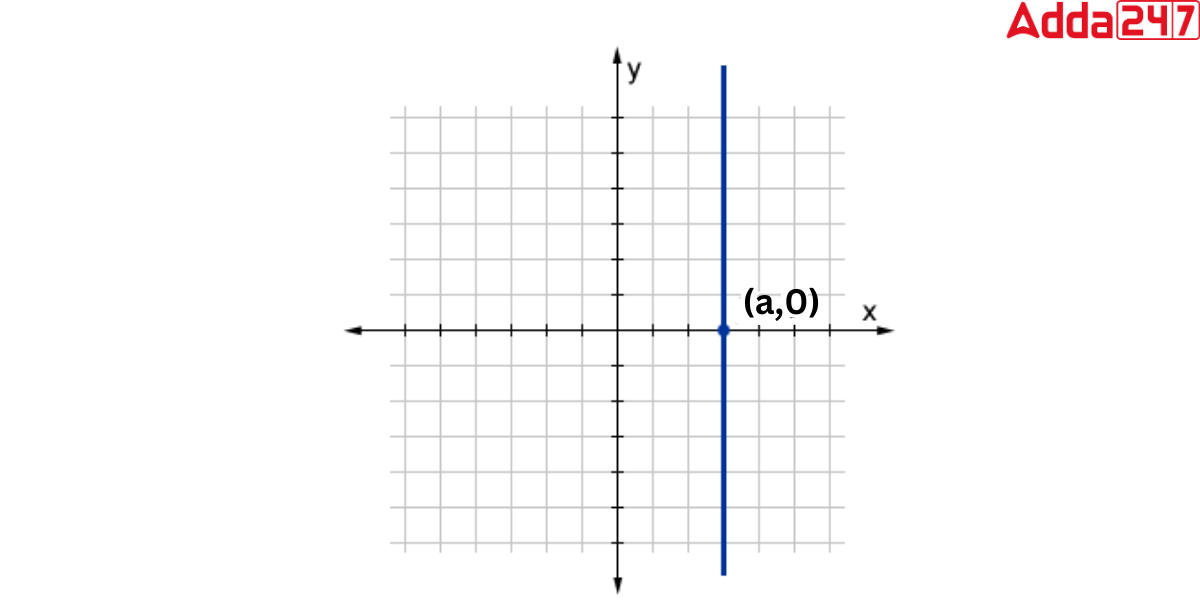
Vertical Line Symbol

From the definition of the vertical Line we came to know that A vertical line is one that is perpendicular to the base of any geometrical object, or, in other words, one that is perpendicular to the horizontal line. As a vertical line is always perpendicular to a surface or another line that is considered a base and is denoted by the symbol ‘|’

Vertical Line Image

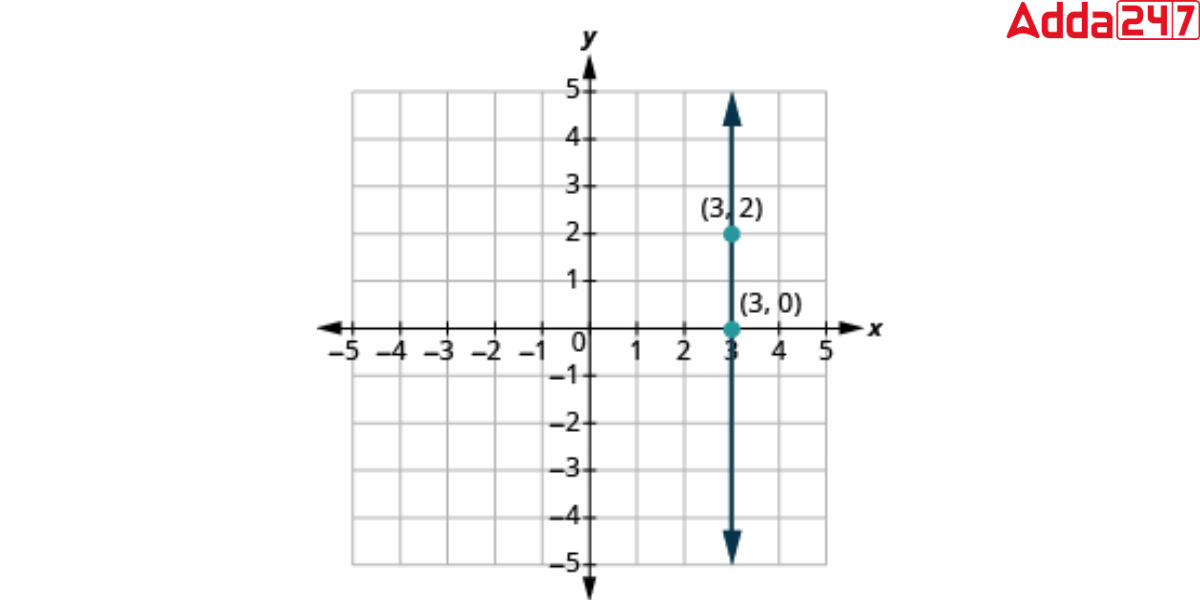
In real life, we observe vertical lines in a variety of situations. A vertical line is used to measure the height of a building a tree or a mountain. In coordinate geometry, x = 3 is a vertical line that passes through the points (3, 0), (3, 2), (3, 4), (3, 10), and so on. This line parallels the y-axis and cuts the x-axis at (3, 0).

The Slope of the Vertical Line is

Since a vertical line forms a 90° angle with the x-axis, its slope is undefined. In accordance with the concept of slope, we determine the slope as follows:

We know that, Slope of a line = Change in y-coordinate/ Change in x-coordinate

OR
m = (y2 – y1) / (x2 – x1)

Since we know that the x-coordinate of a vertical line never changes, x2 = x1 = x and x2 – x1 = 0.

⇒ m = (y2 – y1)/0 = Undefined

As a result, the slope of the vertical line is undefined.

Properties of Vertical Lines

Check out the key properties of a vertical Line listed below:

The equation of a vertical line is always stated as x = a, where a signifies the x-intercept.
Since the line is parallel to the y-axis, a vertical line on the coordinate plane (excluding the y-axis) lacks a y-intercept.
The slope of the vertical line is unknown. Because the x-coordinates do not change, the slope’s denominator is zero.
The vertical line is used in mathematics to determine whether a relation is a function.
Vertical line equations are always of the form x = a, where an is the x-intercept

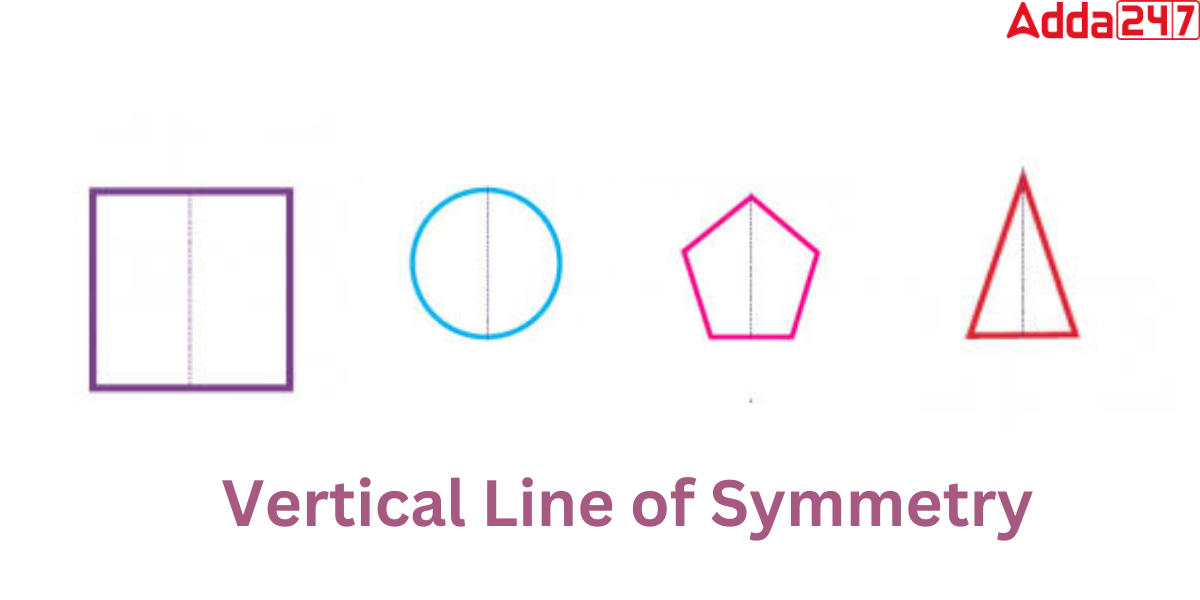
Vertical Line of Symmetry

A vertical line of symmetry is a straight line that runs from the top to the bottom of any figure or object, dividing it into two identical halves that are mirror images of one another. The vertical line of symmetry can be seen in a variety of shapes, such as a square, rectangle, trapezium or circle.The illustration below depicts the vertical symmetry line of certain figures.

Vertical Line Test

From the propertites of vertical Line we came to know that the vertical line is used in mathematics to determine whether a relation is a function. The vertical line test determines whether or not a given graph is a function. A relation is said to be a function only if any vertical line drawn along its graph contacts the graph only once. A function can only have one output for each input.If a vertical line intersects the graph at more than one point, it is read as a function with more than one output, indicating that it is not a function.

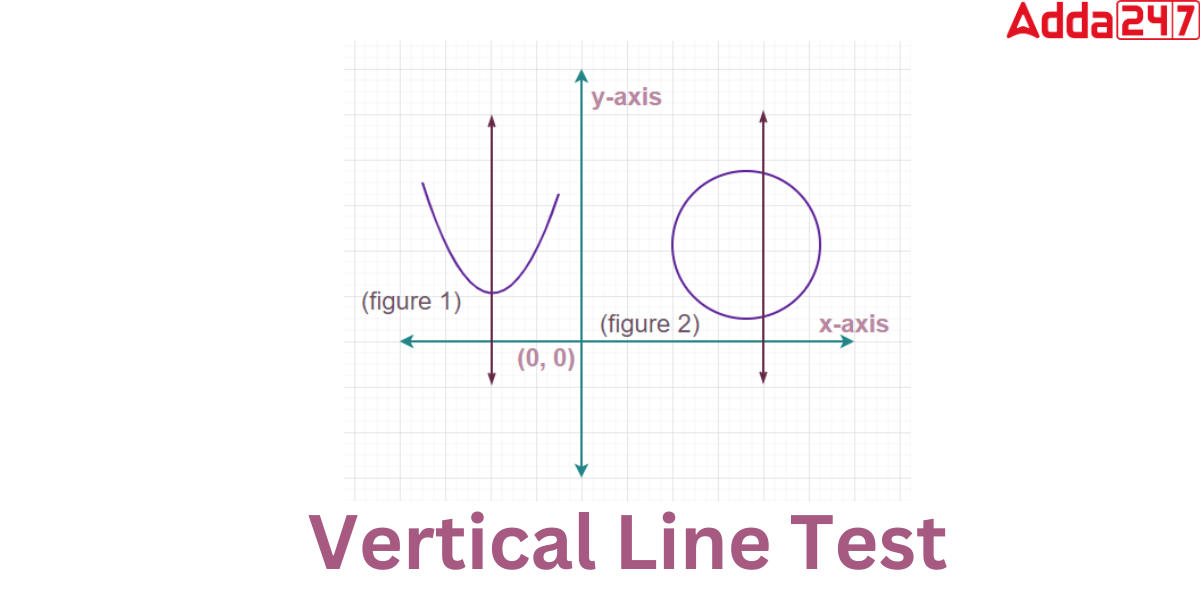
In the above Image, A vertical line drawn to y = f(x) (figure 1) cuts the graph at only one place, indicating that y = f(x) is a function because it passes the vertical line test. But, the graph of y = f(x) (figure 2) is not a function since a vertical line drawn through it cuts it at two points, indicating that it fails the vertical line test.