Straight Angle- Definition, Diagram, Properties, Examples

Straight Angle is one of the most common types of angles found in the real world. You all must have noticed or constructed these angles in your life either knowingly or unknowingly. The line that you construct regularly is a prime example of this angle. It is one of the six types of angles found in geometry. The other five angles are acute angle, right angle, obtuse angle, reflex angle, and complete/full rotation angle. This article will cover all the important aspects of this special so that you do not miss any important points for your exam.

Straight Angle

As it is evident from its name, the straight angle appears straight in appearance. That is, these angles do not form any conical shape. The value of these angles is always equal to 180°. When two rays are linked end to end, they create an angle according to the definition of angles in mathematics. As a result, the two rays with 180-degree angles are subtended in the opposite direction where the rays are connected at ends. The straight angle (180°) is expressed as pi (Π) in radians. This angle register its presence in many real-life scenarios. Let us explore some interesting features of this angle. Before that have a look at its definition and its shape (diagram).

Straight Angle Definition

As per the formal mathematical language, straight angle is an angle whose measure is exactly 180°. In other words, the arms of the rays forming this angle lies in opposite directions. It is the angle that two rays travelling in opposite directions subtends at their common end point. It looks exactly like a straight line, hence the name. It is an angle whose arms unite to make a 180° angle by pointing in opposing directions from the vertex.  The rays forming this angle are travelling in opposite directions, giving a straight line shape to it. The 180° angle is also known as supplementary. The vertex of this angle is flat, hence it is also known by the name of flat angles.

Straight Angle Diagram

The diagrammatic view of the this angle will precise help you understand the reason behind its naming. Its vertex point is completely flat, giving it a straight shape. The diagram of the straight line is shown below.

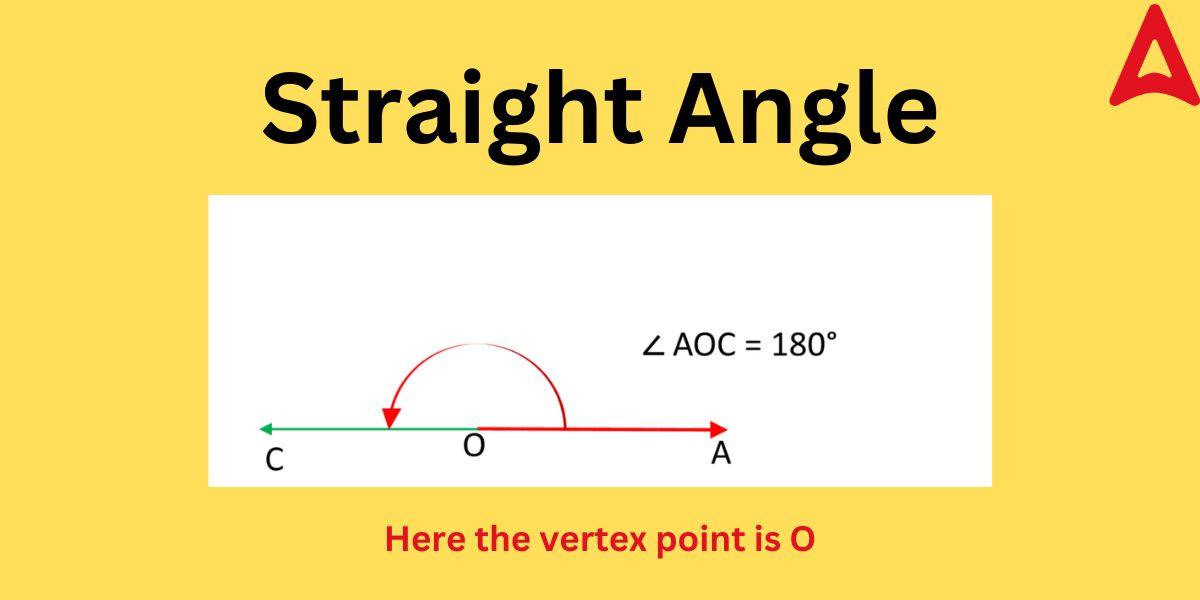
As shown in the above figure, ∠AOC is 180°

OC and AO are two rays travelling in opposite directions that meet at O

This leads to the formation of an angle that is flat or straight with vertex point O.

Straight Angle Degree

The degree of this angle always remain constant. It does not take several values like obtuse angles or reflex angles. The value of its degree always remain 180°. In other words, we can say that the value of this angle lies between an obtuse angle and a reflex angle. The value of an obtuse angle is more than 90° but less than 180° while the value of reflex angle is greater than 180° but less than 360°. We can also conclude from its degree that it is equal to the half rotation, as a full rotation corresponds to 360°. The value of its degree is twice the right angle degree (90°).

Straight Angle Pair

A straight angle pair is a pair of angles that together forms a straight line. The sum total of any such angle pairs is always exactly equal to 180 degrees. In other words, we can say that a these angle pairs always forms a supplementary angle. They are also commonly known by the term “a pair of linear angles”. Let us understand this concept through a diagram.

In the above figure, ∠SOT and ∠UOS forms a this angle pair

where, ∠SOT = 80° and ∠UOS = 100°

These both angles form a supplementary pair that is equal to 180°

These pairs have a common vertex and a common arm.

Here in this figure, OS is the common arm and O is the common vertex.

Straight Angle Formula

As we know that the value of this angle is 180°. So, if the value of one of the angles forming a straight angle pair is known, we can easily deduce the other value by using the following formula:

X = 180° – a

where, X is the unknown angle

a is the value of the known angle

Straight Angle Properties

This special angle shows some unique properties that is not found in any other an and angles. It is because of its special shape and flat vertex point. These properties will help students in recognizing it and its related shapes quite easily. Some of its properties are stated below.

• The value of their degree is always 180
• It is equal to pi (Π) in radians
• The arms of a this angle point in opposite directions
• The vertex point of a this angle is flat
• It is half the full revolution
• It can be obtained by joining two right angles
• The angle can be obtained by rotating a ray by 180° with respect to the other ray.

Straight Angle Examples in Real Life

Many examples of a this special angle can be found in our day to day lives. Some of its examples encountered in real life are listed hereunder.

• The angle formed by the hour hand and the minute hand at 6 O’clock
• The angle formed between the two sides of a book when it is open flat
• The angle between the two arms of a balanced seesaw
• The angle between the closed doors of a wardrobe
• The angle formed by the two fully-extended airplane wings

Straight Angle Solved Examples

Some of the solved examples on this topic is given below for students. These solved questions will help students in cementing a solid foundation in this topic.

Example 1: The value of linear pair of angles are 36°+X and 39°+2X. Solve for the value of X.

Solution: As we know the sum of linear pair of angles is equal to 180°

So, 36°+X+39°+X =180°

=> 75°+3X = 180°

=> 3X = 180°-75°

=> 3X = 105°

=> X = 105°/3

Hence, X = 35°

Example 2: If the measure of one of the angles of an angle pair forming a straight line is 40°, what will be the value of the other angle?

Solution: As we know the straight angle pair forms a straight line, i.e., their sum is 180°.

Let the other angle be Z

So, 40° +  Z = 180°

Z = 180° – 40°

Z = 140°

Hence, the value of other angle will be 140°.

Example 3: Angles Z, Z+10°, and Z+20° form a linear pair. What will be the value of Z?

Solution: As we know the sum of linear pair of angles = 180°

So, Z+Z+10°+Z+20° = 180°

3Z + 30° = 180°

3Z = 180° – 30°

3Z = 150°

Z = 150°/3

Z = 50°

Sharing is caring!