Can we find the sum of an infinite GP whose r is greater than 1?

No, we cannot find the sum of a GP whose common difference (r) is greater than 1.

What will be the sum of GP formula for a GP with the first term a, common difference r and the number of terms as n.

The sum of GP formula for a GP with the first term a, common difference r and the number of terms as n is given by: Sn = a(r^n - 1) / (r - 1) [OR] Sn = a(1 - r^n) / (1 - r)

What will be the sum of a finite GP whose r = 1?

The sum of a finite GP whose r=1 is given by: S = an, where a is the first term and n is the number of terms in a GP

GP Formula- Sum of n Terms, Sum of Infinite GP -

Table of Contents

GP Formula

The general term (or nth term) of a geometric progression (GP) can be given by the formula:

a_n = a \cdot r^{(n-1)}

$a_{n} = a \cdot r^{(n - 1)}$

where:

$a_n$
$a$
$r$
$n$

Additionally, the sum of the first

n

$n$ terms of a geometric progression can be found using:

S_n = a \left( \frac{1-r^n}{1-r} \right) \quad \text{if} \quad r \ne 1

$S_{n} = a (1 - r 1 - r ^{n}) if r \neq = 1$

r = 1

$r = 1$ , the sum is simply:

S_n = n \cdot a

$S_{n} = n \cdot a$

Sum of GP

The formula for the sum of GP is used to calculate the value one would get by summing up all the values occurring in the GP. It is an important concept of Mathematics and statistics that plays an important role in solving different problems in the real world. Thu sum of GP can be asked to calculate whether for the finite series or the infinite series. The formulas for both cases vary as the infinite series sum formula has to take into account an infinite number of terms. In this article, we will learn about the formulas for the sum of GP in different cases.

GP Sum Formula

The GP Sum Formula is used to calculate the sum of all the terms occurring in the Geometric Progression. The GP sum in the finite cases is computed by the below mentioned formulas.

Sum of n terms of GP, S_n = a(1 – rⁿ)/(1 – r), when r ≠ 1
Sum of infinite terms of GP, S_n = a/(1 – r), when |r| < 1

In the above formulas, a is the first term of the GP, r is the common ratio of the GP and n is the number of terms up to which the sum is to be found. Before delving into the details of the sum formula, let us first understand what exactly is a GP.

What is Geometric Progression

Geometric progression is the series or sequence of terms in which the each succeeding term is obtained multiplying or dividing the preceding term by a certain number. That certain number is known as the common ratio. The common ratio is same for all the terms in a GP. The common ratio us denoted by r. If the value of common ratio is more than 1, then the series will have increasing values if we go further and vice versa. Foe example 3, 6, 12, 24, 48, 96 is a GP where the common ratio is 2.

The GP can be either finite or infinite. In a finite GP, there are finite number of terms while in an infinite GP, the number of the terms are infinite. The examples of finite and infinite GP is given below.

Finite GP: 2, 4, 8, 16, 32, 64, 128

Infinite GP: 1/2, 1/4, 1/8, 1/16, 1/32, 1/64, 1/128, 1/256,………………………….

GP Sum Meaning

The total GP sum is the sum total of all the terms appearing in the GP series. A geometric progression’s GP sum is the total of some or all of its terms. Let’s use an example to begin comprehending GP sum. Rani follows a specific routine to save a few rupees each week. Her deposit in week one was Rs 2. Rs 4 in week two, Rs 8 in week three, Rs 16 in week four, and so forth. How much money in her piggy bank will she have at the end of seven weeks? The deposits over the course of seven weeks would total Rs2, Rs4, Rs8, Rs16, Rs32, Rs 64, and Rs128. She will therefore have Rs2 + Rs4 + Rs8 + Rs16 + Rs32 + Rs 64 + Rs128 = Rs254 accrued in her piggy bank at the end of the seven-week period.

Sum of GP Formula

The sum of GP for certain number of terms or all its terms can have different formulas in different scenarios. If the series is finite, then the GP sum formula will be different than the one which is infinite. The sum of GP formula also depends on the common difference r. The sum of GP formula is different when the value of r is greater than 1, equal to 1 or less than 1. These formulas are stated hereunder.

To find the sum of finite (n) terms of a GP,
S_n = a(rⁿ – 1) / (r – 1) [OR] S_n = a(1 – rⁿ) / (1 – r), if r ≠ 1.
S_n = an, if r = 1.

To find the sum of infinite terms of a GP,
S = a / (1 – r), if |r| < 1 (and in this case, we say that the series converges)
S cannot be found if |r| ≥ 1 (and in this case, we say that the series diverges)

where, a = first term of the GP, r = common difference

The formulas have been illustrated in the diagram given hereunder.

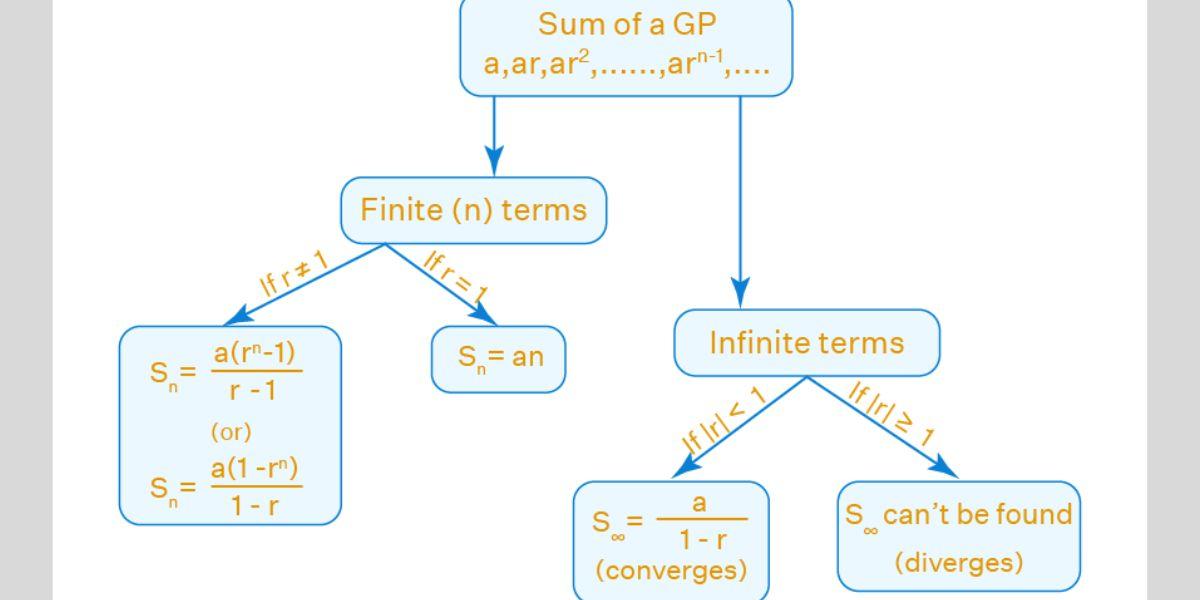
GP Formula Sum of n Terms

We can calculate the sum of n terms appearing in a GP. These n terms can either be in a finite GP or infinite GP. Here n represents the finite number of terms. Let us understand this sum formula by taking an arbitrary example.

Suppose there be a GP with the first term as a and the common difference r. The first n terms of the GP will be then represented by a, ar¹, ar², ar³…………ar^n-1

Let the sum of the geometric series be represented by S

Then S = a + ar + ar²+ … + ar^n-1 … (1)

Multiplying both sided by r, we get

Sr = ar + ar² + ar³ + …… + arⁿ … (2)

on subtracting equation (1) from equation (2), we get

Sr – S = (ar + ar²+ … + arⁿ) – (a + ar + ar²+ … + ar^n-1)

S (r – 1) = arⁿ – a

S (r – 1) = a(rⁿ – 1)

Or, S = a(rⁿ – 1) / (r – 1), which is the desired result

It is important to note here that r is not equal to 1 here.

The formula can be also written as

S = -a(1 – rⁿ) / (-(1 – r)) = a(1 – rⁿ) / (1 – r)

If the value of r becomes 1, then

S = an

Sum of Infinite GP

The sum of infinite terms of a GP is given by

S = a/(1-r)

where a = first term of the infinite GP

r = common difference

We can find out the proof for the sum of infinite terms of GP formula by using simple mathematical calculations. The proof for the same is given below.

Let the infinite GP series be a, ar, ar², ar³,………

S = a + ar + ar² + ar³ + …………………. (i)

where, S = sum of the series

multiplying equation (i) by r on both sides

rS = ar + ar² + ar³ + ar⁴+……………………………. (ii)

subtracting the equation (ii) from equation (i), we get:

S – rS = (a + ar + ar² + ar³ + ………………….) – (ar + ar² + ar³ + ar⁴+…………………………….)

S (1-r) = a

or, S = a/(1-r)

The infinite GP sum can only be calculated when the value of r is less than 1. When the r becomes greater than 1, then the values of GP becomes more larger. For example the series: 2, 4, 8, 16, 32, 64, 128, 256, …….. is an infinite GP with common ratio of 2. As we can observe from the above-given infinite series, the values of each successive terms gets bigger and bigger. In this case, after a certain point in the series, the terms of the series expand quickly and take on very large values. Consequently, the series diverges, failing to converge to a finite value, and the sum of a GP with r > 1 cannot be obtained. So we can say that, the sum of infinite terms of a GP formula does not exist when r > 1.

GP Sum Formula – Important Notes

The important notes an takeaway from the GP sum formula is given below.

The sum of GP (of n terms) is: S_n = a(rⁿ – 1) / (r – 1) [OR] S_n = a(1 – rⁿ) / (1 – r), if r ≠ 1.
The sum of GP (of n terms) is: S_n = na, when r = 1.
The sum of GP (of infinite terms) is: S_∞ = a/(1-r), when |r| < 1.
The sum of GP (of infinite terms) is: S_∞ = does not exist, when |r| ≥ 1.

GP Sum Formula – Solved Examples

Some of the solved examples the sum of GP formula is given below. By going through these questions, students will have a better understanding on how to use the sum of GP formula in solving numerical problems.

Example 1: What will be the sum of a GP whose first term is 6 and the common ratio is 1/2. Given that the number of terms in the GP is 10.

Solution: As the GP is finite and given,

First term (a) = 6

common ration (r) = 1/2

n = 10

as r < 1

so we will use the formula for GP sum which is given by

S = a(1 – rⁿ) / (1 – r)

On substituting the values, we get

S = 6 (1 – (1/2)^10)/(1-1/2)

S= 6(1-1/1024)/(1/2)

S = 6 (1023/1024)/(1/2)