Rate of Change Formula in Maths

Table of Contents

The rate of change formula describes the link between how one quantity/ number/ value changes with respect to how another quantity changes. In a nutshell, the rate of change (ROC) is the pace at which a variable changes over time. The slope of a line illustrates the rate of change graphically. The Greek letter delta (Δ) is frequently used to represent the ROC. In this post, we are going to discover the formula of rate of change, rate of change based problems, its applications, and much more.

Rate of Change Formula

Basically, the rate of change formula divides the amount of change in one item by the equivalent quantity of change in another.

In accordance with the context, the rate of change may be referred to by different phrases. Acceleration/deceleration, for example, is the rate of change with respect to speed or velocity.
The slope of the line of best fit defines the pace of change in statistics and regression modeling. It is the population growth rate. Momentum is a term used in financial markets to describe the rate of change.
The rate of change from y coordinates to x coordinates can be calculated as Δy/ Δx = (y2 – y1 )/ (x2 – x1).
The rate of change m for a linear function has been provided in the slope-intercept form for a line: y=mx+b, but the rate of change of variables is otherwise stated to be (f(b)-f(a))/ b-a.

What is the Rate of Change (ROC)?

The moving average of a variable can be measured by the rate of change, which is used to mathematically express a percentage change in value over a specific period of time. In finance, ROC (Rate of Change) can be calculated as a return over time by taking the present value of a stock or index and dividing it by the value from a previous period. To convert it to a percentage, subtract one and multiply the result by 100.

In general, the rate of change formula is:

R = \frac{(D_{2 -} D_{1)}}{T}

where, R is the rate of change.
D = the distance (or other variable) calculated at the start and end of the time
T is the amount of time it needed for that shift to occur.

Formula of Rate of Change in Algebra

The incorporation of derivatives in estimating the rate of change of variables with regard to other quantities is an immensely significant function. Let’s start with the three most important aspects of the formula of rate of change, which are listed below.

Formula 1: The fundamental rate of change formula is:
rate of change = (Change in amount 1) / (Change in quantity 2)
Formula 2: If a quantity ‘y’ changes in response to a change in another variable ‘x’, and an equation of the form y = f(x) is always met, implying that ‘y’ is a function of ‘x’, then the rate of change of ‘y’ with regard to ‘x’ is given by

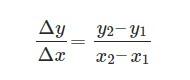
Formula 3: Function rate of change –

(f(b)-f(a))/b-a

Examples of Rate of Change Formulas

Question: Determine the rate of change for the following data using the rate of change formulas.
A cyclist went 40 kilometers in four hours and 180 kilometers in six hours. Calculate the rate of change now.

Solution:
To determine the rate of change in the travel of the cyclist for different hours.
Using the rate of change equation,
(Change in amount 1) / (Change in quantity 2) = rate of change
Rate of change = (distance change) / (time change)
Rate of change = (180-40) / (6-4)
change rate = (140) / (2)
Rate of change = 70

What is the Average Rate of Change Formula?

The Average Rate of Change is characterized as the average rate at which one value/quantity changes in relation to another quantity changing. In simplest terms, an average rate of change function is an approach that divides the amount of change in one object by the amount of change in a different one.

This expression below gives the average rate of change of a function (f) throughout the interval a ≤ x ≤ b.

\frac{(f) a - (f) b}{b - a}

It quantifies how much the function altered per unit on average over that time interval. The slope of the straight line joining the interval’s ends on the function’s graph is used to calculate it.

Rate of Change Formula Practice Problems

Question 1: Determine the average rate of change of f(x) = x2 – 9x in the range 2 ≤ x ≤ 7.
Solution:
f(x) = x2 – 9x
a = 2, b = 7
f(a) = f(2) = (2)2 – 9(2) = 4 – 18 = -14
f(b) = f(7) = (7)2 – 9(7) = 49 – 63 = -14
The average rate of change is as follows:

= \frac{- 14 - (- 14)}{7 - 2} = \frac{- 14 + 14}{5} = 0

As a result, f(x) = 0.

Uses of Rate of Change Formula

The rate of change indicates how something evolves over time. There are many applications of formula of rate of change in our daily lives some of are are mentioned below.

It is also regarded as a major financial idea. It enables investors to identify security dynamics as well as additional developments.
Traveled distance by a car in a given amount of time can be derived from the rate of change.
Each of the volts of higher voltage causes the current flowing through an electrical circuit to rise by a certain number of amps.
The rate of change is also a powerful indicator of market bubbles. Even if momentum is strong and traders seek assets with a positive ROC, a substantial rise in the ROC of a broad-market exchange-traded funds index, or mutual fund in the short term may indicate that the market is unsustainable.
Work completed per unit of time can also be measured by this formula.
Work completed and the number of employees necessary to complete it is another application of Formula of rate of change.

Rate of Change Formula in Calculus and Maths

The rate of change is a fundamental concept in algebra and calculus that measures how a quantity is changing with respect to another variable. It can be expressed using different formulas depending on the context. Here are some of the common rate of change formulas:

Algebraic Rate of Change (Average Rate of Change): This formula calculates the average rate of change of a function over a given interval.Average Rate of Change (AROC) of a function f(x) from x = a to x = b is given by: $A ROC = f ( b ) - f ( a )/b-a$
Calculus Rate of Change (Instantaneous Rate of Change): In calculus, the instantaneous rate of change at a specific point is represented using the derivative of a function. If you have a function
$f (x)$ , the instantaneous rate of change at

$x = a$ is given by the derivative

$f^{'} (a)$ .

$I n s t an t an eo u s R a t e o f C han g e = f^{'} (a)$
Rate of Change for Linear Functions: For linear functions of the form $f (x) = m x + b$ , where

$m$ is the slope of the line, the rate of change is simply equal to the slope.
Rate of Change in Distance over Time: In physics and real-world applications, rate of change often refers to speed or velocity. If an object’s position is a function of time, $s (t)$ , then the rate of change of distance with respect to time is the velocity, and it can be calculated as:
$V e l oc i t y = d t/ d s$
Rate of Change in Growth/Decay: In exponential growth or decay, the rate of change can be calculated using the derivative. For exponential growth, if you have a function $f (t) = a \cdot e^{k t}$ , the rate of change is given by: $R a t eo f C han g e = df = k \cdot a \cdot e^{k t}$

These are some of the fundamental rate of change used in algebra, calculus, and mathematics in general. The specific formula you use depends on the context and what you’re trying to measure or analyze.