Everyone of you must have calculated the square of any number, also known as the perfect square. A perfect square is a number that is the result of multiplying an integer by itself. Multiplying a whole number by itself results in a Perfect Square, such as 4 being the result of multiplying 2 by itself (2 × 2 = 4), making it a perfect square. In this article, we will learn about the definition and formula of perfect squares along with some of its tips and tricks.
Perfect Squares
When a number is multiplied by itself, the result is referred to as a perfect square and can be written as the second exponent of an integer. Therefore, perfect squares refer to the squares of all whole numbers.
Mathematically speaking, the perfect square can be represented as a², called as a superscript 2. They always have a value of zero or above, and are important for comprehending square roots, quadratic equations, and number theory. A perfect square is a number that is the result of multiplying an integer by itself.
What is a Perfect Square?
A positive integer that is the result of multiplying an integer by itself is called a perfect square. Put simply, perfect squares are numbers that result from multiplying integers by themselves. Typically, we can represent a perfect square as x², where x is a integer and x² is a perfect square.
Perfect Square Definition
A perfect square is an integer that can be written as the square of another integer. In simpler terms, it is the result of multiplying an integer (both positive and negative values) by itself.
For example, 36 is a perfect square as it can be obtained by multiplying 6 by itself. Another example is 4, which is 2 times 2.
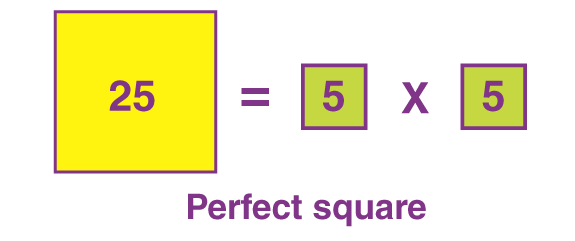
Perfect Squares Formula
Assuming N is a perfect square of a whole number x, we can express this as N = x times x = x². Therefore, the formula for perfect squares can be written as:
N = x²

Perfect Square Numbers
It is a known fact that the square of a number is the result of multiplying that number by itself. Put simply, perfect squares are the result of squaring whole numbers like 1 or 12, 4 or 22, 9 or 32, 16 or 42, 25 or 52, and so forth. You can better understand the building concept of perfect square numbers by looking at the pictorial diagram given below.
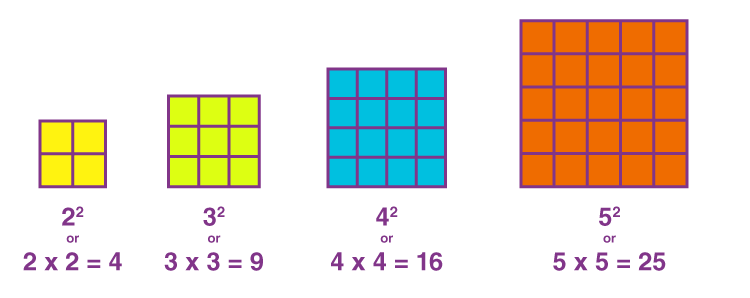
Perfect Squares Examples
Check the examples of perfect square numbers below.
9 = 3 * 3
4 = 2 * 2
25 = 5 * 5
121 = 11 * 11
676 = 26 * 26
576 = 24 * 24
625 = 25 * 25
400 = 20 * 20
Perfect Squares Tips and Tricks
When working with perfect squares, it is essential to remember the following tips and tricks in order to solve questions quickly.
- A square number that finishes with 0 will consistently contain an even amount of zeros at the end.
- Perfect squares are always positive since the product of two negative numbers results in a positive number.
- Perfect squares can have both positive and negative square roots.
- Perfect cubes can be obtained by multiplying a number by itself three times.
- In order to determine if a certain number is a perfect square, we can find the square root of the number. A perfect square is a whole number if its square root is also a whole number. If the square root is a decimal, then the number is not a perfect square.
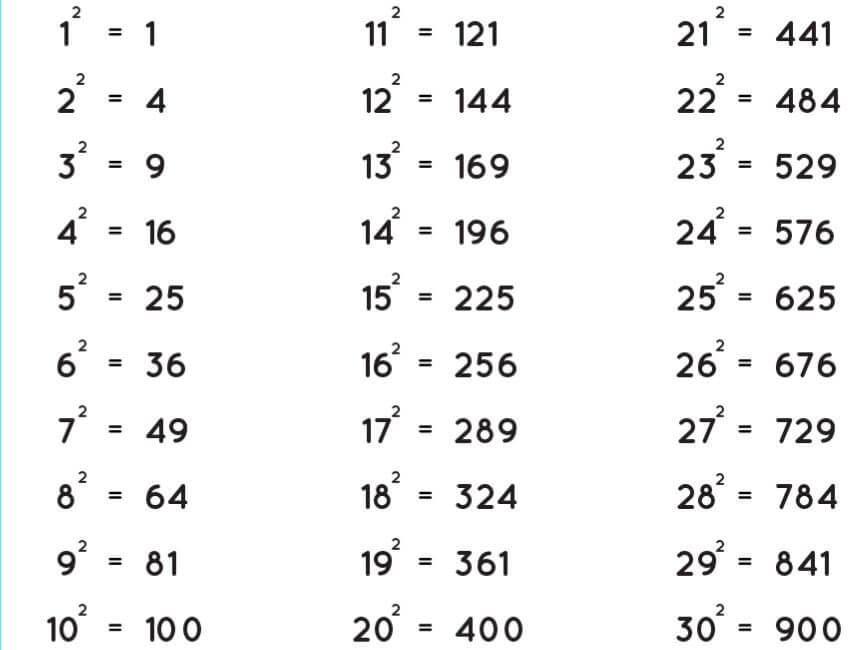
Perfect Squares Chart
The chart on perfect squares for candidates is given below. Candidates can consult this chart whenever they want to know the square of any number.
How to Identify Perfect Square Numbers
Take note of the final digit of the perfect square numbers from 1 to 20 as provided in the table above. You will observe that they finish with one of these numbers: 0, 1, 4, 5, 6, or 9. Upon experimenting with different perfect square numbers, you would have noticed a key characteristic of perfect squares.
Numbers with 2, 3, 7, or 8 in the units place aren’t perfect squares, while those with 0, 1, 4, 5, 6, or 9 might be perfect squares. One can make the following observations to recognize a perfect square number.
- Numbers that end in 3 or 7 will always result in a square number with 9 as the units place digit.
- Any number that ends with 5 will always have 5 as the units digit in its square.
- Numbers that end in 4 or 6 will have 6 as the last digit in their square.
- A number that ends with 2 or 8 will result in having 4 as the last digit in its square.
- Numbers that end in 1 or 9 will always have 1 as the last digit when squared.
Alternate Method to Identify Perfect Squares
One more method to determine if a number is a perfect square is by finding the square root of the number in question. A perfect square is a whole number if its square root is an integer. If the square root is not an integer, then the number is not a perfect square.
For instance, if we want to determine if 24 is a perfect square, we can find its square root. The square root of 24 is 4.89. It is evident that 4.89 is a decimal, thus, 24 is not a perfect square. Let’s look at another instance of the number 81. The square root of 81 is 9. 9 being a whole number implies that 81 is a perfect square.
Perfect Squares List 1 – 10000
Candidates can check the perfect squares list that is found from number 1 to 10,000. The square numbers have been segregated in different groups based on their unit digits. Carefully observe the last digits of the perfect square numbers and their constituting integer.
| Perfect Squares with its Integers |
| 1² = 1 |
| 11² = 121 |
| 21² = 441 |
| 31² = 961 |
| 41² = 1681 |
| 51² = 2601 |
| 61² = 3721 |
| 71² = 5041 |
| 81² = 6561 |
| 91² = 8281 |
| 2² = 4 |
| 12² = 144 |
| 22² = 482 |
| 32² = 1024 |
| 42² = 1764 |
| 52² = 2704 |
| 62² = 3844 |
| 72² = 5184 |
| 82² = 6724 |
| 92² = 8464 |
| 3² = 9 |
| 13² = 169 |
| 23² = 529 |
| 33² = 1089 |
| 43² = 1849 |
| 53² = 2809 |
| 63² = 3969 |
| 73² = 5329 |
| 83² = 6889 |
| 93² = 8649 |
| 4² = 16 |
| 14² = 196 |
| 24² = 576 |
| 34² = 1156 |
| 44² = 1936 |
| 54² = 2916 |
| 64² = 4096 |
| 74² = 5476 |
| 84² = 7056 |
| 94² = 8836 |
| 5² = 25 |
| 15² = 225 |
| 25² = 625 |
| 35² = 1225 |
| 45² = 2025 |
| 55² = 3025 |
| 65² = 4225 |
| 75² = 5625 |
| 85² = 7225 |
| 95² = 9025 |
| 6² = 36 |
| 16² = 256 |
| 26² = 676 |
| 36² = 1296 |
| 46² = 2116 |
| 56² = 3136 |
| 66² = 4356 |
| 76² = 5776 |
| 86² = 7396 |
| 96² = 9216 |
| 7² = 49 |
| 17² = 289 |
| 27² = 729 |
| 37² = 1369 |
| 47² = 2209 |
| 57² = 3249 |
| 67² = 4489 |
| 77² = 5929 |
| 87² = 7569 |
| 97² = 9409 |
| 8² = 64 |
| 18² = 324 |
| 28² = 784 |
| 38² = 1444 |
| 48² = 2304 |
| 58² = 3364 |
| 68² =4624 |
| 78² = 6084 |
| 88² = 7744 |
| 98² = 9604 |
| 9² = 81 |
| 19² = 361 |
| 29² = 841 |
| 39² = 1521 |
| 49² = 2401 |
| 59² =3481 |
| 69² =4761 |
| 79² = 6241 |
| 89² = 7921 |
| 99² = 9801 |
| 10² = 100 |
| 20² = 400 |
| 30² = 900 |
| 40² = 1600 |
| 50² = 2500 |
| 60² =3600 |
| 70² =4900 |
| 80² = 6400 |
| 90² = 8100 |
| 100² = 10000 |










 Greater Than and Less Than, Equal to Sig...
Greater Than and Less Than, Equal to Sig...
 XXV Number- XXV Roman Numerals Definitio...
XXV Number- XXV Roman Numerals Definitio...
 Ordinal Numbers: Meaning, Examples, Appl...
Ordinal Numbers: Meaning, Examples, Appl...









