Length Width Height – Definition, Formula, Solved Examples

We all encounter various geometrical shapes in our day-to-day lives. While passing through these shapes, like skyscrapers, we often talk about their height. We check the length and width of a bat before buying it. All these terms, that is, length, width, and height are nothing but dimensions of a geometrical shape. These dimensions are used to define the magnitude of a geometrical shape. In other words, these are measurements of a geometrical shape. In this article, we will understand these terms in a detailed manner by exploring its various aspects.

Length Width Height

Understanding the ideas of length, width, and height is essential in the fields of mathematics and geometry. When describing the size, form, and orientation of objects in space, these three dimensions are of utmost importance. 3-Dimensional objects possess all three while 2-Dimensional geometrical figures consist only length and width. The width is also known by the name breadth and the height is sometimes called depth. A geometrical shape’s longest side is known as its length, its shortest side its width or breadth, and its vertical dimension is its height or depth. Let us understand their true meaning by understanding their mathematical definition.

Length Width Height Definition

Three measurements are frequently employed to describe an object’s size: length, width, and height. In contrast to width, which is used to measure an object’s width from side to side, length is used to gauge an object’s length from one end to the other. Height is a term used to describe an object’s height from top to bottom. These are the basic measures needed to determine an object’s dimensions. The definition of each of these terms is given below in a detailed manner.

Length: The distance between two end points of an object is measured in length. The length of a figure, which is its longest dimension, indicates how long an object or figure is. Linear units like meters, centimeters, inches, and other measurements are used to express it.

Width: The shorter distance of an object or figure is its width, which indicates how wide or broad the provided figure is. It is also known as breadth, especially in 2D figures like rectangles. Additionally, the width can be measured in linear units such as meters, centimeters, inches, and so forth.

Height: Height is the vertical dimension of an object or geometrical shape. It is sometimes referred to as depth. This dimension is not present in 2D objects and are found only in present in 3D objects. It indicates how high or deep an object is. Linear units like meters, centimeters, inches, and so forth are used to indicate an object’s height or depth.

The terms length, width, height, and depth, respectively, are derivations of the words long, wide, high, and deep. They thereby convey an object’s proportions. These dimensions will be more clear to you by observing the figure of a cuboid given below.

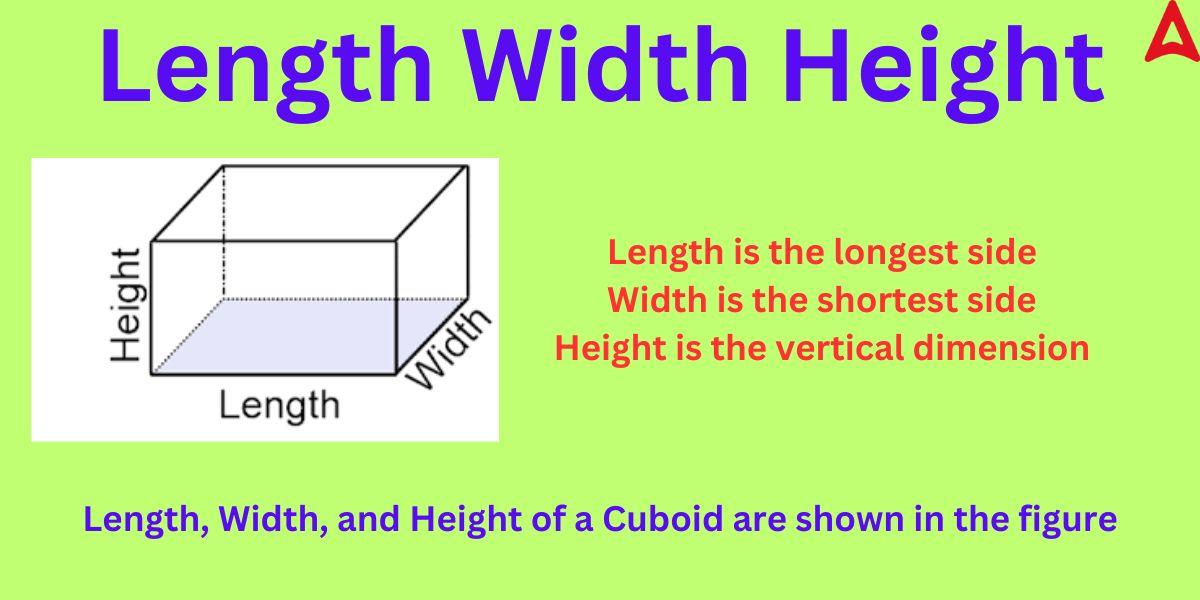
As one can observe from the above figure of a cuboid that length is the longest side while the width is the shortest side. Height or depth is the vertical dimension.

How to Write Dimensions of Length Width Height

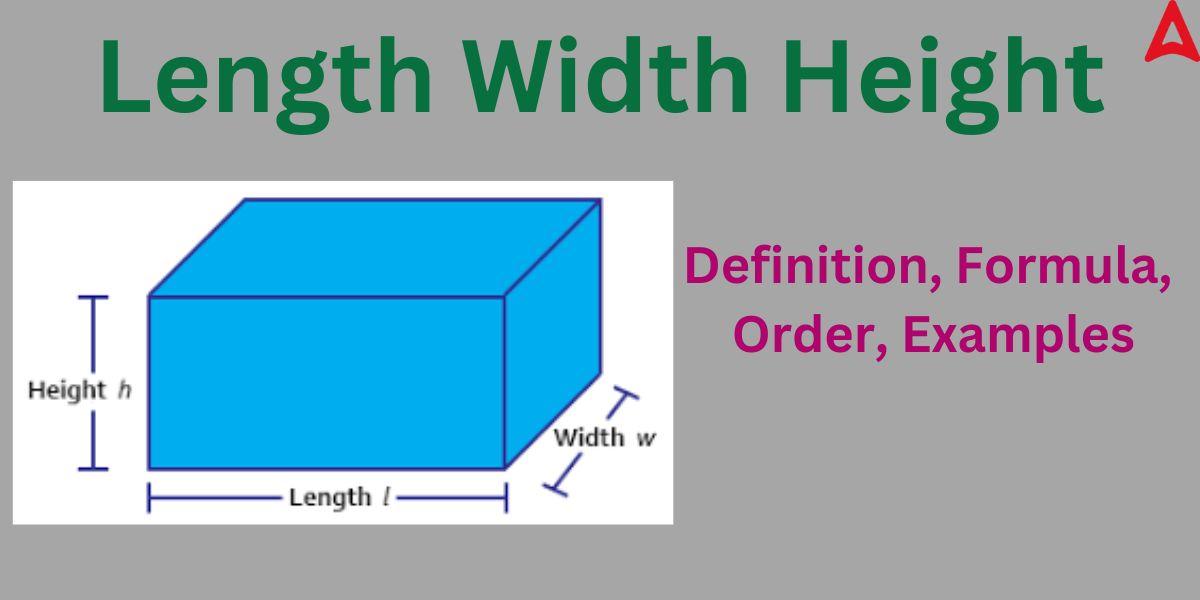
We can write the dimensions of length, width, and height quite easily as we now know their defining properties. If we have been given a 2D geometrical shape, then we know that it can have only two dimensions, a length and a width (breadth). In a typical 3D shape, we will find all three dimensions of length, width, and height. The longest side in the figure will be labelled as the length. The vertical dimension will be written as the height or depth. The remaining side will be called width or breadth. This concept is shown in the above diagram. These dimensions can be expressed in units like meters, centimeters, inches, and so forth.

Length x Width x Height

The three dimensions when multiplied together yield volume of some geometrical shapes. volume is the quantity of space occupied by any geometrical shape. When determining the volume of a geometrical object like a rectangular prism, also known as a cuboid, the length, width, and height are typically utilized in conjunction. The volume of a cuboid is equal to its length, breadth, and height multiplied. In other words, if we multiply all three dimensions together, we may determine the volume or capacity of a cuboid or any rectangular box. Mathematically,

Volume of a rectangular prism or box = Length x Width x Height

For example, if length, width, and height of a rectangular prism is given as 4, 5, and 6 units respectively, then its volume will be given as 4 x 5 x 6 = 120 cube units.

Length vs Width

Both length and width are measures of a side but there is a remarkable difference between these two. Length is the longest dimension while breadth is the shortest dimension. Length is always larger than the breadth. In other words, the distinction between a figure’s length and width is that length denotes a figure’s longer side, while width denotes its shorter side. Width (breadth) shows the wide nature of a geometrical shape while the length depicts how long a shape is. If two measures of a geometrical shape are given to be 10 cm and 7 cm, then we can easily say that 10 cm is the length and 7 cm is the width.

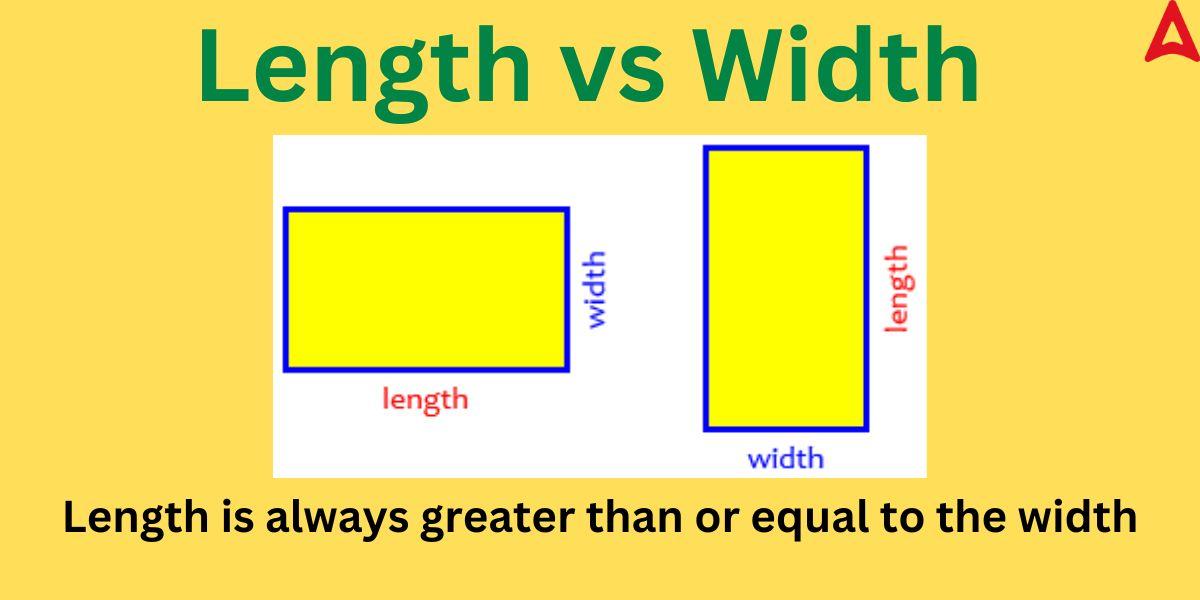
As one can conclude from the above diagram that the length of a geometrical shape is always greater than its breadth.

Length Width Height Order

There is a strong relation between the order of length and width of a particular geometrical shape. But there is no co-relation between height and the other two dimension. Height (sometimes known as depth) is the vertical length of a rectangular 3D shape. Length of a geometrical shape is always bigger than its width. So, we can say the order of magnitude of length is always greater than the order of magnitude of width. The measurements are always written in the order of length, width, and height. That is, if the dimensions of a 3D rectangular shape is given as 20 cm, 11cm, and 15 cm, then 20 cm is the length’s measurement, 11 cm is width, and 15 cm is height of the given shape.

 Length Width Height in Rectangle

As we know that a rectangle is a 2D shape, so, it has only length and width but the rectangular shape in 3D like a rectangular box or a rectangular prism (cuboid) has all three dimensions: length, width, and height. So, we can say that extensions of rectangular shape in 3D contains length, width, and height.

Length Width Height Formula

The length, width, and height dimensions can be used to calculate volume and surface area of a rectangular prism. Length, width and heigh formula for the same is tabulated below.

Volume of a rectangular prism: length x width x height

Lateral Surface Area of a rectangular prism: 2 [(length x width) + (width x height)]

Total Surface Area of a rectangular prism: 2 [(length x width) + (width x height) + (length x height)]

Length Width Height of a Box

We can easily express the length, width, and height of a box by looking at its shape. Because we are aware that a box’s length is its longest side, its width is its short side, and its height is its vertical dimension, we can quickly determine the length, width, and height of a given box. The length, followed by the breadth, the height, and finally the other dimensions, are always expressed in that order. This indicates that if a box’s dimensions are to be measured, they should be stated as length, breadth, and height. For instance, 20 meter, 15 meter, and 18 meter denotes the box’s length (20 meter), its width (15 meter), and its height (18 meter).

Length Width Height Examples

Some of the solved examples on the topic of length, width, and height is given below. These solved problems will help students understand this topic in a better way.

Example 1: The dimensions of a 2D rectangular shape is given to be 10 meter and 15 meter. What will be the dimension of the length?

Solution: As we know, the longer side is always length, so the dimension of the length will be 15 meter.

Example 2: It is given that the dimension of a rectangular box is 16 m, 12 m, and 14 m. What will be the value of the height of this rectangular box?

Solution: Given the dimension in order: 16 m, 12 m, and 14 m

As we know, the dimension of the rectangular shape in 3D is given in the order of length, width, and height.

So, from this comparison, we get height = 14 meter

Example 3: The length, width, and height of a rectangular prism is given as 12m, 10m, and 11 m. Determine its volume.

Solution: Given length = 12m

width = 10m

height = 11m

As Volume = length x width x height

so, volume = 12 x 10 x 11

Hence, volume = 132 m³

Sharing is caring!