Integration of Cot x – Explanation, Formula, Derivation, Examples

Integration of Cot x: Cot x is one of the six fundamental trigonometric ratios apart from Sin x, Cos x, Tan x, Cosec x, and Sec x. The integration of Cot x, also known as the integral of Cot x, is an important concept in the calculus domain of mathematics. Cot x is the opposite ratio of Tan x. Cot x can be defined as the ratio between Cos x and Sin x. In a right-angled triangle having x as one of the acute angles, Cot x is given by the ratio between the side adjacent to x and the side opposite to x. The adjacent side is known as the base while the opposite side is known as perpendicular. That is,

Cot x = Base/Perpendicular = Cos x/Sin x

Integration of Cot x

The integration of Cot x basically gives us the sum or accumulated values of Cot x over a given range. We can find out the integral value of Cot x easily using the method of integration. The integral value of Cot x gives us Sin x. We will understand how this result through a proof. But let us first recall the concept of Integration.

Definition of Integration

Integration is basically summing up the relevant values over an interval. It is one of the fundamental operations in calculus. The calculation of an integral is known as integration. Numerous important quantities in mathematics, such as areas, volumes, displacement, etc., can be found using integrals. Integration is the opposite of Differentiation, the other fundamental operation of calculus. The integration is denoted by the sign ∫. The general formula of integral is given by:

∫xⁿ dx =xⁿ⁺¹/(n+1) + C

The above integration can be said as integration of xⁿ with respect to x.

where x = any variable

Integration of Cot x Formula

Cot x is an integrable function. The integral of Cot x with respect to x is denoted by ∫Cot x dx. Let us observe the formula of the integral of Cot x

The integration of Cot x is given by:

∫Cot x dx = ln | Sin x | + C

where, ln = natural log

C = any constant

It must be noted that Cot x is not defined at values 0, and even multiples of Π. So apart from these values, we can find the integral of all other values of Cot x. So, we can say that Cot x is integrable at all values except at 0 and even multiples of Π.

Integration of Cot x in terms of Cosec x

We can find the integral of Cot x in terms of Cosec x. As we observed in the above formula that the integral of Cot x results in Sin x. We know that Sin and Cosec are strongly related. Cosec x is basically the inverse function of Sin x. That is Cosec x = 1/Sin x. So we can find the integral of Cot x in terms of Cosec x. The same has been shown below.

The integration of Cot x in terms of Cosec x is expressed as:

∫Cot x dx = – ln | Cosec x | + C

As we can observe from the above diagram and formulas, the difference between the integral values of Cot x in terms of Sin x and Cosec x is the negative sign. For ease of calculation purposes, natural logarithm (ln) can be replaced with the common logarithm (log).

Integration of Cot x Proof

The result of the integration of Cot x in terms of Sin x can be proved using simple rules of integration. The same proof has been demonstrated below.

Here, f(x) = Cot x

∫f(x) dx = ∫(Cot x) dx

as Cot x = Cos x/Sin x

so, ∫(Cot x) dx = ∫ (Cos x/Sin x) dx

or, (Cot x) dx = ∫ (1/Sin x). Cos x dx ———-(i)

We will now apply the substitution rule of integration.

Let b = Sin x

Taking derivatives on both sides

So, db = Cos x dx   (because derivative of Sin x = Cos x)

Cos x dx = db

putting this value of Cos x dx in equation (i), we get

∫ Cot x dx = ∫(Cos x /Sin x) dx = ∫ (1/b) db

as, ∫ 1/x dx = ln|x| + C, where ln = natural log and C = constant

so, ∫ Cot x dx = ln |b| + C

putting the value of b = Sin x, we get

= ln |Sin x| + C

Hence proved

If we want to further prove it in terms of Cosec x, then we can proceed as

Sin x = 1/Cosec x

so, ln |1/Cosec x| + C

or, ln | (Cosec x^-1 )

as  log(y)^x = x log(y)

so,  – ln |(Cosec x)| + C

Therefore, ∫ Cot x dx = -ln |Cosec x| + C = ln| Sin x| + C

Integration of Cot x Graph

The integral values of Cot x can be shown graphically. The same has been illustrated in the following diagram.

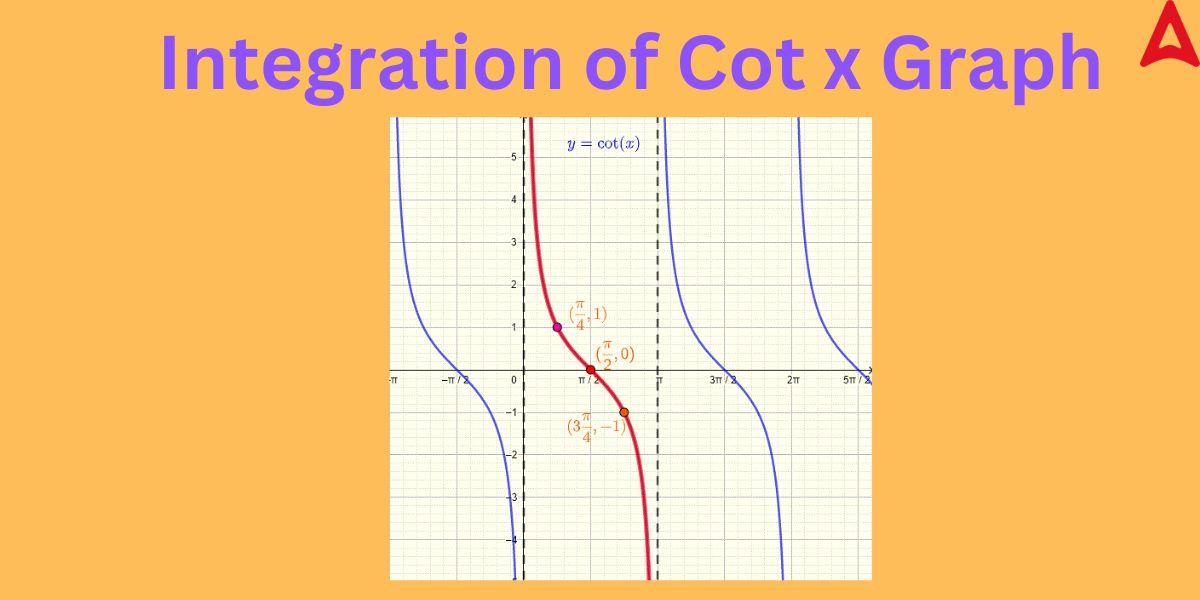
As we can see from the above graph that the domain of Cot x is undefined for 0 and even multiples of pi. So we can conclude that the integration of Cot x is undefined for 0 and even multiples of Π.

Integration of Cot x Solved Examples

Below we have given some of the solved examples on the integration of Cot x. These examples will help students to understand this topic in a better way. These solved questions related to the integration of Cot x will help students securing good marks in the exam.

Example 1: Find the integral value of cot²x.

Solution: we have been given f(x) = cot²x

so, ∫f(x) dx = ∫cot²x dx

As, cosec²x = 1 + cot²x

so, cot²x = cosec²x – 1

substituting the above value in place of cot x, we get

∫cot²(x)dx = ∫(cosec²x−1)dx

or, ∫cosec²(x)dx − ∫1.dx

as ∫cosec²(x)dx = – cot x and ∫1.dx = x

= − cot x − x + C

Hence, ∫cot²x dx = − cot x − x + C

Example 2: Find the integration of cot 3x

Solution: given f(x) = cot 3x

so, ∫f(x) dx = ∫cot 3x dx   ——–(1)

we will use the substitution method of integration here

let 3x = t

Taking derivative on both sides

3 dx = dt

or, dx = dt/3

substituting the value of 3x and dx in equation (1)

∫f(x) dx = (1/3) ∫cot t dt

as we know by the integration of Cot x, ∫Cot x dx = ln | Sin x | + C

=>(1/3) ln | Sin t | + C

putting back t = 3x, we get

=> (1/3) ln | Sin 3x | + C

Hence, ∫cot 3x dx = (1/3) ln | Sin 3x | + C

Example 3: Evaluate ∫cot(x/2) dx.

Solution: Here we have been given the half angle of cot x

also, ∫f(x) dx = ∫cot(x/2) dx  ——– (1)

as we know that cot(x/2) can be written in the full-angle of another ratios.

i.e., cot(x/2) = cosec x + cot x

substituting the above value of cot(x/2) in equation 1, we get:

∫f(x) dx = ∫(cosec x + cot x) dx

or, ∫cosec x dx + ∫cot x dx ——–(2)

as we know ∫cosec x dx = ln | cosec x – cot x | + C

and by the integration of cot x formula, ∫cot x dx = ln | sin x | + C

substituting these results in equation (2), we get

∫f(x) dx = ln | cosec x – cot x | + ln | sin x | + C

Hence, ∫cot(x/2) dx = ln | cosec x – cot x | + ln | sin x | + C

Sharing is caring!