What are the different types or hexagon?

There are different types of hexagons, that are stated below. 1) Regular 2) Irregular 3) Convex 4) Concave

What is an Irregular Hexagon?

Those six-sided polygons that have at least two sides or two angles unequal in the measure are known by this name.

Pentagon is a closed 2D figure that has fives sides and five angles.

Those shapes or figures that have only two dimensions: length and breadth, are known as 2D shapes. They are flat shapes because of the absence of thickness or depth.

Can we obtain a hexagon by joining two shapes?

Yes, we can obtain this shape by joining two trapezoids having equal base lengths.

Hexagon- Definition, Types, Properties, Examples

Table of Contents

A hexagon is a closed figure with a definite number of sides and angles. It is one of the most fascinating polygons in the geometrical world. A polygon is basically a closed figure with at least 3 sides and 3 angles. As this geometrical shape observes all these properties, hence it is known as a polygon. It is one of the special types of polygons other than square, rectangle, pentagon, etc. It is a two-dimensional figure. In this article, we will explore the definition, types, properties, and some examples of this unique figure.

Hexagon

In the geometrical universe, a closed, two-dimensional object made up of six straight lines is referred to as a hexagon. Having six sides, six vertices, and six interior angles makes it a six-sided polygon. These are fascinating geometric forms with six sides and six angles that may be found in a variety of both natural and man-made constructions. Let us understand this special type of polygon by understanding its various aspects. But first of all, let us get acquainted with the definition and diagram (shape) of this special polygon.

Hexagon Definition

Formally, Hexagon is a two-dimensional (2D) closed polygon with six vertices and six line segments. In other words, any closed 2D figure made up of six line segments and six angles can be related to this special polygon. So, this geometrical shape has six sides and six angles, also known as six vertices. The sides and hence the angle of this polygon can be equal in measure or can have varying lengths. For any figure to qualify as this special polygon, it must satisfy the following criteria as per its definition:

It must be a closed 2D shape
It must have six sides and six angles

Hexagon Shape

The diagrammatic view of this shape will help you visualize and memorize this geometrical figure more easily. Through this diagram, you can also relate this shape to real-world objects. The shape of this special polygon is given below.

As we can see from the above figure that its shape is a closed 2D figure with six sides and six angles.

Hexagon Sides

As we can conclude from the above figure that the it has six sides in total. All the sides are joined together to form a closed shape. All the sides of this shape are straight edges, i.e., there is no curve anywhere in an edge. The shape of this geometrical figure can change depending on the measure of each side but the number of sides will always remain the same. The sum of all the sides of this polygon is known as its perimeter, like all other polygons. It has been classified into two categories based on its sides.

Hexagon Angles

The total number of angle existing in this special polygon is always six. It must be noted that its angles can be of same measure or of different measure. It consists of six interior angles as well as six exterior angles. The each corresponding interior-exterior angles exist in a pair. The sum of all the angles of this shape is equal to 720°. They are classified into two distinct categories based on the whether the measure of any of the interior angle is more than 180° or not.

Hexagon Types

There are different types of hexagon present in geometry, depending on the measure of sides and angles. The different types of this shape is listed below.

Regular: In this type, all the sides and all the angles equal in measure. So, all the interior angles of this type measure 120° each. The value of all the exterior angles of this type is 60°. That is, the sum of all the interior angles of this shape is 720° while the sum of all the exterior angles is 360°.
Irregular: These shapes have at least two sides and two angles with different measure. In other words, the value of each side and each angle is not equal. The sum total of all the angles will still remain 720°.
Concave: In this type, the measure of at least one of the angles is more than 180°. That is, in these types of special shape, a minimum of one angle will have a value more than 180 degree. We can easily recognize this type by observing its shape. At least one of the vertexes of this type will point inwards.
Convex: In this type, all of the inner angles are less than 180 degrees. They can have equal or unequal side lengths and angles depending on whether they are regular or irregular. One can recognize the shape of this type by noticing its vertices. Their vertices are all inclined towards the outside. The shapes given in the diagram above are of this category.

Hexagon Formula

There are many properties associated to this special polygon. As it is a closed figure, so we can find its perimeter and area. The formulas for area and perimeter is given below.

Perimeter

Perimeter is the total length of the edges of a closed polygon. The perimeter of this shape is given by:

a + b + c + d + e + f

where, a, b, c, d, e, and f are the measure of the six sides

Area

Area is the total space enclosed by the shape. The area of this geometrical shape is given by:

(perimeter x apothem)/2

where, apothem is the length of the center from the mid point of any side

Regular Hexagon

As stated above, a regular hexagon is a six-sided closed 2D shape that has all its angles and edges equal in value. That is, all the sides and angles of this type are equal. The shape of this special polygon is shown below.

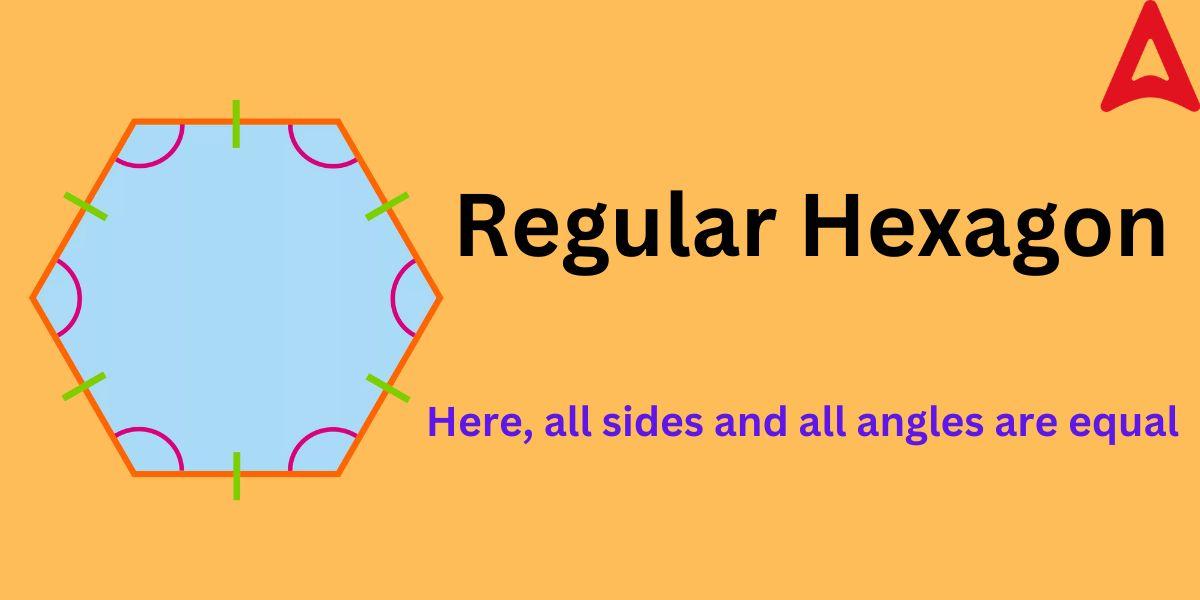
As shown in the above figure, all its sides are equal to each other and all its angles are equal too. The individual angle of this shape measures 120°. As all its sides are equal, so, the perimeter of this special type is given by 6X, where X is the length of the side. All the exterior angles of a triangle 60° each.

Hexagon Properties

The hexagon shows many properties that make it unique from other shapes. These unique properties will help students to identify these shapes from others. Some of its unique properties are given below:

It has six sides and six angles
The sum of all the angles is always equal to 720°
A total of 9 diagonals can be drawn in this polygon
The sum of exterior angles of a regular hexagon equals 360°
The area of this special type is equal to (3a²√3)/2, where a is the length of a side
It can be divided into 6 equilateral triangles of equal dimensions
Its opposite sides are always parallel to each other

Hexagon Real Life Examples

There are many real-life examples of a this shape available in the world. Some of the real-life examples of this polygon is given below:

Cross-section of a new pencil
Honeycomb
Football’s black colored spots
Nuts and Screws
Hexagonal Floor Tiles

Hexagon Solved Examples

Some of the solved questions on this topic is given below. These solved examples will help students understand this topic in a better way.

Example 1: If the sum of five angles of a hexagon is given to be 600°. Then what will be the measure of the sixth angle?

Solution: As we know that the sum of all the angles of a hexagon = 720°

So, 550° + sixth angle = 720°

sixth angle = 720° -550°

Hence, sixth angle = 170°

Example 2: If the perimeter of a regular hexagon is given to be 216 meter. Find the length of its sides.

Solution: As we know that,

Perimeter of a regular hexagon = 6X

where, X = length of the side

So, 6X = 216

X = 216/6

X = 36

Hence, the length of the side = 36

Example 3: If the area of one of one of the equilateral triangles of a regular hexagon is 16 m². Calculate the total area of that particular shape.

Solution: As we know there are 6 equilateral triangles in a regular hexagon

So, area = 6 x 16

Therefore, area = 96 m²