Heron’s Formula- Herons Formula Proof & Inventor

Heron’s Formula

Heron’s formula, named after the ancient Greek mathematician Hero of Alexandria, is used to calculate the area of a triangle when you know the lengths of all three sides. It’s a useful formula for finding the area of a triangle without knowing the height and base, which are typically required for other methods.

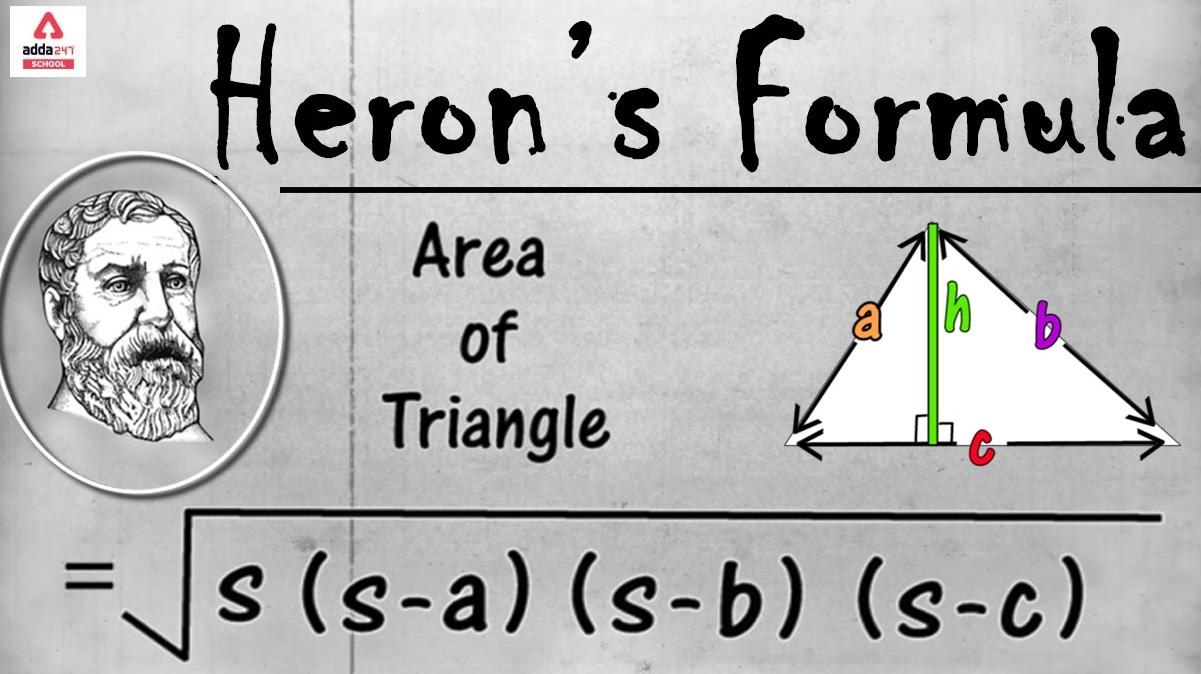
The Herons formula is as follows:

Let ‘a,’ ‘b,’ and ‘c’ be the lengths of the three sides of the triangle, and ‘s’ be the semi-perimeter of the triangle, which is half of the perimeter:

s = (a + b + c) / 2

Then, the area ‘A’ of the triangle can be calculated using Heron’s formula:

A = √(s * (s – a) * (s – b) * (s – c))

In this formula:

• ‘s’ is the semi-perimeter of the triangle.
• ‘a,’ ‘b,’ and ‘c’ are the lengths of the triangle’s sides.
• ‘A’ is the area of the triangle.

Heron’s formula is particularly useful when you have the lengths of the sides of a triangle but don’t have the altitude (height) or the base of the triangle readily available. It’s a straightforward way to calculate the area of a triangle using just the side length.

Heron’s Formula Definition

Heron’s formula (also known as Hero’s formula) gives the area of a triangle given the lengths of all three sides are known in geometry. It is named after Hero of Alexandria, who is the person to find the formula. Unlike previous triangle area formulas, no angles or other distances in the triangle must be calculated first.

Heron’s Formula Class 10

Metrica, Heron’s most important geometric work, was not discovered until 1896. It’s a three-volume compilation of geometric principles and formulas on areas and volumes of flat and solid forms that Heron compiled from a range of sources, some of which date back to ancient Babylon. The methods for calculating the area of various plane figures and the surface areas of common solids are listed in Volume I. A derivation of Heron’s (really, Archimedes’) formula for the area A of a triangle is included.

where a, b, and c are the lengths of the sides of the triangle, and s is one-half the triangle’s perimeter or

History of Heron’s Formula

Heron of Alexandria penned Heron’s formula about 60 CE. He was a Greek engineer and mathematician who calculated the area of a triangle using only the lengths of its sides and went on to calculate the areas of quadrilaterals using the same method. This formula was used to prove trigonometric laws such as the Laws of Cosines and the Laws of Cotangents.

Heron’s Formula Example

Heron’s formula is a mathematical formula that may be used to calculate the area of a triangle given its three side lengths. It can be used to any shape or type of triangle as long as the three side lengths are known. Hero’s Formula is another name for it. Also, it is not required to know a triangle’s angle measurement to compute its area.

According to Heron, the formula may be used to compute the area of any triangle, whether it is isosceles, equilateral, or scalene, given the sides of the triangle. Consider the triangle ABC, which has sides a, b, and c, respectively.

Proof of Heron’s Formula

Heron’s formula is a mathematical formula used to find the area of a triangle when you know the lengths of all three sides. It is named after the ancient Greek mathematician Hero of Alexandria but was known to mathematicians in India even earlier. The formula states:

Area (A) = √(s(s – a)(s – b)(s – c))

Where:

• A is the area of the triangle.
• a, b, and c are the lengths of the three sides of the triangle.
• s is the semi-perimeter of the triangle, which is calculated as s = (a + b + c) / 2.

Now, let’s prove Heron’s formula.

Heron’s Formula Proof

1. Start with a triangle with sides a, b, and c, and let s be the semi-perimeter, which is s = (a + b + c) / 2.
2. Draw an altitude (h) from one vertex of the triangle to the opposite side, splitting the triangle into two right triangles. Let’s call the segments of the base that the altitude divides it into, x and y.
3. Now, you have two right triangles: one with base x and height h and the other with base y and height h.
4. By the Pythagorean theorem, we can express the areas of both right triangles in terms of their bases and heights:

   Area1 = (1/2) * x * h Area2 = (1/2) * y * h

5. We can use the Pythagorean theorem to find the lengths x and y in terms of a, b, and c:

   x^2 + h^2 = a^2 (from the first right triangle) y^2 + h^2 = b^2 (from the second right triangle)

   Solving for x^2 and y^2: x^2 = a^2 – h^2 y^2 = b^2 – h^2

6. Now, we can add these two equations together to eliminate h^2:

   x^2 + y^2 = a^2 + b^2 – 2h^2

7. Since we know that c = x + y (because they form the base of the triangle), we can substitute x + y for c:

   x^2 + y^2 = a^2 + b^2 – 2h^2 = c^2 – 2h^2

8. Rearrange the equation to solve for h^2:

   2h^2 = c^2 – (a^2 + b^2)

9. Now, we can substitute h^2 back into the area formulas for the right triangles:

   Area1 = (1/2) * x * (c^2 – (a^2 + b^2)) / 2h Area2 = (1/2) * y * (c^2 – (a^2 + b^2)) / 2h

10. Simplify the expressions:

Area1 = (1/4h) * x * (c^2 – (a^2 + b^2)) Area2 = (1/4h) * y * (c^2 – (a^2 + b^2))

11. Add the areas of the two right triangles to find the area of the original triangle:

A = Area1 + Area2 A = (1/4h) * (x * (c^2 – (a^2 + b^2)) + y * (c^2 – (a^2 + b^2)))

12. Substitute x and y with expressions involving a, b, and c:

A = (1/4h) * ((c – y) * (c^2 – (a^2 + b^2)) + y * (c^2 – (a^2 + b^2)))

13. Since c – y = x, simplify further:

A = (1/4h) * (x * (c^2 – (a^2 + b^2)) + y * (c^2 – (a^2 + b^2))) A = (1/4h) * (x * c^2 – (a^2 + b^2) * x + y * c^2 – (a^2 + b^2) * y)

14. Now, remember that x^2 = a^2 – h^2 and y^2 = b^2 – h^2:

A = (1/4h) * ((a^2 – h^2) * c^2 – (a^2 + b^2) * (a^2 – h^2 + b^2 – h^2))

15. Simplify the expression:

A = (1/4h) * ((a^2 – h^2) * c^2 – (a^4 + b^4 – 2a^2b^2 – a^2h^2 – b^2h^2))

16. Now, substitute 2h^2 = c^2 – (a^2 + b^2) (from step 8):

A = (1/4h) * ((a^2 – h^2) * (a^2 + b^2 + 2h^2) – (a^4 + b^4 – 2a^2b^2 – a^2h^2 – b^2h^2))

17. Distribute and simplify:

A = (1/4h) * (a^2(a^2 + b^2 + 2h^2) – h^2(a^2 + b^2 + 2h^2) – a^4 – b^4 + 2a^2b^2)

18. Factor out (a^2 + b^2 + 2h^2):

A = (1/4h) * [(a^2 + b^2 + 2h^2)(a^2 – h^2 – b^2) – (a^4 + b^4 – 2a^2b^2)]

19. Notice that (a^2 – h^2 – b^2) is equal to -(c^2 – (a^2 + b^2) – b^2) and simplify further:

A = (1/4h) * [(a^2 + b^2 + 2h^2)(-c^2 + a^2 + b^2) – (a^4 + b^4 – 2a^2b^2)]

20. Now, substitute 2h^2 = c^2 – (a^2 + b^2) again:

A = (1/4h) * [(a^2 + b^2 + 2h^2)(-2h^2) – (a^4 + b^4 – 2a^2b^2)]

21. Simplify:

A = (-1/2h) * (h^2 – a^2 – b^2 + 2h^2 – a^4 – b^4 + 2a^2b^2)

22. Combine like terms:

A = (-1/2h) * (h^2 – a^2 – b^2 + 2h^2 – a^4 – b^4 + 2a^2b^2)

23. Now, we can cancel out some terms:

A = (-1/2h) * (h^2 – a^2 – b^2 + 2h^2 – a^4 – b^4 + 2a^2b^2) A = (-1/2h) * (h^2 + 2h^2 – a^2 – b^2 – a^4 – b^4 + 2a^2b^2)

24. Combine like terms again:

A = (-1/2h) * (3h^2 – (a^2 + b^2) – (a^4 + b^4 – 2a^2b^2))

25. Notice that a^4 + b^4 – 2a^2b^2 is a perfect square and can be factored as (a^2 – b^2)^2:

A = (-1/2h) * (3h^2 – (a^2 + b^2) – (a^2 – b^2)^2)

26. Simplify further:

A = (-1/2h) * (3h^2 – (a^2 + b^2) – (a^2 – b^2)^2)

27. Now, factor out 1/2h from the expression:

A = (1/2h) * ((a^2 + b^2) + (a^2 – b^2)^2 – 3h^2)

28. Substitute the value of 2h^2 from step 8:

A = (1/2h) * ((a^2 + b^2) + (a^2 – b^2)^2 – (c^2 – (a^2 + b^2)))

29. Simplify:

A = (1/2h) * (2(a^2 + b^2) – c^2)

30. Finally, cancel out the 2 in the numerator and denominator:

A = (a^2 + b^2 – c^2) / (2h)

31. But we know that h = √(s(s – a)(s – b)(s – c)), so substitute h back in:

A = (a^2 + b^2 – c^2) / (2 * √(s(s – a)(s – b)(s – c)))

32. This is the final expression of Heron’s formula:

A = √(s(s – a)(s – b)(s – c))

And there you have it! We have successfully derived Heron’s formula for finding the area of a triangle.

Heron’s Formula in Hindi

हीरोन का सूत्र

अलेक्जेंड्रिया का बगुला, जिसे हीरो के रूप में भी जाना जाता है, एक ग्रीक जियोमीटर और आविष्कारक था, जो मिस्र के अलेक्जेंड्रिया में 62 ईस्वी के आसपास रहता था, और जिसके लेखन ने बेबीलोनियाई, मिस्र और ग्रीको-रोमन गणित और इंजीनियरिंग के ज्ञान को भावी पीढ़ी के लिए संरक्षित किया था।

त्रिभुज के क्षेत्रफल के लिए हीरोन का सूत्र

मेट्रिका, हेरॉन का सबसे महत्वपूर्ण ज्यामितीय कार्य, 1896 तक खोजा नहीं गया था। यह ज्यामितीय सिद्धांतों और फ़ार्मुलों का तीन-खंडों का संकलन है, जो समतल और ठोस रूपों के क्षेत्रों और संस्करणों पर आधारित है, जिसे हेरॉन ने कई स्रोतों से संकलित किया है, जिनमें से कुछ प्राचीन काल के हैं। बेबीलोन। विभिन्न समतल आकृतियों के क्षेत्रफल और सामान्य ठोसों के पृष्ठीय क्षेत्रफलों की गणना करने की विधियाँ खंड I में सूचीबद्ध हैं। त्रिभुज के क्षेत्रफल A के लिए हीरोन (वास्तव में, आर्किमिडीज़) के सूत्र की व्युत्पत्ति शामिल है।

ए = √s(s−a)(s−b)(s−c)

जहां a, b, और c त्रिभुज की भुजाओं की लंबाई हैं, और s त्रिभुज की परिधि का आधा है या

एस = ए + बी +  सी

Heron Mathematician- Heron of Alexandria

Heron of Alexandria, also known as Hero of Alexandria, was a Greek mathematician, engineer, and inventor who lived around the first century AD. He is best known for his work in mathematics, engineering, and mechanics. Here’s a brief overview of his contributions and accomplishments:

1. Heron’s Formula: Heron is most famous for Heron’s formula, also known as Hero’s formula, which is used to find the area of a triangle when the lengths of all three sides are known. The formula is expressed as:Area = √(s * (s - a) * (s - b) * (s - c))

   Where s is the semi-perimeter of the triangle, and a, b, and c are the lengths of its sides.

2. Mechanical Inventions: Heron was an inventor and engineer, and he created a variety of mechanical devices. One of his most famous inventions was the aeolipile, which is considered one of the earliest examples of a steam engine. It consisted of a sphere mounted on a pair of tubes with nozzles that could be rotated. When the sphere was heated, steam would be expelled through the nozzles, causing the sphere to spin.
3. Pneumatics: Heron also made significant contributions to the field of pneumatics, the study of the mechanical properties of gases. He wrote a treatise called “Pneumatica,” in which he described various pneumatic devices and the principles behind them.
4. Automata: Heron is credited with designing and building several automata, which were mechanical devices that could perform tasks automatically. These included automated musical instruments and other novelty devices.
5. Geometry and Mathematics: In addition to Heron’s formula, he made contributions to geometry and mathematics in general. He wrote several works on mathematics and geometry, including “Metrica” and “Geometrica,” in which he discussed various geometric concepts and calculations.
6. Surveying and Mechanics: Heron’s work extended to practical applications in surveying and mechanics. He developed tools and techniques for measuring distances and angles, which were important for architectural and engineering projects of his time.

Heron’s works were influential in the development of mathematics and engineering, and many of his ideas and inventions laid the foundation for later advancements in these fields. While much of his work was lost to history, some of his writings were preserved and later rediscovered, contributing to our understanding of ancient Greek mathematics and technology.

Read More About:

• Colloidal Solution- Definition, Properties, Examples, Particle Size
• Endothermic Reaction – Definition, Equation, Examples, Formula
• Dielectric Constant- Definition, Formula, Meaning In Chemistry
• Limestone- Chemical Formula, Uses, Meaning
• Cannizzaro Reaction – Definition, Examples, Mechanism

Sharing is caring!