Cos 60 Degree Value

Cos 60 degree

The value of cos 60 degree is  (0.5 in decimal form) or 1/2. Trigonometry is used in right angled triangles to calculate parameters such as the length, height, and angle of the triangle.

Buy Online NEET 2022 Revision Course

There are six types of trigonometric functions which we use primarily. They are

• sine
• cosine
• tangent
• cotangent
• secant
• cosecant

The standard angles of the trigonometric ratios are 0°, 30°, 45° 60°, 90°.

Read about value of root 2 and square root of 2.

Cos 60 degree value

Trigonometric functions such as sine and cosine are used in the theory of periodic functions. These periodic functions are used to describe the light and sound waves. It is also used in oceanography to calculate the height of tides in oceans. Apart from these applications, trigonometry is also used by astronauts, physicists, and engineers.

Join Rapid Revision Course For JEE Main/Advanced 2022 Course

What is the value of cos 60 degree in fraction?

• The value of cos 60° is  (0.5 in decimal form).
• cos 60-degree fraction value is= 1/2 .
• You can also derive cos 60° value by having a look at the next section.

Value of Cos 60 degree

Follow the instructions given below to derive the value of cos 60°.

Consider a unit circle in the Cartesian plane. The plane can be divided into four quadrants. The cos 60° value takes place in the first quadrant.

90° – 30° = 60° (Equation 1)

sin (90° – a) = cos a (Trigonometric formula)

Now, we can write the value of cos 60° as,

sin (90° – 60°) = cos 60° (Using the trigonometric formula)

• sin 30° = cos 60° (Equation 2)

Since the value of sin 30° is , by substituting the value of sin 30° in equation 2 we get,

•  = cos 60°

Hence the value of cos 60° is .

Click Here To Free Study Meterial

Alternatively,

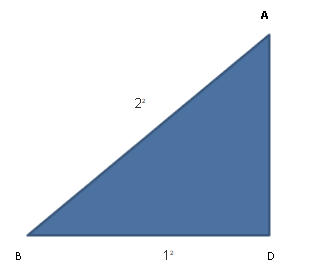
In right angled triangle ABD,

AB² = AD²+ BD²

2² = AD² + 1²

AD² = 2² -1²

AD² = 4 – 1

AD² = 3

AD = √3

Hence,

sin 60°  = AD/AB = √3/2

tan 60° =AD/BD =√3/1

cos 60°= 1/2

Read about table of 6. 

Cos 60 degree Value from Trigonometry Table

Trigonometric Angle Values

For the above triangle, we can determine the three angles namely sin, cos, and tan by using

sin =  Perpendicular/Hypotenuse

cos =  Base/Hypotenuse

tan = Perpendicular/Base

Read More Article Related To This

FAQs for Cos 60 degree value

What is the value cos 30°?

The value of cos 30 degree is  1/√2.

How do you find the value of sin 30°?

The value of sin 30 degree is 1/2

What is Cos squared of 60°?

Value of Cos 60 degree is  in fractional form and 0.5 in decimal form. (Cos 60)*(Cos 60) is . And in decimal form it will be 0.25.

What is trigonometry formula?

Trigonometry formula are the formulas which are used to solve the trigonometry problems in maths.

Sharing is caring!