Corresponding Angles

Corresponding Angles – Definition, Types, Properties and Solved Examples

When two parallel lines are intersected by traversal (third line), corresponding angles are formed in matching corners. Definition, properties, and examples of these special angles are given here.

Table of Contents

Corresponding angles are one of the crucial topics in geometry. It is primarily related to traversal lines and congruency. These angles are always congruent. You must have definitely heard the names of these angles in your high school mathematics. The concept of this special angle spans across each and every geometrical shape. So it is of utmost importance to understand the concept behind this crucial topic. This article will guide you through every small concept that you should know in order to master this domain of special angles.

As the name suggests, corresponding angles are those angles that is present in the corresponding or matching corners of the traversal. When two parallel lines are intersected by the transversal, these angles are created. Traversal are those lines which intersect the parallel lines. Along with these angles, other types of angles like vertically opposite angles and alternate angles are also created by this traversal. The concept of corresponding angle plays a huge role in solving many complex geometrical problems. Let us now understand this special type of angle in a detailed manner though its definition and an example.

Corresponding Angles Definition

Corresponding angles are pairs of angles that are in the same relative position at the junction of two lines and a transversal. Imagine a transversal (a line that intersects two or more other lines) passing through the intersection of two parallel lines to help you better grasp this. These special angles are those that are located in matching places, either on the same side of the transversal or on corresponding sides of the parallel lines. The following figurative example will give you a crystal clear view of the above-stated facts.

Corresponding Angles Examples

As we know, those angles can be termed corresponding in nature that are present in the corresponding or relative positions of the traversal. From the above figure, we can tell the names of these special angle pairs. Those are:

∠ 5 and ∠ 1

∠ 6 and ∠ 2

∠ 3 and ∠ 7

∠ 4 and ∠ 8

Corresponding Angles Types

These angles are classified into two types based on the nature of the two lines whom the traversal intersects. The two lines intersected by the traversal can either be parallel or non- parallel. Parallel lines are those lines which always remain equidistant from each other. Based on this, the two types are:

Corresponding angles created by a traversal and two parallel lines
Corresponding angles created by a traversal and two non-parallel lines

It should be kept in mind that the these angles created by a traversal and two non-parallel lines are not too much related in property. They are just corresponding due to their relative position. So most of the times, we study about the the other type, i.e., angles created by a traversal and two parallel lines.

Corresponding Angles in a Triangle

In a triangle, the concept of these angles is related with congruency of triangles. These angles are present in triangles only if they are congruent. In a congruent triangle, two angles are said to be corresponding in nature if they are equal in measure. In other words, the angle formed by two pairs of congruent sides of congruent triangles are known as corresponding angles in a triangle. Let us clearly explore this concept through a diagram.

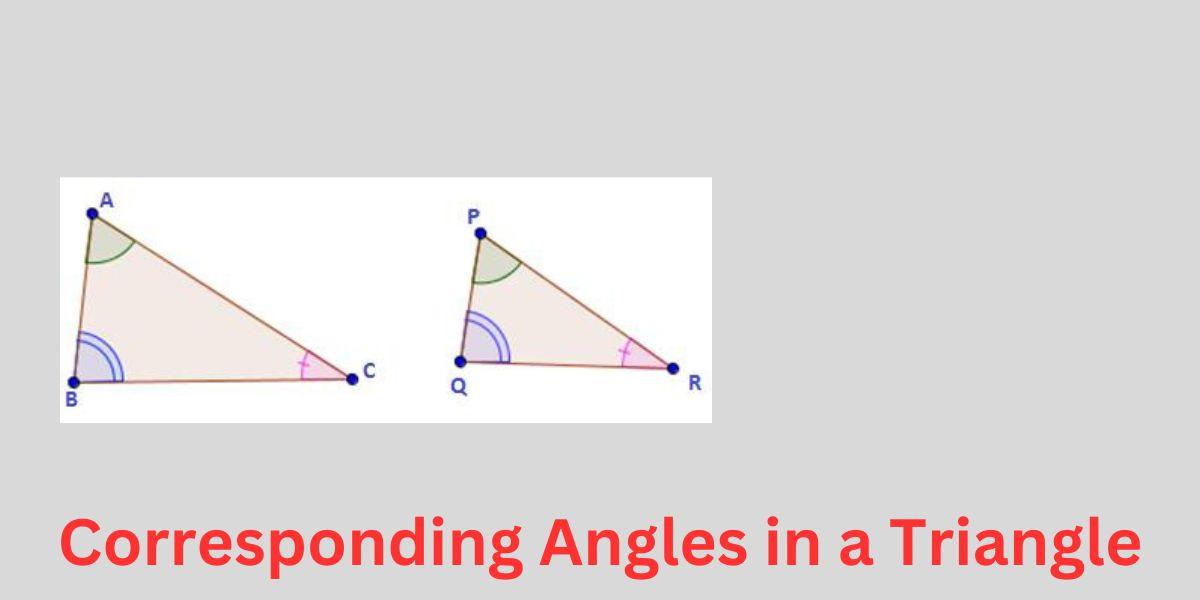
In the above figure, ΔABC is congruent to ΔPQR

Hence, the corresponding pairs of angle are:

∠A = ∠P

∠B = ∠Q

∠C = ∠R

Corresponding Angles Property

These angles show many different properties which help them identify from rest of the angles. These important properties of these special angles will prove to be beneficial for solving problems.

They always occur in pairs
These angles are formed by parallel lines and a traversal are always congruent or equal in measure
These angles created by traversal and non-parallel lines are not congruent
They are situated on the same side of the traversal
They are also present in congruent triangles
The congruent triangles’ corresponding angles are equal in measure

Corresponding Angles Theorem

The theorem for this special angle states that “If a line intersects two parallel lines, then the corresponding angles are congruent (equal)”. It is also sometime referred to as the “corresponding angles postulate”. The converse of the theorem also hold true. That is, if angles that are corresponding in position are congruent (equal in measure), then the two lines must be parallel.

Corresponding Angle Solved Examples

Below we have mentioned some solved examples of these angles, so that students can get a better understanding about how to solve the problems related to these special angles.

Example 1: Given that angle A and angle B are corresponding in nature. If the value of angle A is 70°, then what will be the value of angle B?

Solution: As we know that angles that are corresponding are congruent in nature

Hence, angle A = angle B

Therefore, ∠B= 70°

So the value of angle B will also be 70°.

Example 2: You are given two angles: ∠A and ∠B. These angles are located at corresponding positions. The values ∠A and ∠B are 6y + 3 and 2y – 5 respectively. What will be the value of y?

Solution: Here we are given two angles A and B that are corresponding in nature

By using the property of corresponding angles, we can say that

∠A = ∠B

So, 6y + 3 = 2y -5

=> 6y -2y = -5 -3

=> 4y = -8

=> y = -8/4

=> y = -2

Hence, the value of y will be 2.

Example 3: There are two congruent triangles ΔPQR and ΔXYZ. We are given the measurements of two angles of ΔPQR, which are ∠P = 70° and ∠Q= 30°. Find out the value of ∠Z.

Solution: We have been given,

∠P = 70°

∠Q = 30°

ΔPQR ≅ ΔXYZ

Hence the angles at corresponding positions of both these triangles will be equal

So, ∠P = ∠X = 70°

∠Q = ∠Y = 30°

By applying the angle sum rule of a triangle here,

∠X + ∠Y + ∠Z = 180°

70° + 30° + ∠Z = 180°

100° + ∠Z = 180°

∠Z = 180° – 100°

∠Z = 80°

Example 4: The values of two angles that are corresponding in nature are given to be 5P – 10 and 60. What will be the value of P?

Solution: Given, 5P – 10 and 60 are corresponding in nature, so the measure of their angles will be equal

i.e., 5P – 10 = 60

=> 5P = 60 + 10

=> 5P = 70

=> P = 70/5

P = 14

FAQs

What are Corresponding angles?

Corresponding are those angles that are created in relative positions or matching corners when two lines are intersected by the third line known as traversal. Corresponding angles are created on the related places on the same side with traversal.

Are corresponding angles always congruent?

Yes, they are always congruent in the case of parallel lines. They may not be congruent when the intersected lines are non-parallel

Can corresponding angles ever form a supplementary pair?

Yes, they can be supplementary when the traversal intersects the parallel lines at 90°, i.e., perpendicularly. In this case, each corresponding angle measures 90° and the corresponding pairs form supplementary angles.