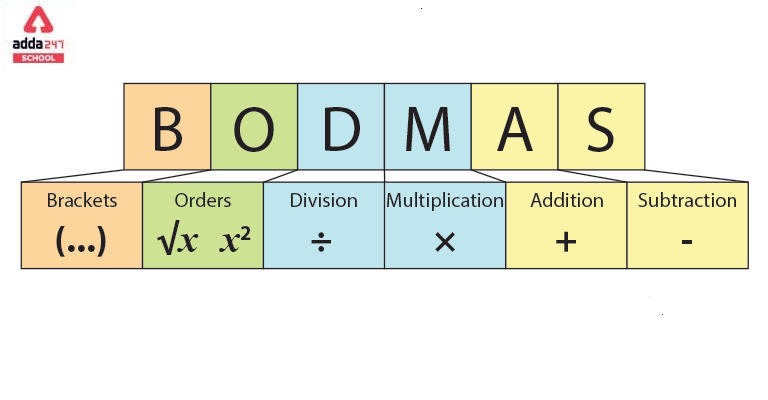
BODMAS Full Form in Mathematics With Sign, Examples, Order

Q: What is the use of Bodmas rule?

It helps in simplification of mathematical expression with accuracy. With the help of Bodmas, we don't miss out on the steps and can carry out the correct answer easily.

Table of Contents

BODMAS Full Form in Mathematics

BODMAS rule stands for the bracket, order, division, multiplication, addition, and subtraction. It is used to solve mathematical expression that consists of complex equations including addition, subtraction, multiplication, division, bracket, and order.

BODMAS gives the right order to solve mathematical equations without missing any step. According to the BODMAS rule, to solve any equation, we should first evaluate the brackets and solve anything inside them. After bracket, evaluate the powers, roots, or exponents. All the calculations are done from left to right. Then evaluate the equation for division and multiplication and then followed by addition and subtraction. Here, addition and subtraction are of the same priority, so, you can choose to do addition first or subtraction first. The same goes with multiplication and division, you can which one to do first.

Full form of BODMAS with sign in Maths

BODMAS consists of the first letter of the operations involved in a mathematical equation.

B- Bracket (), [], {}

O- Order, Square root, exponents, and powers

D- Division, ÷ /

M- Multiplication × *

A – Addition +

S – Subtraction –

Here, we can see there are three types of brackets, how will you decide, which bracket to solve first? Brackets within brackets are very complex equations, different bracket implies different part of the equation.

Bracket	Name
( )	Parentheses
[]	Brackets or square brackets
{ }	Braces or Curly bracket

Parentheses are the innermost bracket in any equation, followed by braces and square brackets. Carry out the required operations in the parentheses first, then with basic mathematical calculation remove the brackets. If there is no sign between the brackets, it implies multiplication. Similarly, evaluate the braces and the square brackets.

BODMAS Full Form in Computer

BODMAS rule was invented by Archillies Resefelt. He was a mathematician. He made it into a mnemonic that can be remembered easily, he made the First Letter of the operation into a word so that we can remember it and carry out calculations easily. The BODMAS rule determines the order of the equation.

Concept of BODMAS

In any mathematical expression or any equation, there are two components, numbers, and operations.

Numbers – A number is a mathematical component or value which represents the quantity and it is generally used for counting and calculations. Numerals are the symbols that represent numbers.

These are classifications of numbers

natural numbers
irrational numbers
rational number
real numbers
whole numbers
integers
complex numbers

Operations- those are the characters that combine numbers and form equation

These operations are used in mathematics

addition
subtraction
division
multiplication

These numbers and operations make complex equations which also includes fraction and orders, to solve these equations we need to follow the correct steps to find the correct answer. With the use of BODMAS, we can calculate the correct answer with the correct sequence.

Related Post:

BODMAS Full Form in Hindi

बोडमास नियम का आविष्कार आर्चिलीज रेसेफेल्ट ने किया था। वह एक गणितज्ञ थे। उन्होंने इसे एक स्मृतिचिह्न बनाया जिसे आसानी से याद किया जा सकता है, उन्होंने ऑपरेशन के पहले अक्षर को एक शब्द में बनाया ताकि हम इसे याद रख सकें और गणना आसानी से कर सकें। BODMAS नियम समीकरण के क्रम को निर्धारित करता है।

बोडमास की अवधारणा

किसी भी गणितीय व्यंजक या किसी समीकरण में दो घटक, संख्याएँ और संक्रियाएँ होती हैं।

संख्याएँ – एक संख्या एक गणितीय घटक या मान है जो मात्रा का प्रतिनिधित्व करता है और इसका उपयोग आमतौर पर गिनती और गणना के लिए किया जाता है। अंक वे प्रतीक हैं जो संख्याओं का प्रतिनिधित्व करते हैं।

ये संख्याओं के वर्गीकरण हैं

प्राकृतिक संख्याएं
तर्कहीन संख्या
परिमेय संख्या
वास्तविक संख्या
पूर्ण संख्याएं
पूर्णांकों
जटिल आंकड़े

संक्रियाएँ- वे वर्ण हैं जो संख्याओं को जोड़ते हैं और समीकरण बनाते हैं

इन संक्रियाओं का उपयोग गणित में किया जाता है

योग
घटाव
विभाजन
गुणा

ये संख्याएँ और संक्रियाएँ जटिल समीकरण बनाती हैं जिनमें भिन्न और क्रम भी शामिल हैं, इन समीकरणों को हल करने के लिए हमें सही उत्तर खोजने के लिए सही चरणों का पालन करने की आवश्यकता है। बोडमास के प्रयोग से हम सही क्रम के साथ सही उत्तर की गणना कर सकते हैं।

BODMAS Order Problems with Examples

Let’s carry out an expression step by step by using the BODMAS rule.

Question– 6 x (3 x 3²) ÷ 3+5 – 6 =?

Solution –

Step 1. Brackets ()

The equation in the bracket is (3 x 3²), according to the BODMAS rule, first solve the bracket.

3 × 3² – here, solve the order, which is 32

3²= 9

Now, we have 3×9= 27

Therefore, the equation becomes 6×27÷ 3+5 – 6 =?

Step 2. Division and multiplication ÷ ×

Carry out both division and multiplication in the equation. Start the calculation from left to right

6×27= 162

162÷3= 54

Now, the equation we get is 54+5-6=?

Step 3. Addition and subtraction + –

Same as above follow the left to right order for calculation.

Add and subtract the equation,

54+5= 59

59-6= 53

The answer is 53.

Hence, 6 x (3 x 32) ÷ 3+5 – 6 = 53

Sample questions

Level I

Simply:
12+(9+6×4)

Solution –

12+ (9+24)

= 12+ 33

= 45

(8+4-7+3) ÷2

Solution-

= (12-10) ÷2

=2÷2

5×3-4+6(without bracket)

Multiple first

5×3 = 15

Then addition

4+6= 10

Next, subtract,

15-10= 5

Level II

Simply:
500÷ [10{(15-12) + (12-10)}]

First, Simplify {} and operate the equation inside it

= 500 ÷ [10{3+2}]

= 500÷ [10{5}]

Now, simplify []

=500÷50

= 10

1/4{6[(12+4) – (10+2)]}

Simply (), followed by [] and {}

=1/4{6[16-12])

= 1/4{6[4]}

=1/4{24}

= 6

Level III

Simply
1/2- (6/4 of 3/6) + 1/4

1/2-(6/4 × 3/6) + 1/4

=1/2-3/4-1/4

= 12-9-6/24

= 12-3/24

=9/24= 3/8

BODMAS Full Form- FAQ

What is the full form of Bodmas?

A. Bodmas stands for the bracket, order, division, multiplication, addition, and subtraction.

2. What is the difference between Bodmas and Pemdas?

A. The difference between Bodmas and Pemdas is Bodmas stands for the bracket, order, division, multiplication, addition, and subtraction and Pemdas stands for Parentheses, Exponents, division, multiplication, addition, and subtraction.

3. What is the use of Bodmas rule?

A. It helps in the simplification of mathematical expressions with accuracy. With the help of Bodmas, we don’t miss out on the steps and can carry out the correct answer easily.

4. What are the arithmetic operations used in the BODMAS rule?

A. The arithmetic operations used in the BODMAS rule are division, multiplication, square root, addition, and subtraction.

5. Can the BODMAS rule be used to solve the expression without a bracket?

A. Yes, the BODMAS rule can be applied to the expression without a bracket.