Area of Square Formula for Class 7 with Examples

Area of Square

Area of Square: In geometry, Area is described as the Region or space occupied by the figure. The Area of Square, like other geometrical figures, is the space enclosed by the square’s boundary. In other terms, the number of square units required to fill a square is specified as the area of square. The measurement of the area is done by the Area of Square Formula. In this article, we are going to learn about the Area of Square Formula and its derivation with some solved Examples.

What is Area of Square

Squares can be seen almost anywhere in our daily lives. Some common examples of square-shaped objects square are Dice, chessboards, Rubic cubes, and so on, Before going into the area of square in detail, Let’s take a brief Idea of Square and its properties. A square is a closed two-dimensional geometry with four equal sides and four equal 90-degree angles. The four angles at the vertices are produced by the four sides of the square. A square’s perimeter is the sum of the total lengths of its sides, and its area is the total space occupied by the shape.

Area of Square Formula for Class 7,8,9

The area of a square is the space occupied inside its boundary. The area of a square will be obtained by multiplying two side lengths of that given square. Although while using the area of square formula  We consider the length of a square’s side as all of the sides of the shape are equal,  When the side is given, the formula for calculating the area of square is:

The area of square Formula can be written as A= Side × Side =(side)² square units

Let us now apply this area of square formula to calculate the area square which has a side length of 10 units.

Area of Square formula is A= Side × Side =(side)²

So, the area of the given square is = 10×10  =(10)²= 100 square units.

Area of Square Formula Unit

From the Area of square formula, we can conclude that the Area of a square equals the product of its two sides. We know that the Length of a figure is always expected in Units such as Cm, meters, inches, etc. As we obtain the area of a square by multiplying two sides, the units is used to denote the area of square in square units. As we see Area of square can be measured in a variety of units. The most popular units for measuring square area are square meters, square feet, square inches, and square cm.

some conversions for transforming standard measures of the area to other units are provided below:

• 1 m = 100 cm
• 1 sq. m = 10,000 sq. cm
• 1 km = 1000 m
• 1 sq. km = 1,000,000 sq. m

Area of Square Formula Derivation

Let us look at the derivation of the area of square formula to gain a better understanding of the formula. A square is a closed quadrilateral with four sides, as defined by its attributes. Thus, a square is a four-sided figure with equal sides.

The formula we use to find the area of a rectangle is = Length × breadth = L × B

Consider a square with a unit length and a unit breadth (all the sides are equal in a Square)

As a result, we express the area of the square as A=a×b=a×a=a²

Hence, The Area of Square formula = Side × Side =(side)² unit²

Area of Square Formula using Diagonals

The area of the square can also be determined with the help of signals of the square if the length of a side is unknown.

Let us examine the formula’s derivation using the diagram below, where ‘d’ represents the diagonal and “a” represents the square’s sides.

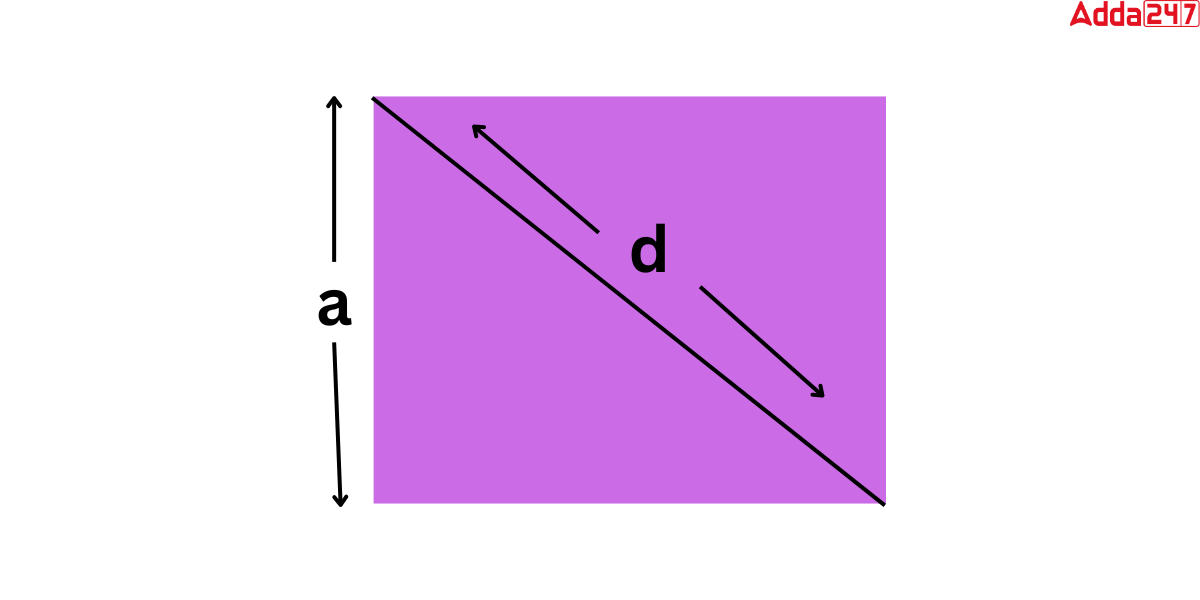In this case, using Pythagoras’ theorem,
we get that d² = a² + s²
d² = 2a²
a = d/2.
This formula of the length of one side of a square formula will now assist us in determining the area of square using the diagonal.
Area of Square formula = Side × Side =(side)² =a²
Now, Area = a² = (d/2)² = d²/2.
As a result, When the diagonal is known, the formula for calculating the area of square is:

Area of a square using diagonals = Diagonal²/2.

What is the Formula for the Area of a Square Example?

Example 1: Determine the area of a square having a side length of 9 cm.
Solution:

The given Side lenth of the square = 9 cm

We know that, Area of a square = Side²

Hence, Area of the square = 9² = 9 × 9 = 81 cm²

Example 2 : Determine the area of a square with a diagonal of 10 cm.

Solution:

The length of the Diagonal of the given square = 10 cm

We know that the formula for the area of a square when a diagonal is specified is = d²/2.

Hence, Area of the square = (10 × 10)/2 = 50 cm².

Sharing is caring!