0 Factorial
The factorial function, denoted by n!, plays a vital role in various areas of mathematics, particularly combinatorics. It represents the product of all positive integers less than or equal to n. For instance, 4! (factorial of 4) is calculated as 4 x 3 x 2 x 1 = 24. However, a question arises: what is the factorial of 0?
Zero Factorial
Intuitively, it might seem like multiplying no numbers would result in zero. But within the mathematical framework, zero factorial (0!) is defined as 1. This concept might seem counterintuitive, so let’s delve into the reasoning behind it and explore different approaches to understanding 0!.
The Recursive Definition of Factorial:
A common way to define factorials is recursively:
n! = n * (n-1)!
This definition states that the factorial of a number is the product of itself and the factorial of the preceding number. For example, using this definition:
3! = 3 * 2! = 3 * (2 * 1!) = 3 * (2 * 1) = 6
Factorial of Zero in Simple words
If we try to apply the recursive definition to 0!, we get:
0! = 0 * (-1)!
Here, we encounter a problem. Factorials are typically defined only for non-negative integers. A negative factorial isn’t mathematically defined. This roadblock suggests we need an alternative approach to understanding 0!.
Empty Arrangements and the Value of 1
Imagine you have zero objects to arrange. How many unique arrangements are there? The answer is simply one. There’s only one way to arrange nothing – by doing nothing at all! This concept aligns with the idea of 0! representing the number of ways to arrange zero items. Since there’s only one way (doing nothing), 0! is assigned the value of 1.
Combinations and the Empty Set
Factorials also find application in calculating combinations. Combinations refer to the selection of items from a set, where order doesn’t matter. Let’s consider a scenario where we have a set containing zero elements (the empty set). How many ways can we choose zero elements from this set? Again, there’s only one way – selecting none of the elements (the empty set itself). This aligns with the notion of 0! being 1, representing the single valid combination when dealing with an empty set.
Avoiding Zero in the Product
The standard definition of factorial (n! = n x (n-1) x … x 1) multiplies consecutive positive numbers down to 1. If we include zero in this product, we would encounter another issue. Multiplying by zero would always result in zero, regardless of the other factors. To maintain consistency and avoid this issue, mathematicians define 0! as 1, effectively skipping zero in the product altogether.
What is the value of 0 Factorial?
While initially counterintuitive, assigning a value of 1 to 0! serves a crucial purpose within the mathematical framework. This definition ensures consistency with the recursive definition of factorials and facilitates applications in combinatorics, particularly when dealing with empty sets or arrangements. By understanding the logic behind 0! = 1, we gain a deeper appreciation for the elegance and coherence of mathematical concepts.

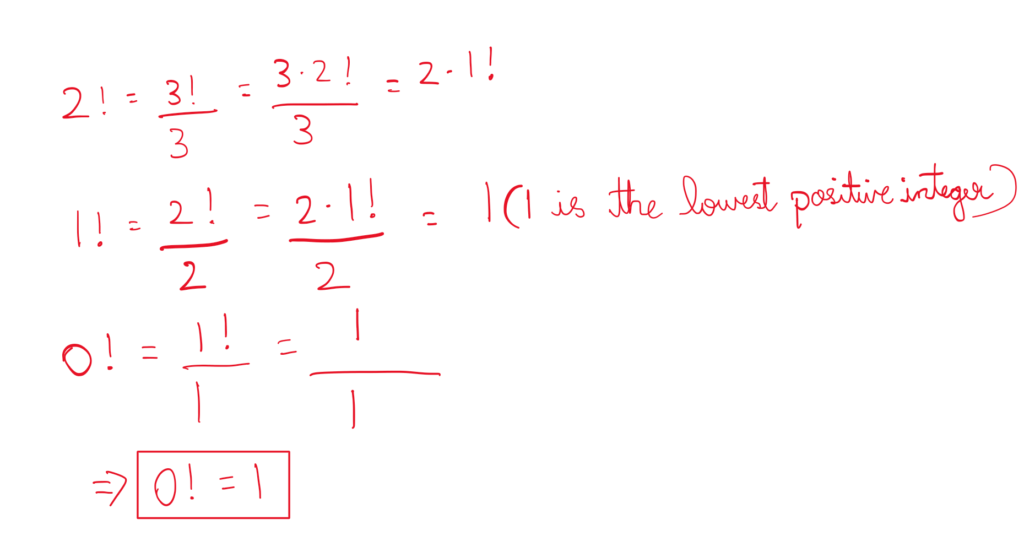







 Jawahar Navodaya Vidyalaya Admission For...
Jawahar Navodaya Vidyalaya Admission For...
 Karnataka DCET Seat Allotment Result 202...
Karnataka DCET Seat Allotment Result 202...
 AP POLYCET Seat Allotment Result 2025 OU...
AP POLYCET Seat Allotment Result 2025 OU...









