Maths Formulas
The notification for various defence exams like NDA, CDS, AFCAT, AGNIVEER is released and in competitive exams other defence-related tests, the Quantitative Aptitude section holds great importance. Regular practice in problem-solving techniques is important for success, which helps in gaining high scores. This article provides a overview of essential topics and Maths Formulas in Quantitative Aptitude for effective preparation. By mastering these topics and formulas, candidates can significantly enhance their preparation and increase the chance’s of achieving the goal in their chosen defence examinations. Also, an attached PDF with math formulae is provided a the end of the article to help the aspirants in a better way,
Maths Formulas for Defence Exams
While the Quantitative Aptitude section in exams may present diverse question formats, they all rely on a consistent set of formulas and problem-solving approaches. Developing a solid understanding of these formulas and techniques is important for effectively solving questions, especially under time limits. With a strong grasp of fundamental concepts, this section becomes an excellent opportunity to boost overall scores. To help in mastering this section, we have provided key math topics and formulas for comprehensive preparation.
List of Important Mathematics Formulas
Given below are the important topics that you need to cover in order to score good marks in mathematics. We have also provided you with the PDF for every part so that you could practice chapter-wise by applying the required formulas –
1. Speed, Distance & Time
This concept has been asked the most in all sorts of competitive exams especially in Defence exams and it is also considered to be one of the easiest topics to deal with. However, the type of questions asked in the examinations may have a different variety. But we have provided you with all formulae related to it which will help you to solve every problem related to Speed, distance and time.
- 1 Kmph = (5/18) m/s
- 1 m/s = (18/5) Kmph
- Speed(S) = Distance(d)/Time(t)
- Average Speed = Total distance/Total Time = (d1+d2)/(t1+t2)
- When d1 = d2, Average Speed = 2S1S2/(S1+S2), where S1 and S2 are the speeds for covering d1 and d2 respectively.
- When t1 = t2, Average Speed = (S1+S2)/2, where S1 and S2 are the speeds during t1 and t2 respectively.
- Relative speed when moving in the opposite direction is S1+S2
- Relative speed when moving in the same direction is S1-S2
- A person goes a certain distance (A to B) at a speed of S1 kmph and returns back (B to A) at a speed of S2 kmph. If he takes T hours in all, the distance between A and B is T(S1S2/(S1+S2)
- When two trains of lengths l1 and l2 respectively travelling at the speeds of S1 & S2 respectively cross each other in time t, then the equation is given as S1+S2 = (l1+l2)/t
- When a train of length l1 travelling at a speed of S1 overtakes another train of length l2 travelling at speed S2 in time t, then the equation is given as S1-S2 = (l1+l2)/t
- When a train of length l1 travelling at a speed of S1 crosses a platform/bridge/tunnel of length l2 in time t, then the equation is given as S1 = (l1+l2)/t
- When a train of lengths l travelling at a speed s crosses a pole/pillar/flag post in time t, then the equation is given as s = l/t
- If two persons A and B start at the same time from two points P and Q towards each other and after crossing they take T1 and T2 hours in reaching Q and P respectively, then (A’s speed) / (B’s speed) = √T2 / √T1
2. Profit & Loss
The profit and Loss formula is used to find out the price of an item and to know how profitable a business is. Every product has a cost price at which an item is purchased and a selling price at which an item is sold and based on the values of these prices, you can easily find out the profit gained or loss incurred on a particular product. Using the formulas given below you can find out the answers to such problems easily –
- Profit, P = SP – CP; SP>CP
- Loss, L = CP – SP; CP>SP
- P% = (P/CP) x 100
- L% = (L/CP) x 100
- SP = [(100 + P%)/100] x CP
- SP = [(100 – L%)/100] x CP
- CP = [100/(100 + P%)] x SP
- CP = [100/(100 – L%)] x SP
- Discount = MP – SP
- SP = MP -Discount
- If P% and L% are equal then, %loss = P2/100
- When the profit is x% and loss is y%, then the net % profit or loss will be: (x-y-xy)/100
- If a product is sold at x% profit and then again sold at y% profit then the actual cost price of the product will be: CP = [100 x 100 x P/(100+x)(100+y)]. In case of loss, CP = [100 x 100 x P/(100-x)(100-y)]
- For false weight, profit percentage will be P% = (True weight – false weight/ false weight) x 100
- When there are two successful profits say x% and y%, then the net percentage profit equals (x+y+xy)/100
3. Percentage
Percentage means per hundred. Percentages are a portion or fraction of 100 and it is denoted by the symbol ‘%’, the percentage is majorly used to compare and find out ratios. The percentage is an interesting and a scoring topic. Once you understand the basics, it becomes easier to solve problems related to percentage –
- To calculate the percentage of a fraction we have to use the given formula. Percentage formula = (Numerator/Denominator) ×100
- To calculate the percentage of a Number. Percentage /100* Number
- To express x% as a fraction. X%/100. To express % as a Fraction, we need to just divide it by 100.
- To Increase A value or Number by a Given Percentage. Number * 100+x%/100
- To Decrease A value or Number by Given Percentage. Number * 100-x%/100
- To calculate the percentage Decrement of a number. Percentage Decreament = Initial value-Final value/ Initial value*100
- To calculate the percentage increment of a number. Percentage Increament = Final value – Initial value/ Initial value*100
- If X% of A is equal to Y% of B. Z% of A = y*z/x% of B
- If the passing marks in an examination is P%. If a candidate scores S marks and fails by F marks then Maximum Marks will be. Maximum Marks = 100*P+S/P
- If a candidate scores marks and fails by A marks while another candidate scores y% marks and gets B marks more than minimum passing marks, then Maximum Marks will be. Maximum Marks = Sum of score *100/Difference in % Marks
- If the price of an item decreases, a person can buy a few Kg more in Y rupees, the actual price of that item. Actual Price = Rate * Y/100- Rate*X Per Kg
- If the population of a town is P and it increases at the rate of R% per annum then –Population after ‘n’ years : Percentage population = P x (1 + R/100)n
- If the population of a town is P and it decreases at the rate of R% per annum then –Population after ‘n’ years : Percentage population = P x (1 – R/100)n
- If the population of a town is P and it increases at the rate of R% per annum then –Population of the town ‘n’ years ago : Population n years ago = P/(1 + R/100)n
- If the population of a town is P and it decreases at the rate of R% per annum then –Population of the town ‘n’ years ago: Population n years ago = P/(1 – R/100)n
- Cost of Machine: Value of Machine After n years = P x (1 – R/100)n. Value of Machine Before n years = P/(1 – R/100)n
4. Average
Averages can be defined as the central value in a set of data. Average can be calculated simply by dividing the sum of all values in a set by the total number of values. In other words, an average value represents the middle value of a data set. The data set can be of anything like age, money, runs, etc.
- Average = Sum of quantities/ Number of quantities
- Sum of quantities = Average * Number of quantities
- The average of first n natural numbers is (n +1) / 2
- The average of the squares of first n natural numbers is (n +1)(2n+1 ) / 6
- The average of cubes of first n natural numbers is n(n+1)2 / 4
- The average of the first n odd numbers is given by (last odd number +1) / 2
- The average of first n even numbers is given by (last even number + 2) / 2
- The average of squares of first n consecutive even numbers is 2(n+1)(2n+1) / 3
- The average of squares of consecutive even numbers till n is (n+1)(n+2) / 3
- The average of squares of squares of consecutive odd numbers till n is n(n+2) / 3
- If the average of n consecutive numbers is m, then the difference between the smallest and the largest number is 2(m-1)
- If the number of quantities in two groups be n1 and n2 and their average is x and y respectively, the combined average is (n1x+n2y) / (n1+ n2)
- The average of n quantities is equal to x. When a quantity is removed, the average becomes y.
The value of the removed quantity is n(x-y) + y - The average of n quantities is equal to x. When a quantity is added, the average becomes y.
The value of the new quantity is n(y-x) + y
5. Algebra
Algebra is a very important section for all competitive exams. It can be a tricky part to solve but using these given formulas you can ace it in this section. Here we are going to mention the list of some important formulas of algebra that will certainly help you to solve Algebra problems
- a² – b² = (a-b)(a+b)
- (a+b)² = a² + 2ab + b²
- (a-b)² = a² – 2ab + b²
- a² + b² = (a-b)² +2ab
- (a+b+c)² = a²+b²+c²+2ab+2ac+2bc
- (a-b-c)² = a²+b²+c²-2ab-2ac+2bc
- a³-b³ = (a-b) (a² + ab + b²)
- a³+b³ = (a+b) (a² – ab + b²)
- (a+b)³ = a³+ 3a²b + 3ab² + b³
- (a-b)³ = a³- 3a²b + 3ab² – b³
- “n” is a natural number, and – bn = (a-b) (an-1 + an-2b +….bn-2a + bn-1)
- “n” is an even number, an + bn = (a+b) (an-1 – an-2b +….+ bn-2a – bn-1)
- “n” is an odd number an + bn = (a-b) (an-1 – an-2b +…. – bn-2a + bn-1)
- (am)(an) = am+n (ab)m = amn
6. Partnership
When more than one person invests their money to run a business or firm then this kind of agreement is called partnership. Involved parties in partnership are called partners.
There are two types of partners.
- Sleeping Partner: Sleeping partner is the person who provides only investment but does not take part in running the business.
- Working Partner: Working partner is the person who not only invests the money but also takes part in running the business. For this work, he is paid some salary or some percent of profit in addition.
If two partners A and B are investing their money to run a business then (Simple Partnership)
Capital of A/Capital of B = Profit of A/Profit of B
Capital of A : Capital of B = Profit of A : Profit of B
If two partners A and B are investing their money for different period of time to run a business then (Compound Partnership)
Capital of A * Time Period of A/Capital of B* Time Period of B = Profit of A/Profit of B
Capital of A × Time period of A : Capital of B × Time period of B = Profit of A : Profit of B
7. Time, Work & Wages
When you know Time, Work and wages formula, you can completely link that formula to the solution as soon as you read the question. Knowing Time, Work and wages tricks will also help you solve the questions in a few seconds and thus saving your time for other sections. You can find Time & Work formulas along with important Time & Work Tricks below.
- Wages are given in proportion to the work done and in indirect (or inverse) proportion to the time taken by the individual.
Total Wage = Total number of days × Wage of 1 day of a person · - Work Done = Time Taken × Rate of Work
- Rate of Work = 1 / Time Taken
- Time Taken = 1 / Rate of Work
- If a piece of work is done in x number of days, then the work done in one day = 1/x
- Total Work Done = Number of Days × Efficiency
- Efficiency and Time are inversely proportional to each other
- X:y is the ratio of the number of men who are required to complete a piece of work, then the ratio of the time taken by them to complete the work will be y:x
- If x number of people can do W1 work, in D1 days, working T1 hours each day and the number of people can do W2 work, in D2 days, working T2 hours each day, then the relation between them will be
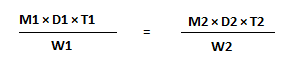
8. LCM and HCF
LCM i.e. least common multiple is a number which is a multiple of two or more than two numbers. For example: The common multiples of 3 and 4 are 12, 24 and so on. Therefore, l.c.m.is smallest positive number that is multiple of both. Here, l.c.m. is 12. HCF i.e. highest common factor are those integral values of number that can divide that number. LCM and HCF problems are very important part of all competitive exams.
Product of two numbers = Their h.c.f. * Their l.c.m.
2) h.c.f. of given numbers always divides their l.c.m.
3) h.c.f. of given fractions = h.c.f. of numerator
l.c.m. of denominator
4) l.c.m. of given fractions = l.c.m. of numerator
h.c.f. of denominator
5) If d is the h.c.f. of two positive integer a and b, then there exist unique integer m and n, such that d = am + bn
6) If p is prime and a,b are any integer then P ,This implies P or P ab a b
7) h.c.f. of a given number always divides its l.c.m.
9. Mensuration 2D and 3D
With the help of the mensuration formulas, you will be able to know and calculate the areas, perimeter, volume, total surface area, curved surface area, length, etc. of different geometrical figures. We have provided you with the formulas which are most expected to be used in your specific exam.
Check this out:
| Mensuration Formulas for 2-Dimensional Figures | ||
| Shape | Area | Perimeter |
| Circle | πr² | 2 π r |
| Square | (side)² | 4 × side |
| Rectangle | length × breadth | 2 (length + breadth) |
| Scalene Triangle | √[s(s−a)(s−b)(s−c), Where, s = (a+b+c)/2 |
a+b+c (sum of sides) |
| Isosceles Triangle | ½ × base × height | 2a + b (sum of sides) |
| Equilateral Triangle | (√3/4) × (side)² | 3 × side |
| Right Angled Triangle | ½ × base × hypotenuse | A + B + hypotenuse, where the hypotenuse is √A²+B² |
| Parallelogram | base × height | 2(l+b) |
| Rhombus | ½ × diagonal1 × diagonal2 | 4 × side |
| Trapezium | ½ h(sum of parallel sides) | a+b+c+d (sum of all sides) |
Mensuration Formulas for 3-Dimensional Figures
| Mensuration Formulas for 3-Dimensional Figures | |||
|---|---|---|---|
| Shape | Area | CSA/LSA | TSA |
| Cone | (1/3) π r² h | π r l | πr (r + l) |
| Cube | (side)³ | 4 (side)² | 6 (side)² |
| Cuboid | length × breadth × height | 2 height (length + breadth) | 2 (lb +bh +hl) |
| Cylinder | π r² h | 2π r h | 2πrh + 2πr² |
| Hemisphere | (2/3) π r³ | 2 π r² | 3 π r² |
| Sphere | 4/3πr³ | 4πr² | 4πr² |
10. Simple Interest and Compound Interest
Simple interest is based on the principal amount of a loan or deposit. In contrast, compound interest is based on the principal amount and the interest that accumulates on it in every period.
Simple Interest:
1) SI = P x R x T/100
2) Principal = Simple Interest ×100/ R × T
3) Rate of Interest = Simple Interest ×100 / P × T
4) Time = Simple Interest ×100 / P × R
5) If the rate of Simple interest differs from year to year, then
Simple Interest = Principal × (R1+R2+ R3…..)/100
The four variables in the above formula are: SI=Simple Interest P=Principal Amount (This the amount invested)T=Number of yearsR=Rate of interest (per year) in percentage
Compound Interest:
The difference between the amount and the money borrowed is called the compound interest for a given period of time
1) Let principal =P; time =n years; and rate = r% per annum and let A be the total amount at the end of n years, then
A = P*[1+ (r/100)]n;
CI = {P*[1+ (r/100)]n -1}
2) When compound interest reckoned half-yearly, then r% become r/2% and time n becomes 2n;
= P*[1+ (r/2*100)]2n
3) For the quarterly
A= P*[1+ (r/4*100)]4n
4) The difference between compound interest and simple interest over two years is given by
Pr2/1002or P(r/100)2
5) The difference between compound interest and simple interest over three years is given by
P(r/100)2*{(r/100)+3}
6) When Rates are different for different years, say R1%, R2%, R3% for 1st, 2nd and 3rd year respectively, Then the total amount is given by
P ((1 + R1)/100) ((1 + R2)/100) ((1 + R2)/100)
7) Present worth of Rs. x due n years hence is given by
x/(1+R/100)
11. Boat and Stream Formula
Downstream and Upstream: When considering water travel, the direction aligned with the stream is known as downstream, while the direction opposing the stream is referred to as upstream.
If the boat’s velocity in calm water is denoted as u km/hr, and the velocity of the stream is represented by v km/hr, then the following relationships hold:
- Speed downstream = (u + v) km/hr.
- Speed upstream = (u – v) km/hr.
In scenarios where the speed downstream is a km/hr and the speed upstream is b km/hr, the boat’s velocity in still water can be calculated as:
- Speed in still water = ½ (a + b) km/hr;
- Rate of the stream = ½ (a – b) km/hr.
Importance Of Maths Formulas
Mathematics is a subject heavily reliant on formulas, and this study material aids effective memorization. The provided time-syllabus dependent strategy guides students in progressing systematically. Efforts have been made to minimize the time constraints often faced by students during exam preparation.
- A comprehensive study of math formulas allows students to assess their strengths and weaknesses.
- Strengths can be maintained, while weaknesses can be addressed with focused efforts.
- Special attention is given to understand math formulas with detailed explanations for better understanding.
- Strategies are made by experienced subject experts assist students in effective preparation.
Maths Formulae PDF
Download the Mathematics Formuale PDF and know the most important formulae for the maths section, which will help you solve questions on time and find accurate answers. Solve as many questions as possible as this is the most important key to acing the maths section in a competitive exam.













