Surface Area of a Cone- Explanation, Formula, Derivation, Examples

Surface Area of a Cone: In geometry and solid geometry, the surface area of a cone is a fundamental concept. The concept of surface area comes in handy in many engineering and mathematical domains. The surface area of a cone is basically the area occupied by the surface of a cone. A cone is a three-dimensional shape that has a circle as a base. A cone is of tow types: a right circular cone (that is the cone is symmetrical in shape) and an oblique cone. We will focus our energy on the right circular cone in this article. A three-dimensional object’s surface area is the total of all of its sides’ surface areas. You all must have seen a cone in your day-to-day life. A birthday cap is a prime example of a conical shape. In this article, we will learn about the surface area of the cone and go through its different aspects including the derivation of its formula.

Surface Area of a Cone

A cone’s surface area means the area occupied the surfaces of a cone. A cone has a lateral surface and a circular base. That is why a cone has two types of surface area: Lateral Surface Area and Total Surface Area. The lateral surface area is also known as the curved surface area. A cone’s curved or lateral surface area mans the area occupied by its lateral or curved surface. The total surface area (sometimes simply called surface area) of a cone is the area occupied all its surfaces, i.e., the area occupied the lateral surface and the base. So we can say that the total surface area is equal to curved surface area + base area. Cone’s surface area is expressed in square units. Before exploring its surface area, let us get acquainted with its lengths.

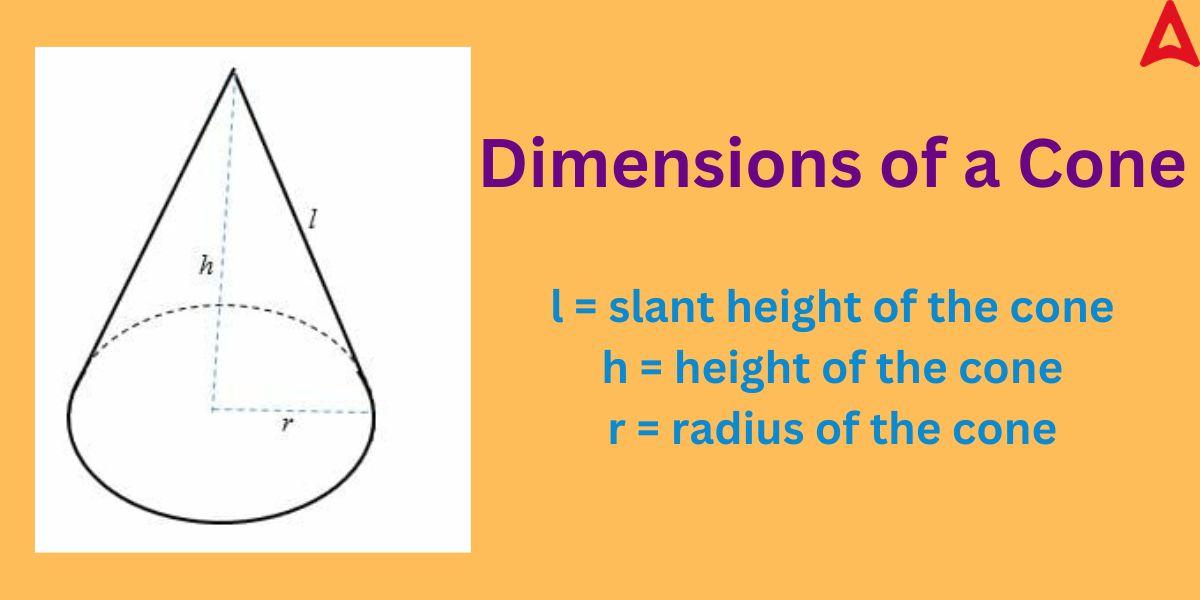
The height (h) of the cone is the length from the center of its circular base to the tip of the cone.

The distance from the vertex to the edge of the cone’s circular base is its slant height. It is denoted by “l”.

As the base of the cone is circular, so it has a radius denoted by “r”.

The above-mentioned lengths will become more clear to you by observing the diagram given below

Surface Area of a Cone Formula

The shape of a cone is produced by stacking several triangles and spinning them around an axis. It has a total surface area and a curved surface area because its base is flat. The formula of both these areas is given below. As stated above, the surface area implies total surface area, i.e., the total space occupied by the surfaces of a cone.

The surface area of a cone is given as:

Total Surface Area of a Cone: Π.r.(r + (√r² + h²))

where, r = radius of the cone

h = height of the cone

Curved/Lateral Surface Area of a Cone: Πrl

where, r = radius

l = slant height of the cone

Surface Area of a Cone with Slant Height

We can find out the surface area of a cone can be expressed in terms of slant height. The slant height is related to the radius and height h of the cone. The relation is given by:

l = √r² + h²

as, cone’s surface area is given by Π.r.(r + (√r² + h²))

on substituting √r² + h² with l, we get:

cone’s surface area = Πr(r + l)

so, we can say that surface area of cone = Π.r.(r + (√r² + h²))        OR       Πr(r + l)

Lateral Surface Area of a Cone

As we know that the lateral surface area (LSA) of a cone is the space occupied by the curved surface of a cone. It is analogous to the curved surface of your birthday cap. A cone’s lateral surface area is given by:

LSA = Πrl

where, Π = 22/7 or 3.14

r = radius of the cone’s circular base

l = slant height

Curved Surface Area of a Cone

A cone’s curved surface area (CSA) is equal to its lateral area. That is, the curved surface area is another name for the lateral surface area.

Hence, cone’s curved surface area = cone’s lateral surface area

So, CSA = Πrl

where, Π = 22/7 or 3.14

r = radius of the cone’s circular base

l = slant height

Surface Area of a Cone Derivation

We can derive the formula obtained above for the cone’s surface area. To do that, we have to understand the geometry of a cone. Let us derive its formula by referencing the figure given below:

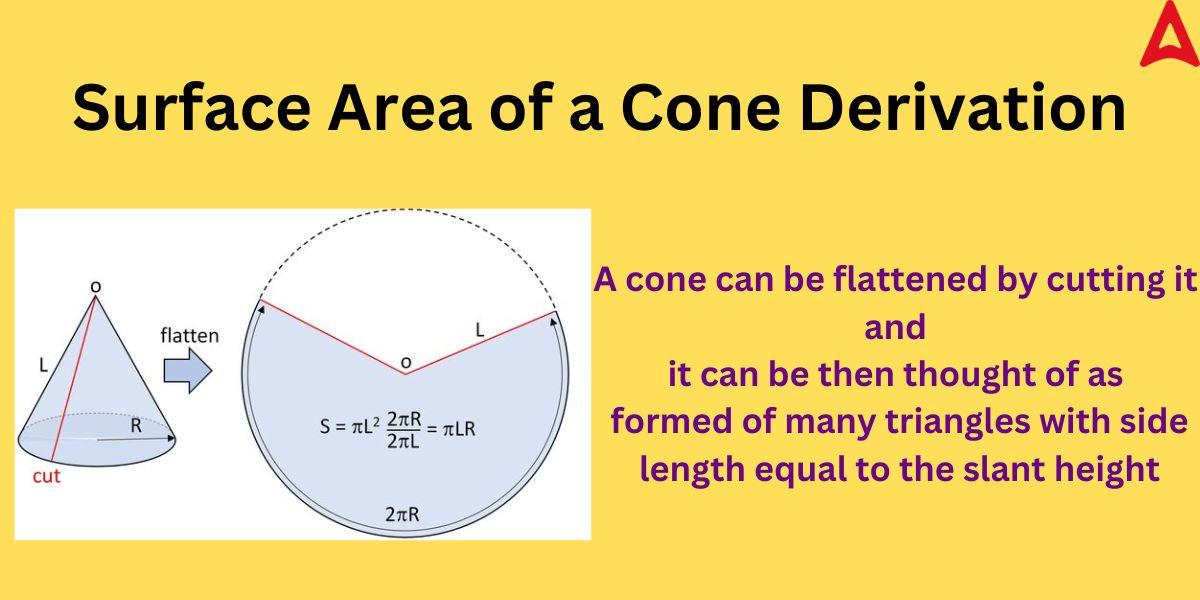
As shown above, a cone can be thought of as made up of many small triangles with arm length equal to “l”. Let the cone be cut and flattened into many small triangles A1, A2, A3, ………An. As is is the curved surface that is cut and flattened, so the total area of all these triangles will be equal to the curved surface area.

Hence, Curved surface area (CSA) of the cone = area of (A1 + A2 + A3 + ……..An)

as area of a triangle with base b and heigh h is given by (1/2) x b x h

so, CSA of the cone = [(1/2) x b1 x h1 + (1/2) x b2 x h2 + (1/2) x b3 x h3 + ……….+ (1/2) x bn x hn)]

as height of the individual triangle will be equal to the slant height of the cone

Hence, [(1/2) x b1 x l + (1/2) x b2 x l + (1/2) x b3 x l + ……….+ (1/2) x bn x l)]

Taking out (1/2) x l common, we get

(1/2) x l (b1 + b2 + b3+………. + bn)

as b1 + b2 + b3+………. + bn = total length of the base = circumference of the circle at the base of the cone

so, circumference = 2Πr, where r = radius of the cone

putting this in place of b1 + b2 + b3+………. + bn, we get

(1/2) x l x 2Πr

Hence, CSA of the cone = Πrl

As we know surface area (Total surface area) of the cone = curved surface area + area of the base

as the base of a cone is circle, so area will be given by Πr²

So, cone’s surface area = Πrl + Πr²

or, cone’s surface area = Πr (r + l) = Πr (r + √r² + h²)    (because l = √r² + h²)

Surface Area of Cone Formula Class 9

The surface area of a cone is one of the most important topics in class 9 solid geometry syllabus. There are some basic formulas for class 9 students, related to this topic, that they should memorize. The formulas are mentioned below.

• Curved/Lateral Surface area of the cone = Πrl
• Cone’s total surface area with slant height= Πr (r + l)
• Total surface area of a right circular cone without slant height = Πr (r + √r² + h²)
• slant height l = √r² + h²
• circumference of the base of a cone = 2Πr
• base area of the cone = Πr²

Surface Area of a Cone Examples

Below, we have mentioned some of the solved questions on cone’s surface area topic. These solved examples will give students a boost in their preparation. Students will be able to apply this concept after going the the examples given below.

Example 1: Determine the surface area of a cone with a 10 cm radius and a 20 cm slant height. Take the value of Π as 3.14.

Solution: As we have been asked the cone’s surface area, i.e., total surface area of the cone.

we know, cone’s total surface area = Πr (r + l)

given r = 10 cm

l = 20 cm

substituting these values in the formula

TSA = 3.14 x 10 (10 + 20)

TSA = 31.4 x 30

Hence, cone’s total surface area = 942 cm²

Example 2: A cone has a 7 cm radius and a surface area of 968 cm². Determine the cone’s slant height. Take Π = 22/7.

Solution: given, radius (r) of the cone = 7 cm

cone’s surface area = 968 cm²

as cone’s surface area = Πr (r + l)

968 = (22/7) x 7 (7 + l)

968/22 = 7 + l

l + 7 = 44

l = 44-7

l = 37

Hence, slant height of the cone = 37 cm

Example 3: Given the height of the cone to be 3 cm and the radius of its base 4 cm. What will be the surface area of this cone? Take the value of Π as 3.14.

Solution: Given , r = 4 cm

h = 3 cm

as a cone’s surface area in terms of height = Πr (r + √r² + h²)

substituting the values in the formula, we get

3.14 x 4 x (4 + √4² + 3²)

12.56 (4 + √25)

surface area of the cone = 12.56 x 9

hence, surface area = 113.04 cm²

Example 4: A cone whose base radius is given to be 9 cm has 14 cm slant height. What will be the curved surface area of this cone? Take Π = 22/7.

Solution: as we know, curved surface area of a right circular cone = Πrl

given, base radius (r) = 9 cm

slant height (l) = 14 cm

substituting these values in the cone’s curved surface area formula, we get

(22/7) x 9 x 14

396

Hence, curved surface area of this cone = 396 cm²

Example 5: What will be the radius of a cone whose curved surface area is 616 cm² and its slant height is 10 cm. Take the value of Π as 22/7.

Solution: given the curved surface area of a cone = 616 cm²

slant height (l) = 10 cm

As we know, cone’s curved surface = Πrl

so, 616 = (22/7) x r x 10

=> 616 x(7/22) = r x 10

=> r x 10 = 196

=> r = 196/10

r = 19.6

Hence, the radius of the cone = 19.6 cm

Sharing is caring!