The JEE Advanced 2024 exam has been successfully administered by the conducting authorities. This year’s exam was conducted by IIT Madras. Students can check the JEE Advanced question paper 2024 on this page that students had to solve on the IIT JEE examination day.
The Joint Entrance Exam (JEE) Advanced exam’s question paper consists of questions from class 11th and class 12th curriculum. The paper contains questions from Physics, Mathematics, and Chemistry subjects. The JEE Advanced exam 2024 was held on May 26 is held for admission to engineering, architecture, and other programs in IITs.
JEE Advanced Question Paper 2024
The JEE Advanced 2024 exam has two question papers: paper 1 and Paper 2. The Paper 1 exam was held in the morning shift from 9 AM to 12 noon while the Paper 2 exam was conducted in the afternoon session from 2:30 PM to 5:30 PM. The JEE Advanced question paper comes in two languages: Hindi and English. Along with the question paper, students can also check the exam analysis for the paper 1 and paper 2.
JEE Advanced 2024 Question Paper Highlights
The JEE Advanced 2024 exam was organized in online mode, i.e., the test was administered on a computer.
| Particulars | Details |
| Exam Name | JEE Advanced Exam 2024 |
| Administered by | IIT Madras |
| Exam Level | National Level Exam |
| Exam Date | May 26, 2024 |
| Number of Question papers in Exam | Two (Paper 1 & Paper 2) |
| JEE Advanced Paper 1 Exam Time | 9 AM to 12 PM |
| JEE Advanced Paper 2 Exam Time | 2:30 PM to 5:30 PM |
| Exam Mode | CBT (Computer Based Test) |
| Question Paper Medium | English and Hindi |
IIT JEE Exam Question Paper 2024
The JEE Advanced exam was previously known by the name IIT JEE Exam. The JEE Advanced paper 1 and paper consisted of 51 questions each. As the question paper has 3 sections, there was 17 questions each from the physics, chemistry and maths section in both paper 1 and paper 2. IIT Madras has published the official question papers on the JEE Advanced website, jeeadv.ac.in.
JEE Advanced Question Paper PDF 2024
Checkout the official Paper 1 and Paper 2 PDF for the JEE Advanced 2024 exam in both Hindi and English medium below.
JEE Advanced 2024 Paper 1 (Hindi Medium)
JEE Advanced 2024 Paper 1 (English Medium)
JEE Advanced 2024 Paper 2 (Hindi Medium)
JEE Advanced 2024 Paper 2 (English Medium)
IIT JEE Question Paper 2024 Analysis
The analysis of the JEE(Advanced) 2024 question paper is provided below on the basis of the student’s experience with the exam paper. Exam analysis for JEE Advanced 2024 paper 1 and paper 2 may be seen here.
JEE Advanced 2024 Paper 1 Analysis: Paper 1 consists of 51 questions, with 17 questions in mathematics, 17 in physics, and 17 in chemistry. There was 180 marks available overall, with a moderate level of difficulty. The Physics section was moderate to difficult, chemistry was moderately difficult, and mathematics was regarded as the most difficult.
JEE Advanced 2024 Paper 2 Analysis: Compared to Paper 1, Paper 2 had a harder difficulty level. Paper 2 consisted of 51 questions, with 17 questions in each of the subjects of mathematics, physics, and chemistry. There were 180 marks available in total. Physics was easy to moderately challenging, chemistry was quite difficult, and mathematics was exceptionally tough.
JEE Advanced Expected Question paper 2024
The best way to solve any question in the might JEE Advanced exam is to solve the expected questions that have been made by experts. These questions features exactly the same questions which can be asked in the exam on May 26. Take a look at the Paper 1 and Paper 2 sample questions and solve them to increase your marks and rank.
Physics Questions
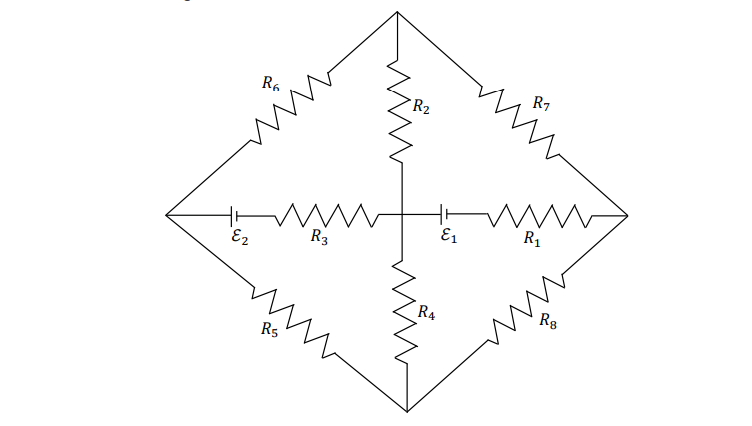
Q 1) The figure shows a circuit having eight resistances of 1 Ω each, labelled 𝑅1 to 𝑅8, and two ideal
batteries with voltages ℰ = 12 𝑉 and ℰ = 6.
Q 2) The smallest division on the main scale of a Vernier calipers is 0.1 cm. Ten divisions of the Vernier scale correspond to nine divisions of the main scale. The figure below on the left shows the reading of this calipers with no gap between its two jaws. The figure on the right shows the reading with a solid sphere held between the jaws. The correct diameter of the sphere is
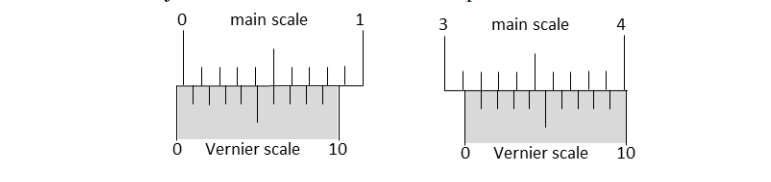
(A) 3.07 cm (B) 3.11 cm (C) 3.15 cm (D) 3.17 cm
Q 3) An ideal gas undergoes a four step cycle as shown in the 𝑃 − 𝑉 diagram below.
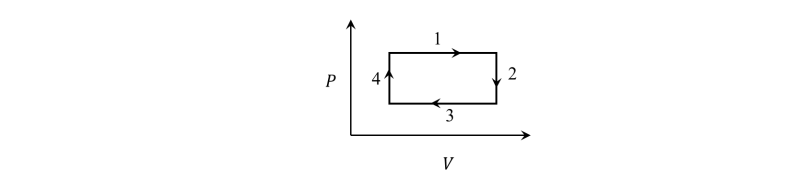
During this cycle, heat is absorbed by the gas in
(A) steps 1 and 2 (B) steps 1 and 3
(C) steps 1 and 4 (D) steps 2 and 4
Q 4) An extended object is placed at point O, 10 cm in front of a convex lens L1 and a concave lens L2 is placed 10 cm behind it, as shown in the figure. The radii of curvature of all the curved surfaces in both the lenses are 20 cm. The refractive index of both the lenses is 1.5. The total magnification of this lens system is
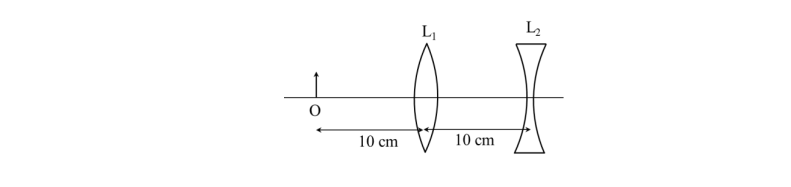
(A) 0.4 (B) 0.8 (C) 1.3 (D) 1.6
Q 5) A heavy nucleus Q of half-life 20 minutes undergoes alpha-decay with probability of 60% and beta-decay with probability of 40%. Initially, the number of Q nuclei is 1000. The number of alpha-decays of Q in the first one hour is
(A) 50 (B) 75 (C) 350 (D) 525
Question Stem for Question Nos. 6 and 7
Question Stem
A projectile is thrown from a point O on the ground at an angle 45° from the vertical and with a speed 5√2 m/s. The projectile at the highest point of its trajectory splits into two equal parts. One part falls vertically down to the ground, 0.5 s after the splitting. The other part, 𝑡 seconds after the splitting, falls to the ground at a distance 𝑥 meters from the point O. The acceleration due to gravity 𝑔 = 10 m/s².
Q.6 The value of 𝑡 is ___ .
Q.7 The value of 𝑥 is ___ .
Question Stem for Question Nos. 8 and 9
Question Stem
In the circuit shown below, the switch S is connected to position P for a long time so that the charge on the capacitor becomes 𝑞1 µC. Then S is switched to position Q. After a long time, the charge on the capacitor is 𝑞2 µC.
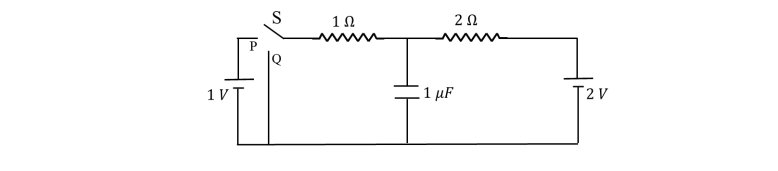
Q.8 The magnitude of 𝑞1 is ___ .
Q.9 The magnitude of 𝑞2 is ___ .
Q 10) An 𝛼-particle (mass 4 amu) and a singly charged sulfur ion (mass 32 amu) are initially at rest. They are accelerated through a potential V and then allowed to pass into a region of uniform magnetic field which is normal to the velocities of the particles. Within this region, the 𝛼-particle and the sulfur ion move in circular orbits of radii 𝑟𝛼 and 𝑟𝑆, respectively. The ratio (𝑟𝑆/𝑟𝛼) is ___.
Q 11) A small object is placed at the center of a large evacuated hollow spherical container. Assume that the container is maintained at 0 K. At time 𝑡 = 0, the temperature of the object is 200 K. The temperature of the object becomes 100 K at 𝑡 = 𝑡1 and 50 K at 𝑡 = 𝑡2. Assume the object and the container to be ideal black
bodies. The heat capacity of the object does not depend on temperature. The ratio (𝑡2/𝑡1) is ___.
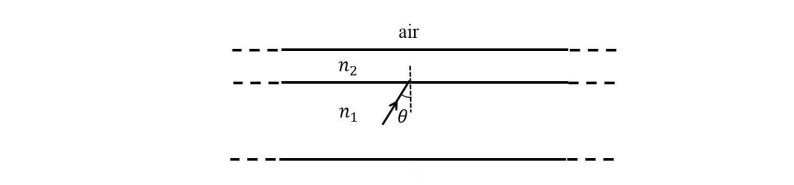
Q 12) A wide slab consisting of two media of refractive indices 𝑛1 and 𝑛2 is placed in air as
shown in the figure. A ray of light is incident from medium 𝑛1 to 𝑛2 at an angle 𝜃, where sin 𝜃 is slightly larger than 1/𝑛1. Take refractive index of air as 1. Which of the following statement(s) is(are) correct?
Q 13) Put a uniform meter scale horizontally on your extended index fingers with the left one at 0.00 cm
and the right one at 90.00 cm. When you attempt to move both the fingers slowly towards the center,
initially only the left finger slips with respect to the scale and the right finger does not. After some
distance, the left finger stops and the right one starts slipping. Then the right finger stops at a distance
𝑥𝑅 from the center (50.00 cm) of the scale and the left one starts slipping again. This happens
because of the difference in the frictional forces on the two fingers. If the coefficients of static and
dynamic friction between the fingers and the scale are 0.40 and 0.32, respectively, the value of 𝑥𝑅 (in
cm) is ______.
Q 14) When water is filled carefully in a glass, one can fill it to a height h above the rim of the glass due to
the surface tension of water. To calculate h just before water starts flowing, model the shape of the
water above the rim as a disc of thickness h having semicircular edges, as shown schematically in the
figure. When the pressure of water at the bottom of this disc exceeds what can be withstood due to
the surface tension, the water surface breaks near the rim and water starts flowing from there. If the
density of water, its surface tension and the acceleration due to gravity are 103kg m−3, 0.07 Nm−1
and 10 ms−2, respectively, the value of h (in mm) is _________.
Q 15) A source, approaching with speed 𝑢 towards the open end of a stationary pipe of length 𝐿, is emitting a sound of frequency 𝑓𝑠. The farther end of the pipe is closed. The speed of sound in air is 𝑣 and 𝑓0 is the fundamental frequency of the pipe. For which of the following combination(s) of 𝑢 and 𝑓𝑠 , will the sound reaching the pipe lead to a resonance?
(A) 𝑢 = 0.8𝑣 and 𝑓𝑠 = 𝑓0
(B) 𝑢 = 0.8𝑣 and 𝑓𝑠 = 2𝑓0
(C) 𝑢 = 0.8𝑣 and 𝑓𝑠 = 0.5𝑓0
(D) 𝑢 = 0.5𝑣 and 𝑓𝑠 = 1.5𝑓0
Question Stem
A pendulum consists of a bob of mass 𝑚 = 0.1 kg and a massless inextensible string of length 𝐿 = 1.0 m. It is suspended from a fixed point at height 𝐻 = 0.9 m above a frictionless horizontal floor. Initially, the bob of the pendulum is lying on the floor at rest vertically below the point of suspension. A horizontal impulse 𝑃 = 0.2 kg-m/s is imparted to the bob at some instant. After the bob slides for some distance, the string becomes taut and the bob lifts off the floor. The magnitude of the angular momentum of the pendulum about the point of suspension just before the bob lifts off is 𝐽 kg-m2 /s. The kinetic energy of the pendulum just after the liftoff is 𝐾 Joules.
Q 16) The value of 𝐽 is ___ .
Q 17) The value of 𝐾 is ___.
Question Stem
In a circuit, a metal filament lamp is connected in series with a capacitor of capacitance C 𝜇𝐹 across a 200 V, 50 Hz supply. The power consumed by the lamp is 500 W while the voltage drop across it is 100 V. Assume that there is no inductive load in the circuit. Take rms values of the voltages. The magnitude of the phaseangle (in degrees) between the current and the supply voltage is 𝜑. Assume, 𝜋√3 ≈ 5.
Q 18) The value of C is ___.
Q 19) The value of 𝜑 is ___.
Q 20) The distance between two stars of masses 3𝑀𝑆 and 6𝑀𝑆 is 9𝑅. Here 𝑅 is the mean distance between the centers of the Earth and the Sun, and 𝑀𝑆 is the mass of the Sun. The two stars orbit around their common center of mass in circular orbits with period 𝑛𝑇, where 𝑇 is the period of Earth’s revolution around the Sun. The value of n is ___.
Chemistry Section Questions
Q 1) An acidified solution of 0.05 M Zn2+ is saturated with 0.1 M H2S. What is the minimum molar
concentration (M) of H+ required to prevent the precipitation of ZnS? Use 𝐾sp (ZnS) = 1.25 × 10−22 and
overall dissociation constant of H2S, 𝐾NET = 𝐾1𝐾2 = 1 × 10−21.
Q 2) Consider the reaction sequence from P to Q shown below. The overall yield of the major product Q
from P is 75%. What is the amount in grams of Q obtained from 9.3 mL of P? (Use density of P =
1.00 g mL−1; Molar mass of C = 12.0, H =1.0, O =16.0 and N = 14.0 g mol−1)

Q 3) Liquids A and B form ideal solution for all compositions of A and B at 25 ℃. Two such solutions
with 0.25 and 0.50 mole fractions of A have the total vapor pressures of 0.3 and 0.4 bar, respectively.
What is the vapor pressure of pure liquid B in bar?
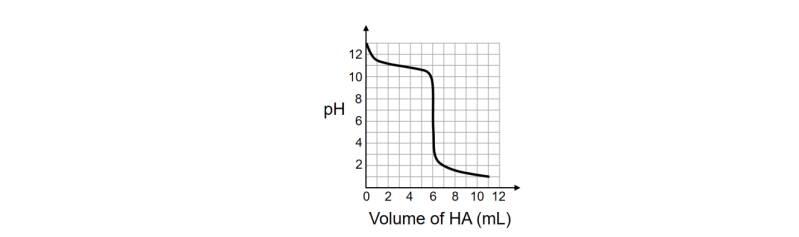
Q 4) A solution of 0.1 M weak base (B) is titrated with 0.1 M of a strong acid (HA). The variation of pH
of the solution with the volume of HA added is shown in the figure below. What is the p𝐾b of the
base? The neutralization reaction is given by B + HA → BH+ + A− .
Q 5) Choose the correct statement(s) among the following.
(A) SnCl2.2H2O is a reducing agent.
(B) SnO2 reacts with KOH to form K2[Sn(OH)6].
(C) A solution of PbCl2 in HCl contains Pb2+and Cl−ions.
(D) The reaction of Pb3O4 with hot dilute nitric acid to give PbO2 is a redox reaction.
Q 6) Which among the following statement(s) is(are) true for the extraction of aluminium from bauxite?
(A) Hydrated Al2O3 precipitates, when CO2 is bubbled through a solution of sodium aluminate.
(B) Addition of Na3AlF6 lowers the melting point of alumina.
(C) CO2 is evolved at the anode during electrolysis.
(D) The cathode is a steel vessel with a lining of carbon.
Q 7) An organic compound (C8H10O2) rotates plane-polarized light. It produces pink color with neutral
FeCl3 solution. What is the total number of all the possible isomers for this compound?
Q 8) In the chemical reaction between stoichiometric quantities of KMnO4 and KI in weakly basic solution, what is the number of moles of I2 released for 4 moles of KMnO4 consumed?
Q 9) An acidified solution of potassium chromate was layered with an equal volume of amyl alcohol.
When it was shaken after the addition of 1 mL of 3% H2O2, a blue alcohol layer was obtained. The
blue color is due to the formation of a chromium (VI) compound ‘X’. What is the number of oxygen
atoms bonded to chromium through only single bonds in a molecule of X?
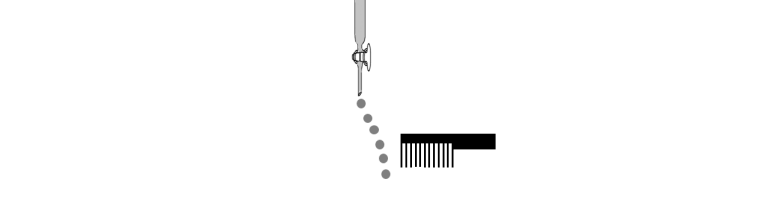
Q 10) Consider the following compounds in the liquid form:
O2, HF, H2O, NH3, H2O2, CCl4, CHCl3, C6H6, C6H5Cl.
When a charged comb is brought near their flowing stream, how many of them show deflection as per the following figure?
Q 11) The calculated spin only magnetic moments of [Cr(NH3)6]3+ and [CuF6]3– in BM, respectively, are
(Atomic numbers of Cr and Cu are 24 and 29, respectively)
(A) 3.87 and 2.84 (B) 4.90 and 1.73
(C) 3.87 and 1.73 (D) 4.90 and 2.84
Q 12) The correct statement(s) related to colloids is(are)
(A) The process of precipitating colloidal sol by an electrolyte is called peptization.
(B) Colloidal solution freezes at higher temperature than the true solution at the same concentration.
(C) Surfactants form micelle above critical micelle concentration (CMC). CMC depends on temperature.
(D) Micelles are macromolecular colloids
Q 13) The correct statement(s) related to the metal extraction processes is(are)
(A) A mixture of PbS and PbO undergoes self-reduction to produce Pb and SO2.
(B) In the extraction process of copper from copper pyrites, silica is added to produce copper silicate.
(C) Partial oxidation of sulphide ore of copper by roasting, followed by self-reduction produces blister copper.
(D) In cyanide process, zinc powder is utilized to precipitate gold from Na[Au(CN)2].
Q 14) The maximum number of possible isomers (including stereoisomers) which may be formed on mono-bromination of 1-methylcyclohex-1-ene using Br2 and UV light is ___.
Q 15) The total number of possible isomers for [Pt(NH3)4Cl2]Br2 is ___.
Q 16) The correct statement(s) related to oxoacids of phosphorous is(are)
(A) Upon heating, H3PO3 undergoes disproportionation reaction to produce H3PO4 and PH3.
(B) While H3PO3 can act as reducing agent, H3PO4 cannot.
(C) H3PO3 is a monobasic acid.
(D) The H atom of P–H bond in H3PO3 is not ionizable in water.
Q 17) The pair(s) of complexes wherein both exhibit tetrahedral geometry is(are)
(Note: py = pyridine
Given: Atomic numbers of Fe, Co, Ni and Cu are 26, 27, 28 and 29, respectively)
(A) [FeCl4]– and [Fe(CO)4]2–
(B) [Co(CO)4]– and [CoCl4]2–
(C) [Ni(CO)4] and [Ni(CN)4]2–
(D) [Cu(py)4]+ and [Cu(CN)4]3–
Q 18) Ozonolysis of ClO2 produces an oxide of chlorine. The average oxidation state of chlorine in this oxide is ___.
Q 19) Consider a helium (He) atom that absorbs a photon of wavelength 330 nm. The change in the velocity (in cm s–1) of He atom after the photon absorption is ___.
(Assume: Momentum is conserved when photon is absorbed.
Use: Planck constant = 6.6 ×10–34 J s, Avogadro number = 6 ×1023 mol–1, Molar mass of He = 4 g mol–1)
A 20) The treatment of galena with HNO3 produces a gas that is
(A) paramagnetic (B) bent in geometry
(C) an acidic oxide (D) colorless
JEE Advanced Mathematics Questions 2024
Q 1) The probability that a missile hits a target successfully is 0.75. In order to destroy the target
completely, at least three successful hits are required. Then the minimum number of missiles that
have to be fired so that the probability of completely destroying the target is NOT less than 0.95, is
_____
Q 2) The trace of a square matrix is defined to be the sum of its diagonal entries. If 𝐴 is a 2 × 2 matrix
such that the trace of 𝐴 is 3 and the trace of 𝐴³ is −18, then the value of the determinant of 𝐴 is _____
Q 3) Let 𝛼, 𝛽, 𝛾, 𝛿 be real numbers such that 𝛼² + 𝛽² + 𝛾² ≠ 0 and 𝛼 + 𝛾 = 1. Suppose the point
(3, 2, −1) is the mirror image of the point (1, 0, −1) with respect to the plane 𝛼𝑥 + 𝛽𝑦 + 𝛾𝑧 = 𝛿. Then which of the following statements is/are TRUE?
(A) 𝛼 + 𝛽 = 2 (B) 𝛿 − 𝛾 = 3
(C) 𝛿 + 𝛽 = 4 (D) 𝛼 + 𝛽 + 𝛾 = 𝛿
Q 4) An engineer is required to visit a factory for exactly four days during the first 15 days of every
month and it is mandatory that no two visits take place on consecutive days. Then the number of all
possible ways in which such visits to the factory can be made by the engineer during 1-15 June
2021 is _____
Q 5) In a hotel, four rooms are available. Six persons are to be accommodated in these four rooms in
such a way that each of these rooms contains at least one person and at most two persons. Then the
number of all possible ways in which this can be done is _____
Q 6) Two fair dice, each with faces numbered 1, 2, 3, 4, 5 and 6, are rolled together and the sum of the
numbers on the faces is observed. This process is repeated till the sum is either a prime number or a
perfect square. Suppose the sum turns out to be a perfect square before it turns out to be a prime
number. If 𝑝 is the probability that this perfect square is an odd number, then the value of 14𝑝 is
_____
Q 7) Let 𝐶1 and 𝐶2 be two biased coins such that the probabilities of getting head in a single toss are 2/3 and 1/3, respectively. Suppose 𝛼 is the number of heads that appear when 𝐶1 is tossed twice, independently, and suppose 𝛽 is the number of heads that appear when 𝐶2 is tossed twice, independently. Then the probability that the roots of the quadratic polynomial 𝑥² − 𝛼𝑥 + 𝛽 are real and equal, is
(A) 40/81
(B) 20/81
(C) 1/2
(D) 1/4
Q 8) Consider all rectangles lying in the region
{(𝑥, 𝑦) ∈ ℝ × ℝ ∶ 0 ≤ 𝑥 ≤𝜋/2 and 0 ≤ 𝑦 ≤ 2 sin(2𝑥)}
and having one side on the 𝑥-axis. The area of the rectangle which has the maximum perimeter
among all such rectangles, is
(A)3𝜋/2
(B) 𝜋
(C) 𝜋/2√3
(D) 𝜋√3/2
Q 9) Let the function 𝑓: ℝ → ℝ be defined by 𝑓(𝑥) = 𝑥³ − 𝑥² + (𝑥 − 1) sin 𝑥 and let 𝑔: ℝ → ℝ be an arbitrary function. Let 𝑓𝑔: ℝ → ℝ be the product function defined by (𝑓𝑔)(𝑥) = 𝑓(𝑥)𝑔(𝑥). Then which of the following statements is/are TRUE?
(A) If 𝑔 is continuous at 𝑥 = 1, then 𝑓𝑔 is differentiable at 𝑥 = 1
(B) If 𝑓𝑔 is differentiable at 𝑥 = 1, then 𝑔 is continuous at 𝑥 = 1
(C) If 𝑔 is differentiable at 𝑥 = 1, then 𝑓𝑔 is differentiable at 𝑥 = 1
(D) If 𝑓𝑔 is differentiable at 𝑥 = 1, then 𝑔 is differentiable at 𝑥 = 1
Q 10) Let 𝑎1, 𝑎2, 𝑎3, … be a sequence of positive integers in arithmetic progression with common difference 2. Also, let 𝑏1, 𝑏2, 𝑏3, … be a sequence of positive integers in geometric progression with common ratio 2. If 𝑎1 = 𝑏1 = 𝑐, then the number of all possible values of 𝑐, for which the equality
2(𝑎1 + 𝑎2 + ⋯ + 𝑎𝑛) = 𝑏1 + 𝑏2 + ⋯ + 𝑏𝑛
holds for some positive integer 𝑛, is _____
Q 11) Consider a triangle ∆ whose two sides lie on the x-axis and the line 𝑥 + 𝑦 + 1 = 0. If the orthocenter of ∆ is (1, 1), then the equation of the circle passing through the vertices of the triangle ∆ is
(A) 𝑥² + 𝑦² − 3𝑥 + 𝑦 = 0
(B) 𝑥² + 𝑦² + 𝑥 + 3𝑦 = 0
(C) 𝑥² + 𝑦² + 2𝑦 − 1 = 0
(D) 𝑥² + 𝑦² + 𝑥 + 𝑦 = 0
Q 12) Three numbers are chosen at random, one after another with replacement, from the set 𝑆 = {1,2,3, …,100}. Let 𝑝1 be the probability that the maximum of chosen numbers is at least 81 and 𝑝2 be the probability that the minimum of chosen numbers is at most 40. The value of 625/4 𝑝1 is ___ .
Q 13) For 𝑥 ∈ ℝ, the number of real roots of the equation
3𝑥² − 4|𝑥² − 1| + 𝑥 − 1 = 0 is ___ .
Q 14) Let 𝐸 denote the parabola 𝑦² = 8𝑥. Let 𝑃 = (−2, 4), and let 𝑄 and 𝑄′ be two distinct points on 𝐸 such that the lines 𝑃𝑄 and 𝑃𝑄′ are tangents to 𝐸. Let 𝐹 be the focus of 𝐸. Then which of the following statements is (are) TRUE ?
(A) The triangle 𝑃𝐹𝑄 is a right-angled triangle
(B) The triangle 𝑄𝑃𝑄′ is a right-angled triangle
(C) The distance between 𝑃 and 𝐹 is 5√2
(D) 𝐹 lies on the line joining 𝑄 and 𝑄′
Q 15) In a study about a pandemic, data of 900 persons was collected. It was found that
190 persons had symptom of fever,
220 persons had symptom of cough,
220 persons had symptom of breathing problem,
330 persons had symptom of fever or cough or both,
350 persons had symptom of cough or breathing problem or both,
340 persons had symptom of fever or breathing problem or both,
30 persons had all three symptoms (fever, cough and breathing problem).
If a person is chosen randomly from these 900 persons, then the probability that the person has at most one symptom is _____________.
Q 16) Let 𝑀 be a 3 × 3 invertible matrix with real entries and let 𝐼 denote the 3 × 3 identity matrix. If
𝑀−1 = adj (adj 𝑀), then which of the following statements is/are ALWAYS TRUE?
(A) 𝑀 = 𝐼 (B) det 𝑀 = 1 (C) 𝑀² = 𝐼 (D) (adj 𝑀)² = I
Q 17) Which of the following statements is TRUE ?
(A) 𝑓(√ln 3) + 𝑔(√ln 3) =1/3
(B) For every 𝑥 > 1, there exists an 𝛼 ∈ (1, 𝑥) such that 𝜓1(𝑥) = 1 + 𝛼𝑥
(C) For every 𝑥 > 0, there exists a 𝛽 ∈ (0, 𝑥) such that 𝜓2(𝑥) = 2𝑥(𝜓1(𝛽) − 1)
(D) 𝑓 is an increasing function on the interval [0,3/2]
Q 18) Consider the parabola 𝑦² = 4𝑥. Let 𝑆 be the focus of the parabola. A pair of tangents drawn to the
parabola from the point 𝑃 = (−2, 1) meet the parabola at 𝑃1 and 𝑃2. Let 𝑄1 and 𝑄2 be points on the
lines 𝑆𝑃1 and 𝑆𝑃2 respectively such that 𝑃𝑄1 is perpendicular to 𝑆𝑃1 and 𝑃𝑄2 is perpendicular to
𝑆𝑃2. Then, which of the following is/are TRUE ?
(A) 𝑆𝑄1 = 2
(B) 𝑄1𝑄2 = 3√10/5
(C) 𝑃𝑄1 = 3
(D) 𝑆𝑄2 = 1
Q 19) Consider an experiment of tossing a coin repeatedly until the outcomes of two consecutive tosses
are same. If the probability of a random toss resulting in head is1/3, then the probability that the experiment stops with head is
(A) 1/3
(B) 5/21
(C) 4/21
(D) 2/7
Q 20) Let A1 ,A2,A3,…, A8 be the vertices of a regular octagon that lie on a circle of radius 2. Let P be a point on the circle and let PAi denote the distance between the points P and Ai for i = 1,2,…,8. If P varies over the circle, then the maximum value of the product PA1 . PA2 . ….. PA8, is
Tips to Score Better in JEE Advanced Exam 2024
The JEE Advanced exam will be taken by the top 2.5 lakh candidates who passed the JEE Main 2024 exam, leading to a cut throat competition. According to reports, the majority of the aspirants are from Telangana, Maharashtra, and Uttar Pradesh. Experts advise students to adhere to the following advice in order to maximize their performance on the engineering entrance exam:
- Get familiar with high-priority subjects and thoroughly prepare the chapters that were heavily weighted and frequently questioned in previous exam years.
- Develop a solid conceptual grasp of the underlying ideas, reasoning, and applications of concepts. This will help you to effectively answer a variety of inquiries.
- Create a plan for handling your time during the test. Sort the easy questions in order of priority to get the most marks in the allocated time and still have time for review.
- Prior to exam days, make sure you get enough sleep, drink enough of water, and eat a healthy diet.
- Have faith in your abilities to succeed and keep an optimistic outlook.













 JoSAA 2025 Mock Seat Allotment Round 1 R...
JoSAA 2025 Mock Seat Allotment Round 1 R...
 JAC Delhi Seat Allotment Result 2025 @ja...
JAC Delhi Seat Allotment Result 2025 @ja...
 JEE Advanced Toppers List 2025 OUT, Chec...
JEE Advanced Toppers List 2025 OUT, Chec...









