What is the difference between 2D and 3D shapes?

2D shapes are those geometric shapes that have only two dimensions. These two dimensions are known as length and breadth (also known as width). While 3D shapes are those shapes that have 3 dimensions, including length, breadth (width), and height (also known as depth or thickness).

Give some examples of 2D and 3D geometry shapes.

Some examples of 2D and 3D geometry shapes are given below: 2D shapes - square, rectangle, triangle, rhombus, parallelogram, etc. 3D shapes - cone, cube, cuboid, cylinder, etc

What is the formula to find the area of a rectangle?

The area of the rectangle is given by length x breadth

Geometry Formulas- Perimeter, Area, Volume, Examples -

Table of Contents

Geometry formulas are used to find the dimensions and related properties like perimeter, area, and volume of geometrical shapes. These formulas are used extensively in different fields of science and technology. Observing the importance of the formulas of Geometry, it is taught to students from the early years of their school. In this article, we will cover all the formulas of 2D and 3D geometry along with basic geometry formulas for some basic shapes like triangles, squares, rectangles, etc. These formulas will not only be useful for students of class 10 and class 12 who will be taking board exams shortly but will also help aspirants prepare for competitive exams.

Geometry Formulas

The geometry formulas are used to find out different attributes of a geometrical shape. These attributes can be dimensions like length, breadth, or height (in case of 3D shapes), areas, perimeters, and volumes (in case of 3D geometrical figures). In mathematics, geometry is the study of relationships between points, lines, angles, surfaces, measurements of solids, and their properties. The branch of Geometry can be broadly classified into two categories: 2D Geometry (two dimensional geometry) and 3D Geometry (three dimensional geometry).

In 2D geometry, we study about the 2D shapes, i.e., two dimensional shapes. These geometrical figures have only two dimensions- length and breadth (width). So, we can only find the area and perimeter of these shapes but their volume cannot be determined because of the absence of the third dimension. Some examples of 2D geometrical figures are triangle, square, circle, rectangle, etc.

3D geometry deals with the study of three dimensional geometrical figures. These geometrical shapes have three dimensions – length, breadth (width), and height (also called depth or thickness). Due to the presence of the third dimension, we can compute the volume of 3D shapes using the geometry formulas apart from finding the area and perimeter. Some examples of 3D geometrical figures are cone, sphere, cylinder, cube, etc.

Geometry Formulas for Beginners

Looking at the significance of the geometrical formula in the real world calculations and architecture, students are taught these formulas from high school itself. Students from class 8th to class 10th study different geometrical formulas to calculate areas and volumes of 2D and 3D shapes. Some of the important geometrical formulas for the beginner students are given below.

Area Formula

Area of Trapezium = height × (sum of parallel sides)/2
Area of Rhombus = (1/2) × d1 × d2; where d1 and d2 are the two diagonals of the rhombus
Area of Special Quadrilateral = (1/2) × d × (h1 + h2); where d is the diagonal, and h1 and h2 are the perpendiculars drawn on the diagonals from the vertices.
Surface area of Cuboid = 2(lb + bh + hl); where l, b and h represent the length, breadth and height of the cuboid.
Surface area of Cube = 6s²; where s represents the side of the cube.
Surface area of cylinder = 2Πr(r + h); where h represents the height and r represents the radius of the cylinder.
Area of an equilateral triangle = s²(√3/4), where s = side of the equilateral triangle
Area of a regular hexagon = (3 x √3 x a²)/2, where a = side of the regular hexagon

Volume Formula

Volume of Cuboid = l × b × h; where l, b and h represent the length, breadth and height of the cuboid.
Volume of Cube = s³; where s represents the side of the cube.
Volume of Cylinder = Πr²h; where h represents the height and r represents the radius of the cylinder.
Volume of a Hollow Cylinder = Π. h(R² – r²), where R = outer radius, r = inner radius
Volume of a normal square pyramid = (1/3) x h x s², where s = length of one of the sides of a square base and h is the height of the pyramid

Basic Geometry Formulas

The basic geometry formulas are important for every person whether they are preparing for the board exams or any other competitive exam. These formulas have applications in almost all the sector, ranging from engineering to statistics. Concepts regarding these formulas are even asked in the aptitude section of various government and private jobs. These basic formulas related to 2D and 3D geometrical figures are stated hereunder.

Perimeter of a Square = 4 × Side
Perimeter of a Rectangle = 2 × (Length + Breadth)
Area of a Square = Side²
Area of a Rectangle = Length × Breadth
Area of a Triangle = ½ × Base × Height
Area of a Trapezoid = ½ × (Base₁ + Base₂) × Height
Area of a Circle = A = π × r²
Circumference of a Circle = 2πr
Curved Surface Area of a Cylinder = 2πrh
Total Surface Area of a Cylinder = 2πr(r + h)
Volume of a Cylinder = V = πr²h
Curved Surface Area of a Cone = πrl
Total Surface Area of a Cone = πr(r + l) = πr[r + √(h² + r²)]
Volume of a Cone = V = ⅓ × πr²h
Surface Area of a Sphere = S = 4πr²
Volume of a Sphere = V = 4/3 × πr³

In all the above formulas,

h corresponds to height,

r corresponds to the radius,

l = slant height

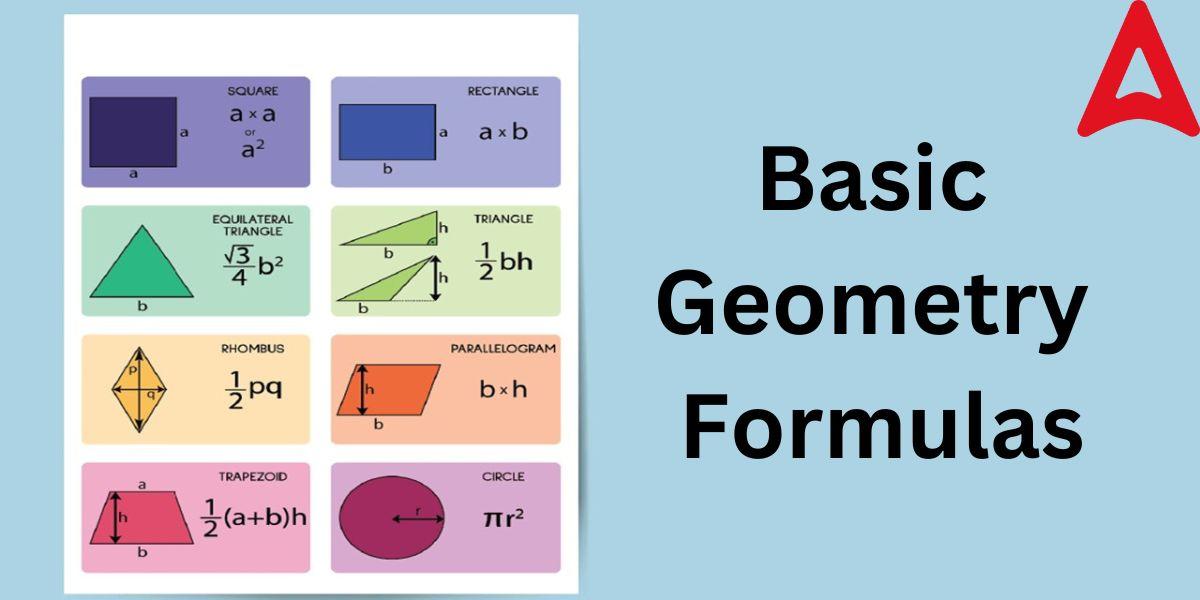
2D Geometry Formulas

As we know, 2D geometrical figures are those figures that have only two dimensions. Knowing the formula to compute different attributes of these figures is highly important. For this purpose, below we have mentioned all the relevant 2D geometry formulas.

2D Shape	Area Formula	Perimeter Formula
Square	a²	4a
Circle	π r²	2πr
Rectangle	l × b	2 ( l+ b )
Triangle	½ (b × h)	a + b + c
Right angle Triangle	½ (b × h)	b + hypotenuse +h
Equilateral Triangle	√(3/4) × a²	3a
Rhombus	½ ×d1 ×d2	4 × side
Parallelogram	b × h	2 ( l+ b )
Trapezium	½ h(a + b)	a + b + c + d

3D Geometry Formulas

3D shapes are named so because they consist of three dimensions that are length, breadth and height. 3D shapes are found in the nature everywhere. So, to solve real-world problems, it is of utmost importance to learn these formulas. So, we have tabulated the most useful 3D geometry formulas below.

Shape	Volume	Curved or Lateral surface area	Total surface area
Cube	a³	4a²	6a²
Cone	(⅓) π r² h	π r l	Π r (r + l)
Cylinder	π r² h	2π r h	2πrh + 2πr²
Hemisphere	(⅔) π r³	2 π r²	3 π r²
Cuboid	l × b× h	2 h( l+ b )	2 ( lb+ bh+ hl )
Sphere	(4/3) π r³	4 π r²	4 π r²
Frustum of Cone	(1/3)Πh(R² + R. r + r²)	Π (R + r)l	π[(R + r)l+r²+R²]