As per the Schedule, The Central Board of Secondary Education (CBSE) has conducted the CBSE Class 10 Maths Exam 2024 for basic and standard levels today, March 11. The CBSE Both tests began at 10:30 a.m. and ended at 1:30 p.m. After the exam, we are going to provide the Class 10 Maths Answer Key along with a detailed explanation. The CBSE Class 10 Mathematics Answer Key 2024 is created by highly skilled specialists, and all of the answers are correct and error-free. Stay connected and refresh the page to receive the latest Class 10 math exam questions and answers as soon as possible.
Class 10 Maths Answer Key 2024
The CBSE Class 10 Maths exam Exam is now over at 01:30 P.M. After reaching home from the center, Students rush to find the CBSE Class 10 Maths Answer key 2024 on the Internet. Using the Class 10 Maths Answer Key 2024, students may compare their answers to all of the questions on the exam and forecast their grades. Our professionals are prepared to supply maths Class 10 Answer Key 2024 to students, so they do not need to visit other websites. Students should bookmark this page and visit it frequently since we publish CBSE Maths answer key 2024 for all sets before anyone else.
CBSE Class 10 Maths Answer Key 2024
The CBSE Board will hold the Math Exam for the basic and standard levels for a total of 80 points each, with 20 marks for internal assessment. The exam will last three hours, and candidates will have an additional 15 minutes to peruse the question paper. The exam writing time will begin at 10:30 a.m. Check out the highlights of the CBSE Class 10 Maths Exam in the table below:
| Particulars | Details |
| Exam Conducting Body |
Central Board of Secondary Education (CBSE)
|
| Name of Examination |
CBSE Class 10 Board Examination 2024
|
| Subject | Mathematics |
| Mode of Exam | Offline |
| Exam Duration | 3 Hours |
| Medium of Exam | English / Hindi |
| Type of Questions |
MCQs, Short and Long Answer Type Questions
|
| Passing Marks | 33% in aggregate |
| Theory Marks | 80 |
| Practical Marks | 20 |
| Total Marks | 100 |
| Number of Sections | 5 Sections |
| Negative marking | No |
Class 10 Maths Answer Key 2024 of All Standard and Basic
If you are looking for the Class 10th Maths Answer Key 2024, you can stop the search here. Following the CBSE Class 10 Maths Exam, we will offer the detailed, 100% authentic CBSE Class 10 Maths Answer key 2024 for all sets as soon as possible. Our in-house experts are continually reviewing the Maths solution keys for all sets in depth. Stay connected to us.
Class 10 Maths Answer Key 2024 Set 1
QP- 30/5/1
SECTION A
This section comprises Multiple Choice Questions (MCQs) of 1 mark each. 20×1=20
1. The next (4th) term of the A.P. √18, √50, √98, is:
(A) √128
Answer:
(B) √140
(D) √200
Answer: Answer:
2. If 3 = 2 sin A, 3 = 2 cos A, then the value of x2 + y2 is:
(A) 36
(B) 9
(C) 6
(D) 18
Answer: (A) 36
3. If 4 sec θ – 5 = 0, then the value of cot θ is:
(A) 3/4
(C) 5/3
(B) 4 /5
(D) 4/ 3
Answer: (D) 4/ 3
4. Which out of the following type of straight lines will be represented by the system of equations 3x + 4y = 5 and 6x + 8y = 7 ?
(A) Parallel
(B) Intersecting
(C) Coincident
(D) Perpendicular to each other
Answer: (A) Parallel
5. The ratio of the sum and product of the roots of the quadratic equation 5×2-6x+21 = 0 is :
(A) 5:21
(C) 21:5
(B) 2:7
(D) 7:2
Answer: (B) 2:7
6. For the data 2, 9, x + 6, 2x + 3, 5, 10, 5; if the mean is 7, then the value of x is:
(A) 9
(B) 6
(C) 5
(D) 3
Answer: (D) 3
7. One ticket is drawn at random from a bag containing tickets numbered 1 to 40. The probability that the selected ticket has a number which is a multiple of 7 is:
(A) 1/7
(C) 1 /5
(B) 1/ 8
(D) 7/ 40
Answer: (B) 1/ 8
8. The perimeter of the sector of a circle of radius 21 cm which subtends an angle of 60° at the centre of circle, is:
(A) 22 cm
(B) 43 cm
(C) 64 cm
(D) 462 cm
Answer: (C) 64 cm
9. The length of an arc of a circle with radius 12 cm is 10 cm. The angle subtended by the arc at the centre of the circle, is :
(A) 120°
(B) 6°
(C) 75°
(D) 150°
Answer: (D) 150°
10. The greatest number which divides 281 and 1249, leaving remainder 5 and 7 respectively, is :
(A) 23
(B) 276
(C) 138
(D) 69
Answer: (C) 138
11. The number of terms in the A.P. 3, 6, 9, 12, …, 111 is:
(A) 36
(C) 37
(B) 40
(D) 30
Answer: (C) 37
12. A chord of a circle of radius 10 cm subtends a right angle at its centre. The length of the chord (in cm) is :
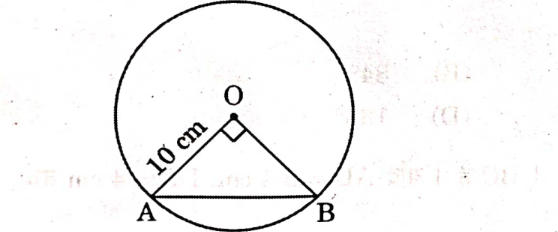
(A) 5√2
(B) 10/2
(C) 5 √2
(D) 5
Answer: (B) 10/2
13. The LCM of three numbers 28, 44, 132 is:
(A) 258
(B) 231
(C) 462
(D) 924
Answer: (D) 924
14. If the product of two co-prime numbers is 553, then their HCF is :
(A) 1
(C) 7
(B) 553
(D) 79
Answer: (A) 1
15. If a and ẞ are the zeroes of the polynomial p(x) = kx² – 30x + 45k and α + β = αβ, then the value of k is :
(A) -2/3
(C) 3/2
(B) -3/2
(D) 2/3
Answer: (D) 2/3
16. In the given figure, RJ and RL are two tangents to the circle. If RJL = 42°, then the measure of ✓ JOL is:
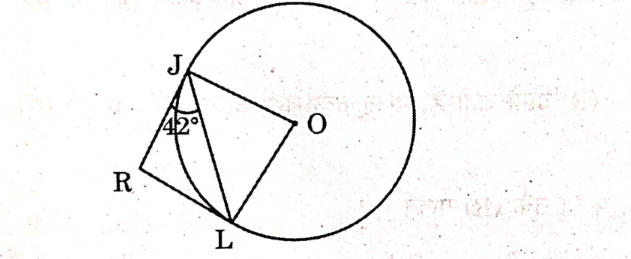
(A) 42°
(B) 84°
(C) 96°
(D) 138°
Answer: (B) 84°
17. In the given figure, in A ABC, DE || BC. If AD = 2.4 cm, DB = 4 cm and AE = 2 cm, then the length of AC is :
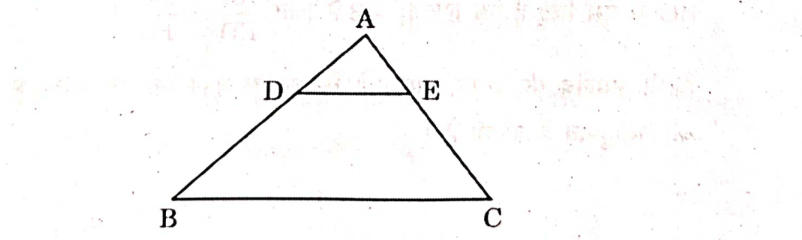
(A)10/3 cm
(B) 3/10cm
(C) 16/3 cm
(D) 1.2 cm
Answer: (C) 16/3 cm
18. If a vertical pole of length 7.5 m casts a shadow 5 m long on the ground and at the same time, a tower casts a shadow 24 m long, then the height of the tower is:
(A) 20 m
(B) 40 m
(C) 60 m
(D) 36 m
Answer: (D) 36 m
19. Assertion (A): ABCD is a trapezium with DC || AB. E and F are points on AD and BC respectively, such that EF || AB. Then AE / ED =BF/FC
Reason (R): Any line parallel to parallel sides of a trapezium divides the non-parallel sides proportionally.
Answer: (A)
20. Assertion (A): Degree of a zero polynomial is not defined.
Reason (R):Degree of a non-zero constant polynomial is 0.
Answer: (B)
CBSE Class 10 Maths Standard Answer Key 2024 for QP Code: 30/4/1
1. If ax + by = a²-b² and bx + ay = 0, then the value of x + y is:
Answer: (C) a-b
2. The HCF of two numbers 65 and 104 is 13. If LCM of 65 and 104 is 40x, then the value of x is:
Answer: (B) 13
3. If a polynomial p(x) is given by p(x) = x²- 5x + 6, then the value of p(1) + p(4) is:
Answer: (B) 4
4. If the discriminant of the quadratic equation 3x² – 2x + c = 0 is 16, then the value of c is:
Answer: (C) -1
5. If an arc subtends an angle of 90° at the centre of a circle, then the ratio of its length to the circumference of the circle is :
Answer: (B) 1:4
6. The area of the sector of a circle of radius 12 cm is 60 cm². The central angle of this sector is :
Answer: (D) 150°
7. If the difference of mode and median of a data is 24, then the difference of its median and mean is:
Answer: (A) 12
8. Two dice are tossed simultaneously. The probability of getting odd numbers on both the dice is:
Answer: (D) 9/36
8. Two dice are tossed simultaneously. The probability of getting odd numbers on both the dice is :
Answer: (D) 9/36
9. The ratio of total surface area of a solid hemisphere to the square of its radius is:
Answer: (C) 3π : 1
10. If sine = 1, then the value of [(1/2)*(sin(0/2))] is:
Answer: (A) 1/2/2
11. Two lines are given to be parallel. The equation of one of these lines is 5x – 3y = 2. The equation of the second line can be :
Answer: (D) 15x9y = 5
12. Three numbers in A.P. have the sum 30. What is its middle term?
Answer: (B) 10
13. In A ABC, DE || BC (as shown in the figure). If AD = 4 cm, AB = 9 cm and AC = 13.5 cm, then the length of EC is:
Answer: (B) 7.5 cm
14. At some time of the day, the length of the shadow of a tower is equal to its height. Then, the Sun’s altitude at that time is :
Answer: (B) 45°
15. In the given figure, AB and AC are tangents to the circle. If ∠ABC = 42°, then the measure of BAC is:
Answer: (A) 96°
16. The fourth vertex D of a parallelogram ABCD whose three vertices are A(-2, 3), B(6, 7) and C(8, 3) is:
Answer: (B) (0, -1)
17. For an event E, if P(E) + P(E) = q, then the value of q² – 4 is:
Answer: (A) -3
18. In the given figure, QR is a common tangent to the two given circles touching externally at A. The tangent at A meets QR at P. If AP = 4.2 cm, then the length of QR is :
Answer: (C) 8.4 cm
19. Assertion : Mid-point of a line segment divides the line segment in the ratio 1: 1.
Reason (R): The ratio in which the point (-3, k) divides the line segment joining the points (-5, 4) and (-2, 3) is 1: 2.
Answer: (C) Assertion (A) is true, but Reason (R) is false.
20. Assertion (A): If the circumference of a circle is 176 cm, then its radius is 28 cm.
Reason (R): Circumference = 2 x radius of a circle.
Answer: (A) Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of the Assertion (A).
CBSE Class 10 Maths Answer Key 2024 Set 2
QP- 30/5/2
SECTION A
This section comprises Multiple Choice Questions (MCQs) of 1 mark each. 20×1=20
1. If a and ẞ are the zeroes of the polynomial p(x) = kx²- 30x + 45k and α + β = aẞ, then the value of k is:
(A) – 2/3
(B) 3 /2
(C) -3/2
(D) 2 /3
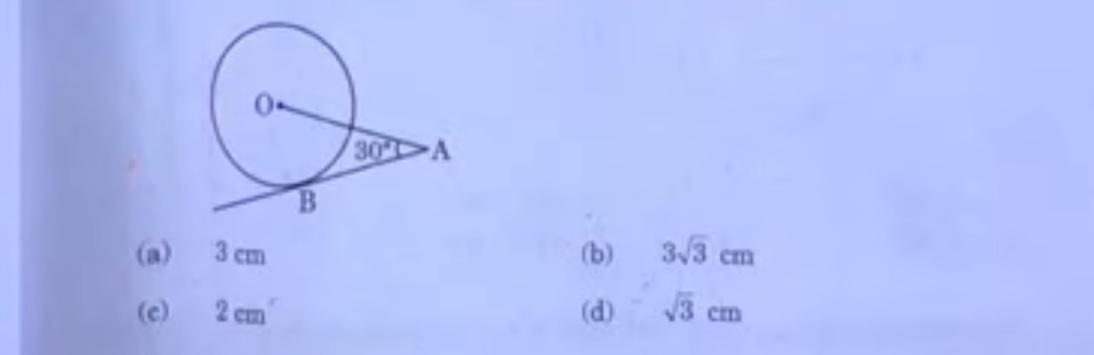
2. A chord of a circle of radius 10 cm subtends a right angle at its center. The length of the chord (in cm) is :

(A) 5√2
(C) 5/√2
(B) 10/2
(D) 5
3. The next (4th) term of the A.P. √7, √28, √63, is:
(A) √70
(B) √84
(C) √97
(D) √112
4. If the product of two co-prime numbers is 553, then their HCF is :
(A) 1
(B) 553
(C) 7
(d) 79
5. If x = a cos 0 and y = b sin 0, then the value of b²x² + a2y² is:
(A) a²b²
(B) ab
(9) a4b4
(D) a² + b²
6. If the quadratic equation ax2 + bx + c = 0 has real and equal roots, then the value of c is:
(A) b /2a
(B) -b /2a –
(C) b²/ 4a
(D) -b²/ 4a
7. In the given figure, in A ABC, DE || BC. If AD = 2.4 cm, DB = 4 cm and AE = 2 cm, then the length of AC is :
(A) 10/3 cm
(C) 16/3 cm
(B) 3/10cm
(D) 1.2 cm
8. The length of an arc of a circle with radius 12 cm is 10 cm. The angle subtended by the arc at the centre of the circle, is :
(A) 120°
(C) 75°
(B) 6°
(D) 150°
9. If 4 sec 0-5 = 0, then the value of cot 0 is:
(A) 3/4
(B) 4/5
(C) 5/3
(D) 4/3
10. The perimeter of the sector of a circle of radius 21 cm which subtends an angle of 60° at the center of circle, is:
(A) 22 cm
(B) 43 cm
(C) 64 cm
(D) 462 cm
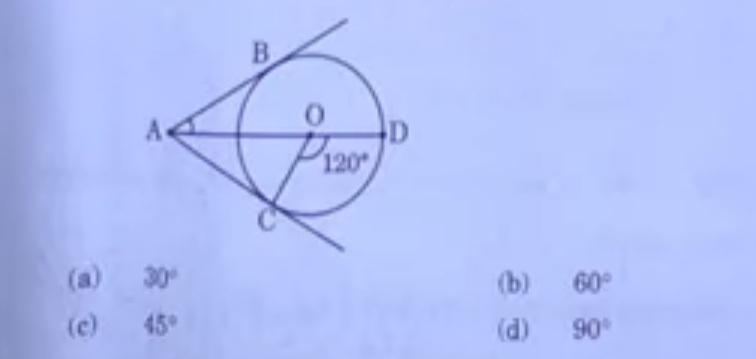
11. In the given figure, RJ and RL are two tangents to the circle. If RJL = 42°, then the measure of ✓ JOL is:

(A) 42°
(B) 84°
(C) 96°
(D) 138°
12. If the prime factorisation of 2520 is 23 x 3a × b x 7, then the value of a + 2b is:
(A) 12
(C) 9
(B) 10
(D) 7
13. Which out of the following type of straight lines will be represented by the system of equations 3x + 4y = 5 and 6x + 8y = 7 ?
(A) Parallel
(B) Intersecting
(C) Coincident
(D) Perpendicular to each other
14. One ticket is drawn at random from a bag containing tickets numbered 1 to 40. The probability that the selected ticket has a number which is a multiple of 7 is:
(A) 1/7
(C) 1/5
(B) 1/8
(D) 7/40
15. The LCM of three numbers 28, 44, 132 is:
(A) 258
(C) 462
(B) 231
(D) 924
16. The number of terms in the A.P. 3, 6, 9, 12, …, 111 is:
(A) 36
(C) 37
(B) 40
(D) 30
17. The ratio of the length of a pole and its shadow on the ground is 1 : √3. The angle of elevation of the Sun is :
(A) 90°
(B) 60°
(C) 45°
(D) 30°
18. If the mean and mode of a data are 24 and 12 respectively, then its median is:
(A) 25
(2) 20
(B) 18
(D) 22
CBSE Class 10 Maths Paper Analysis 2024
In the CBSE Class 10 Math Paper Analysis 2024. We evaluate the question paper based on the number of incorrect questions, the amount of questions that are not on the syllabus, and the difficulty level of the question paper. We provided a section-by-section analysis of the Class 10 Mathematics Paper based on feedback from students and professionals in this part.
| Parameter |
CBSE Class 10 Maths Exam Analysis
|
| Overall difficulty level of the paper | Moderate |
| Difficulty level of Section A | Easy |
| Difficulty level of Section B | Easy to Moderate |
| Difficulty level of Section C | Easy to Moderate |
| Difficulty level of Section D | Moderate |
| Difficulty level of Section E | Moderate |
| Overall expected a good score | To be Updated |
CBSE Class 10 Maths Exam 2024 -Student’s Reviews
We talked to the students who appeared in Today’s Exam, Several students have expressed varying opinions about the difficulty level of the CBSE Class 10 Maths exam.
- While some found the paper doable and within their expectations, others were challenged by specific questions, particularly those involving sophisticated computations and application-based challenges.
- Many students rated the exam as Easy, but they hoped for more clarity in some of the problems. Overall, students are optimistic that their preparation efforts will produce satisfactory outcomes.
Maths Answer Key & Marking Scheme
The CBSE Class 10 Maths Answer Key 2024 and marking scheme might assist pupils in forecasting their exam scores. Check out the Class 10 Maths Paper Marking Scheme tabulated below.
- The theory paper of class 10 basic and standard level exams is held for a total of 80 points each.
- The CBSE 10th maths question paper will consist of five sections: A, B, C, D, and E.
- Section A contains 20 multiple-choice questions (MCQs) worth one mark each.
- Section B consists of five short answer-I (SA-I) questions worth two points each.
- Section C includes six short answer-II (SA-II) questions for three points each.
- Section D consists of four long answer (LA) questions worth five marks each.
- Section E comprises three units of assessment of four marks each: source-based, case-based, passage-based, or integrated, with sub-parts worth one, one, and two marks each.
Class 10 Maths Board Paper 2024 PDF Download
CBSE Class 10 Math Papers 2024 will be available here. Candidates can predict their results by obtaining the Class 10 SST Question Papers and reading the Class 10 Maths Answer Key 2024.
| CBSE Class 10 Maths Question Paper 2024 Pdf Download | |
| CBSE Maths Paper Class 10 2024 Set 1 (30/5/1) | Download PDF |
| CBSE Class 10 Board Maths Paper 2024 Set 2 | Download PDF |
| CBSE Class 10 Maths Question Papers 2024 Set 3 | Download PDF |
| CBSE Maths Paper Class 10 2024 Set 1 (30/3/1) | Download PDF |
Class 10 Standard Maths Answer key with Solutions (Last Year)
Section A
This section comprises multiple choice questions (MCQ) of 1 mark each.
4. In the given figure, DE || BC. The value of x is
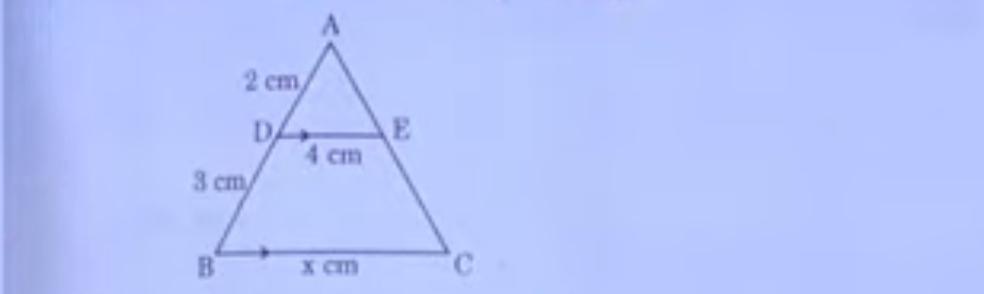


Answer: (c) 6.5 cm
9. Water in a river which is 3 m deep and 40 m wide is flowing at the rate of 2 km/h. How much water will fall into the sea in 2 minutes?


14. The 11th term from the end of the A.P.: 10, 7, 4, 62 is:
17. Which of the following numbers cannot be the probability of happening of an event?
19 Find the sum of first 30 terms of AP: -30, 24, -18,/..
Solution: a= -30, d= 6
= 15 [-60 + 29 (6)]
= 15 [-60+174]
= 15 [114]
= 1710
OR
If an AP is Sn = n(4n+1), then find the AP
Solution: S1 = T1 = 5
S2= T1 + T2= 18
S2-S1 = T2= 13
AP= 5, 13, 21, 29, …
21. A solid metallic sphere of radius 10.5 cm is melted and recast into a number of smaller cones, each of radius 3.5 cm and height 3 cm. Find the number of cones so formed.
Solution: r1 = 10.5 cm (sphere) and r2 (cone)= 3.5 cm, h2= 3cm
4/3πr³ = n x 1/3πr2² h
4r³ = nr2² h
4 x (105/10)³= n x 35/10 x 35/10 x 3
21 x 6= n
Number of cones formed= 126
22. (a) Find the value of m for which the quadratic equation
(m-1) x² + 2(m-1)x + 1 = 0
Solution: D= 0
4 (m-1)² – 4(m-1) = 0
4 (m-1) [m-1-1]= 0
(m-1) (m-2)= 0
m= 2
(b) Solve the following quadratic equation for x: √3x² + 10x + 7√3= 0
Solution: √3x² + 3x + 7x + 7√3= 0
√3x (x+ √3) + 7 (x + √3)= 0
(x+ √3) [√3x + 7]= 0
x= √3 || x= -7/√3
23. Find the mode of the following frequency distribution:
| Class | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| Frequency | 15 | 10 | 12 | 17 | 4 |
Solution: l= 40, f1= 17, f2= 4, fo= 12
Mode= l + f1-fo / 2f1 – fo- f2
= 40 + 17-12 / 34-12-4 x 10
= 40 + 5/18 x 10
= 40 + 25/9
= 40 + 2.78
= 42.78
Q.5: The product of Rehan’s age (in years) 5 years ago and his age 7 years from now, is one more than twice his present age. Find his present age.
Solution:
| Past Age | Present Age | Future Age |
| x-5 | x | x+7 |
(x-5) (x+7) = 2x + 1
x² + 2x -35 = 2x+1
x² – 36 = 0
x² = 36
x= +_ 6
Present Age- 6 years
Q.6 Two concentric circles are of radii 4 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution:

Section B
Q.7: For what value of x, is the median of the following frequency distribution 34:5?
| Class | Frequency |
| 0-10 | 3 |
| 10-20 | 5 |
| 20-30 | 11 |
| 30-40 | 10 |
| 40-50 | x |
| 50-60 | 3 |
| 60-70 | 2 |
Solution:

Q.8: Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameter each at a distance of 7 cm from its centre. Construct tangents to the circle from these two points P and Q.
Solution:

Q.9: (a) The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, then find the height of the building.
Solution:
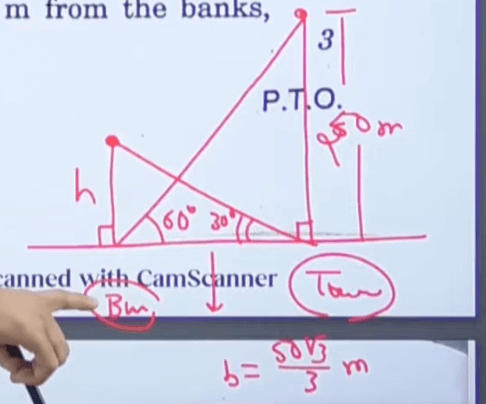
tan 60° = 50/b
b= 50/ tan 60°
b = 50/ √3
b= 50√3 / 3
tan 30° = h/(50√3/3)
h= 50√3/3 x 1/√3
= 50/3 m= 16.67 metres
OR
Q.9:(b) From a point on a bridge across a river, the angles of depression of the banks on opposite sides of the river are 30° and 45° respectively. If the bridge is at a height of 3 m from the banks, then find the width of the river.
Solution:
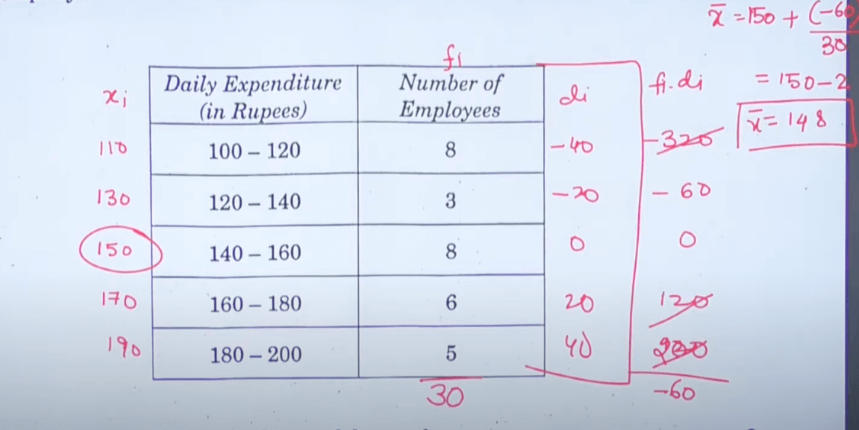
Q.10: Following is the daily expenditure on lunch by 30 employees of a company, Find the mean daily expenditure of the employees.
Solution:
Q.11: From a solid cylinder of the height of 30 cm and radius of 7 cm, a conical cavity of height of 24 cm and same radius is hollowed out. Find the total surface area of the remaining solid.
Solution: H= 30 cm
R= 7 cm
Total Surface Area of Cylinder = Curved Surface Area of Cylinder + Curved Surface Area of Cone + πr²
TSA = 2 πrh + πrl + πr²
= πr (2h+ l+ r)
= 22/7 x 7 (60+25 + 7)
= 22 x 92
TSA= 2024 cm
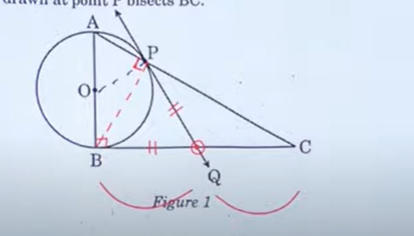
Q.12: In figure 1, a traingle ABC with angle B = 90 degrees is shown. Taking AB as diameter, a circle has been drawn intersecting AC at point P. Prove that the tangent drawn at point P bisects BC.
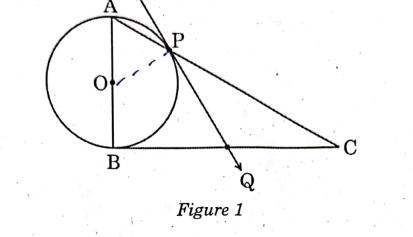
Solution:
Case Study:1
Q.13: In Mathematics, relations can be expressed in various ways. The matchstick patterns are based on linear relations. Different strategies can be used to calculate the number of matchsticks used in different figures.
One such pattern is shown below. Observe the pattern and answer the following questions using Arithmetic Progression::
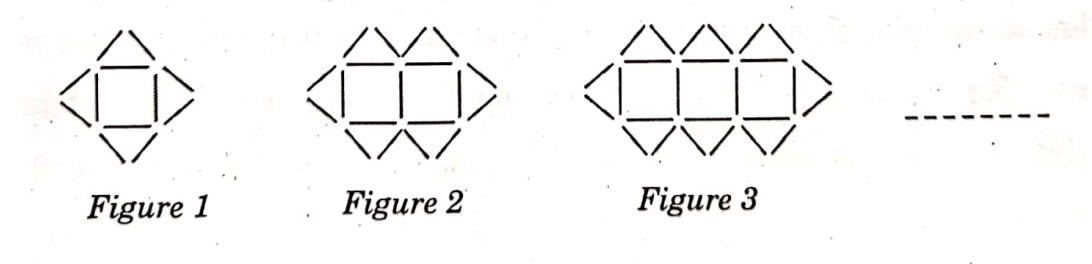
(a) Write the AP for the number of triangles used in the figures. Also, write the nth term of this AP. Which figure has 61 matchsticks?
Solution- AP = 4, 6, 8, 10
a= 4, d= 2
Tn = 4 + 2(n-1)
Tn= = 4 + 2n – 2
Tn= 2n +2
(b) Which figures has 61 matchstickes?
Solution: 12, 19, 26, …
Tn = 61
a + (n-1) d= 61
12 + 7(n-1) = 61
7(n-1) = 49
n-1 = 7
n= 8
8th figure has 61 matchsticks
Q.14 Gadisagar lake is located in the jaisalmer district of Rajasthan. It was built by king of jaisalmer ad rebuilt by Gadsi Singh in 14th Century. The lake has many chattris. One of them is shown below:

Observe the picture. From a point A h m above from water level, the angle of elevation of top of chattari (point B) is 45 degrees and angle of depression of its reflection in water(Point C) is 60 degrees. If the height of chhattri above the water level is 10m, then
a) Draw a well-labelled figure based on the above information;
b) Find the height of the point A above the water level.
(Use √3 = 1.73)
Solution:











 CUET UG Answer Key 2025 (Provisional) Re...
CUET UG Answer Key 2025 (Provisional) Re...
 IISER Final Answer Key 2025 Out, Downloa...
IISER Final Answer Key 2025 Out, Downloa...
 OUAT Answer Key 2025 OUT @ouat.ac.in, Do...
OUAT Answer Key 2025 OUT @ouat.ac.in, Do...









