CBSE Class 12 Mathematics Previous Year Question Papers With Solutions

Mathematics as a subject is crucial for students belonging to both the commerce and science domains. The marks scored in class 12 of mathematics subject plays an important role in the further admission process of students. It is therefore necessary to increase the Class 12 Maths marks. In this process, students must solve the previous year question papers of the Mathematics subject. Along with the CBSE Class 12 Maths Question Paper 2023, previous year’s CBSE 12th Math question papers are provided here.

Class 12 Mathematics Previous Year Question Paper

The Class 12 Mathematics Previous Year Question Paper will help students to understand the pattern of questions. The Central Board of Secondary Education does repeat the Class 12 Mathematics Previous Year Question Paper. The students must practice Class 12 Mathematics Previous Year Question Paper given on this page to get extra marks in CBSE Class 12 board Exam 2024.

We have given Class 12 Mathematics Previous Year Question Paper with solutions so students will know the framing of answers and get good marks in the final examination. Through this, students will also be able to achieve a solid foundation in the Mathematics subject for pursuing engineering or commerce-related courses. Bookmark this page to get all the important updates from the Central Board of Secondary Education.

Maths Previous Year Question Paper Class 12 CBSE Board

The CBSE Class 12 Maths Previous Year Paper is regarded as an essential resource for students preparing for the board exam. In later classes, one can apply the skills learned in CBSE Class 12 to comprehend a variety of higher-level subjects. Therefore, students who want to work in mathematics must have good grades in their math classes. To help you reach this aim, you can solve the math paper from the previous year’s CBSE Class 12 provided below.

CBSE Class 12 Mathematics Question Paper 2023

CBSE Class 12 Mathematics Question Paper 2022

CBSE Class 12 Applied Mathematics Question Paper 2022

CBSE Previous Year Question Papers Class 12 Maths with Solutions

The previous year question paper solutions for different academic years’ Maths paper is provided in this article. The solutions provided in this article will help students understand the art of deriving answers of the mathematical questions based on the latest marking scheme. The solution for the CBSE Class 12 Mathematics board exam paper 2023 is given below. The solutions for other previous year’s question papers of the Math exam is given ahead in this post.

CBSE Class 12 Maths Question Paper Solutions 2023

Mathematics Class 12 Previous Year Question Paper – 2020

Section – A

Question 1.
If A is a square matrix satisfying A’ A = I, write the value of |A|. 
Solution:
Given, A’ A= I

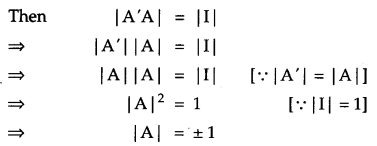
Question 2.
If y = x | x |, find dydx for x < 0. [1]
Solution:
If y = x | x |

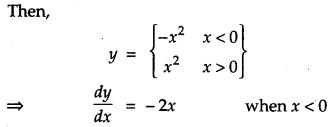
Question 3.
Find the order and degree (if defined) of the differential equation [1]

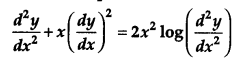
Solution:

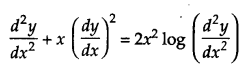
Order of this equation is 2.
Degree of this equation is not defined.

Question 4.
Find the direction consines of a line which makes equal angles with the coordinate axes. [1]
Solution :
Let the direction cosines of the line make an angle a with each of the coordinate axes and direction cosines be l, m and n.

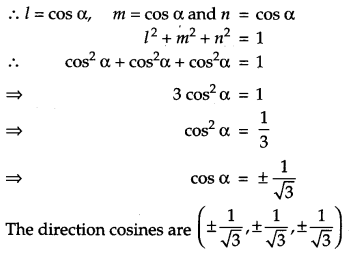
A line passes through the point with position vector 2i^−j^+4k^ and is in the direction of the vector i^+j^−2k^. Find the equation of the line in cartesian form.
Solution:
The line passes through a point (2, -1, 4) and has direction ratios proportional to (1, 1, – 2).
Cartesian equation of the line

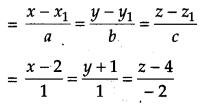
Section – B

Question 5.
Examine whether the operation * defined on R, the set of all real numbers, by a∗b=a2+b2−−−−−−√ is a binary operation or not, and if it is a binary operation, find whether it is associative or not.** [2]

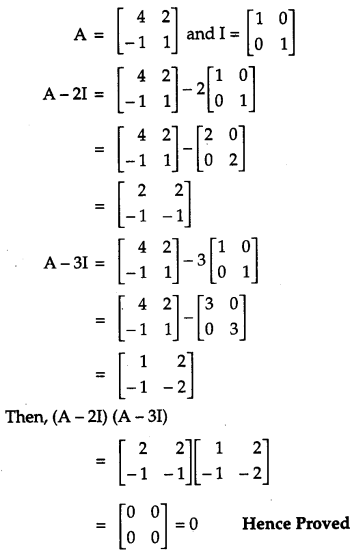
Question 6.
If A = [4−121], show that (A – 2I)(A – 3I) = 0. [2]
Solution:
Given,

Question 7.
Find: [2]

Solution:

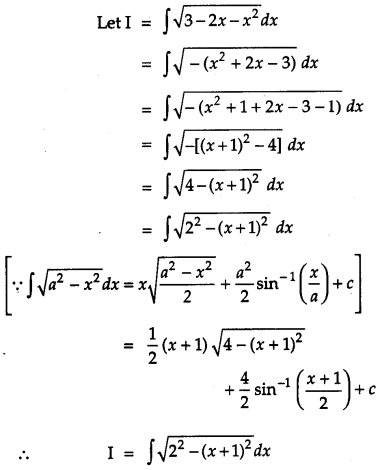
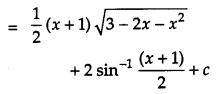
Question 8.
Find: [2]

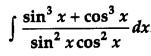
Solution:

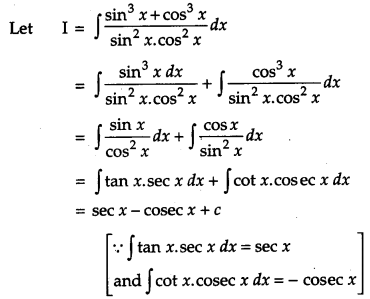
OR
Find:

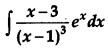
Solution:

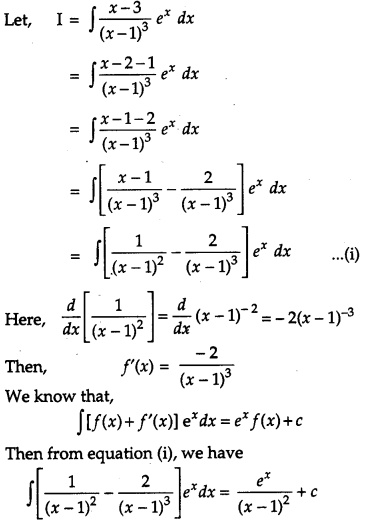
Question 9.
Find the differential equation of the family of curves y = Ac^2x + Be^-2x, where A and B are arbitrary constants. [2]
Solution:
Given, y = Ae^2x + Be^-2x (i)
On differentiating equation (i) w.r.t. x, we get

Q. Find the volume of a cuboid whose edges are given by −3i^+7j^+5k^,−5i^+7j^−3k^ and 7i^−5j^−3k^.
Solution:
If a, b, c are edges of a cuboid.

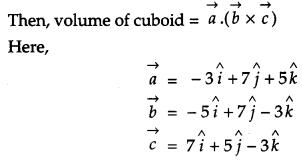
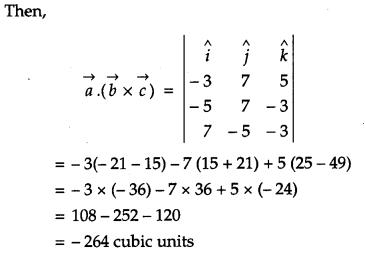
Question 11.
If P(not A) = 0·7, P(B) = 0·7 and P(B/A) = 0·5, then find P(A∆B). [2]
Solution:

Question 12.
A coin is tossed 5 times. What is the probability of getting (i) 3 heads, (ii) at most 3 heads? [2]
Solution:


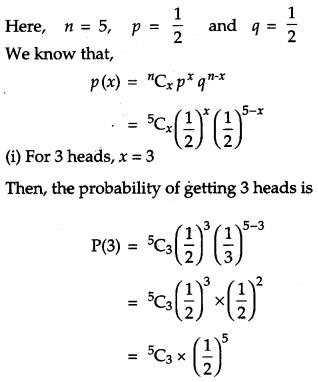
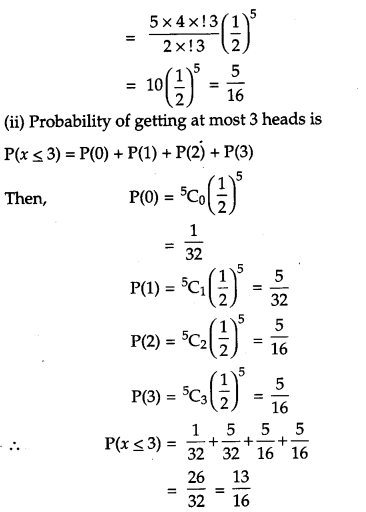
OR
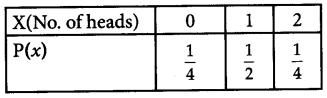
Find the probabilty distribution of X, the number of heads in a simultaneous toss of two coins.
Solution:
If we toss two coins simultaneously then sample space is given by (HH, HT, TH, IT)
Then probability distribution is,

Section – C

Question 13.
Check whether the relation R defined on the set A = {1, 2, 3, 4, 5, 6} as R = {(a, b) : b = a + 1} is reflexive, symmetric or transitive. [4]
Solution:
Here, R = {(a, b): b = a +1}
∴ R = {(a, a + 1): a, a + 1 ϵ (1, 2, 3, 4, 5 ,6)}
⇒ R = {(1, 2,) (2, 3), (3, 4), (4, 5), (5, 6)}
(i) R is not reflexive as {a, a} ∉ R∀a
(ii) R is not symmetric as (1, 2) ϵ R but (2, 1) ∉ R
(iii) R is not transitive as (1, 2) ϵ R, (2, 3) ϵ R but (1, 3) ϵ R
OR
Let f: N → Y be a function defined as f(x) = 4x + 3, where Y = {y ϵ N : y = 4x + 3, for some x ϵ N}. Show that f is invertible. Find its inverse.
Solution:
Consider an arbitrary element of Y. By the definition of y, y = 4x + 3, for some x in the domain N.

Question 14.
Find the value (cos−145+tan−123) [4]
Solution:
(cos−145+tan−123)

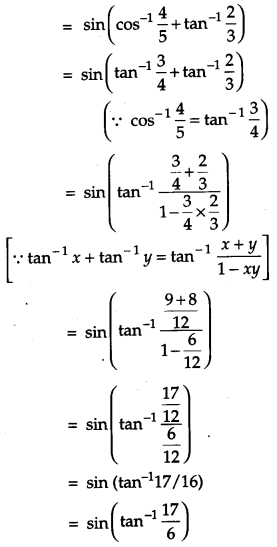
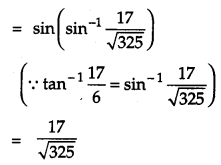
Question 15.
Using properties of determinants, show that [4]

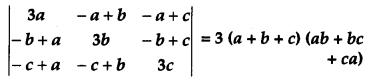
Solution:

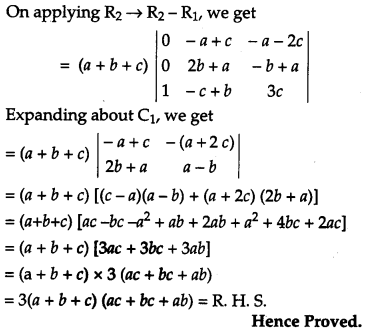
Question 16.
If x1+y−−−−√+y1+x−−−−√ = 0 and x ≠ y, prove that dydx=−1(x+1)2 [4]
Solution:

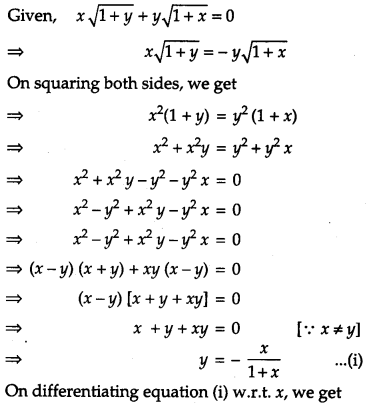
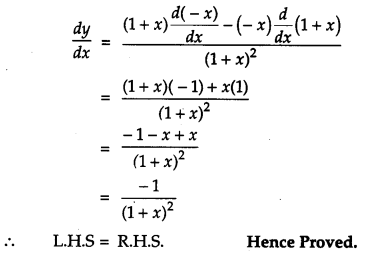
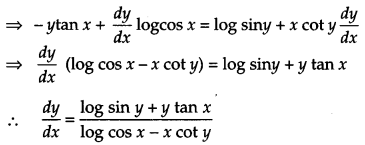
Question 17.
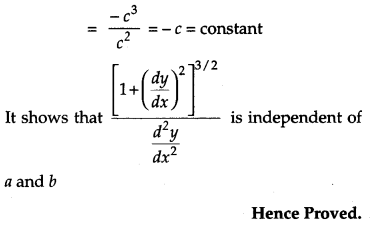
If If (x – a)² + (y – b)² = c², for some c > 0, prove that [1+(dydx)2]3/2d2ydx2 is a constant independent of a and b. [4]
Solution:

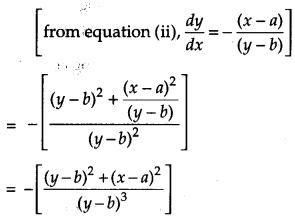
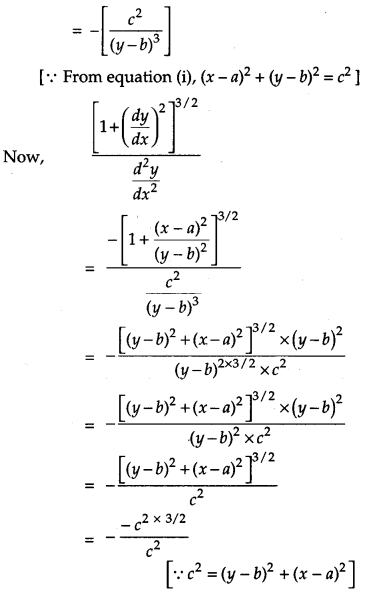
Question 18.
Find the equation of the normal to the curve x² = 4y which passes through the point (-1, 4). [4]
Solution:
Suppose the normal at P(x₁, y₁) on the parabola x² = 4y passes through (-1, 4)
Since, P(x₁, y₁) lies on x² = 4y
∴ x21 = 4y₁
The equation of curve is x² = 4y
Differentiating with respect to x, we have
2x = 4 dydx

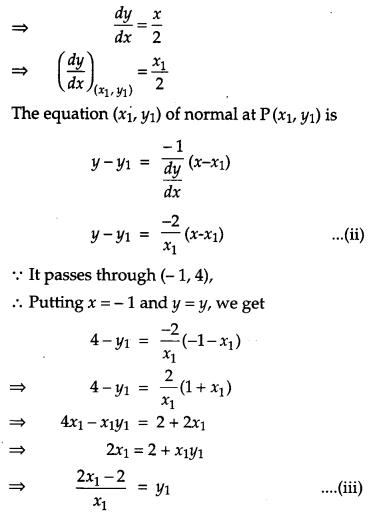
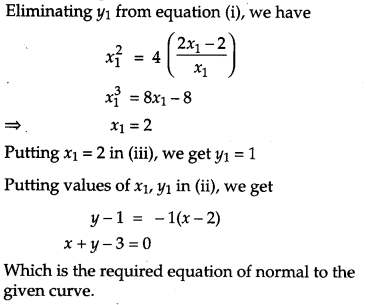
Question 19.
Find: [4]

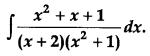
Solution:

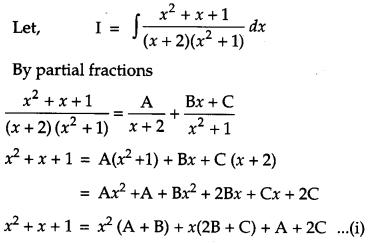
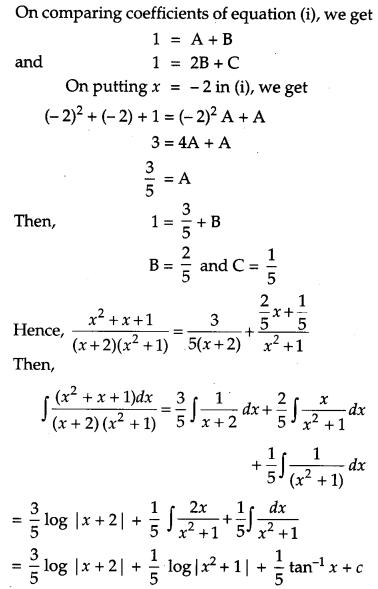
Question 20.
Prove that : ∫a0f(x)dx=∫a0f(a−x)dx and hence evaluate ∫π/20xsinx+cosxdx. [4]
Solution:

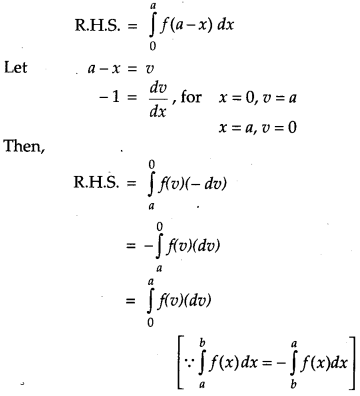
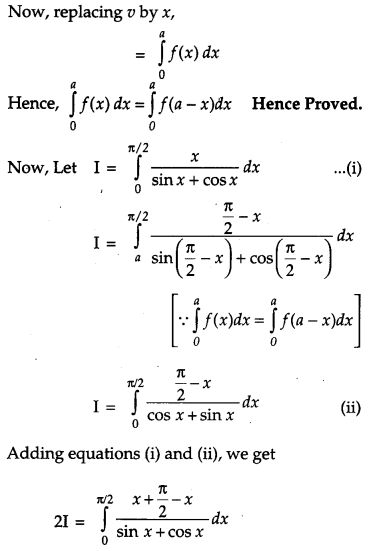
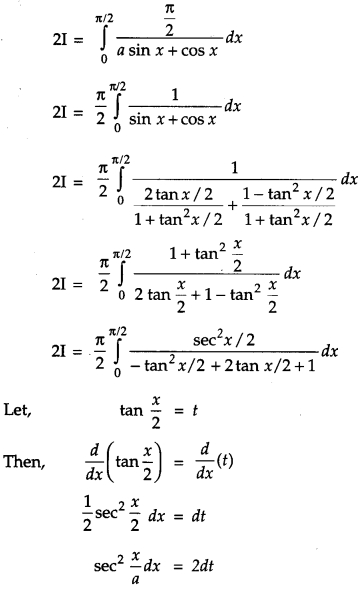
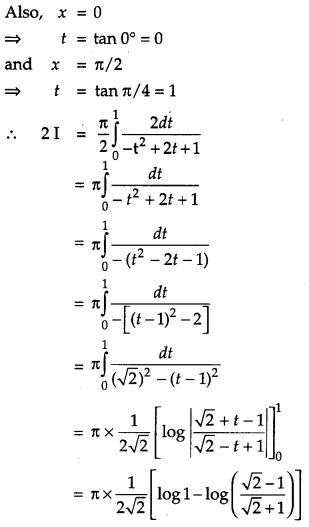
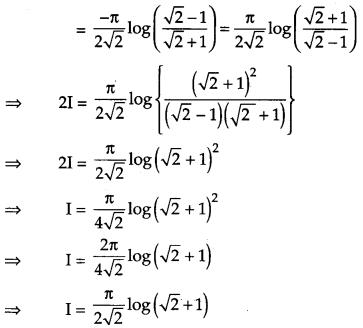
Question 21.
Solve the differential equation: [4]

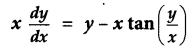
Solution:

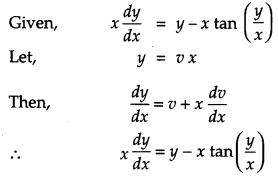
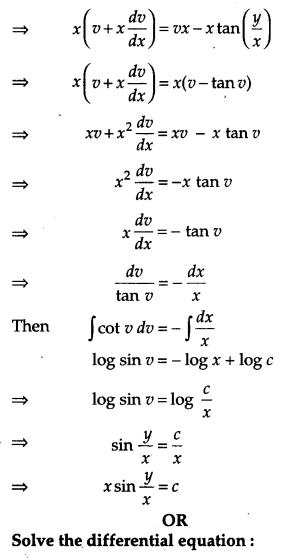
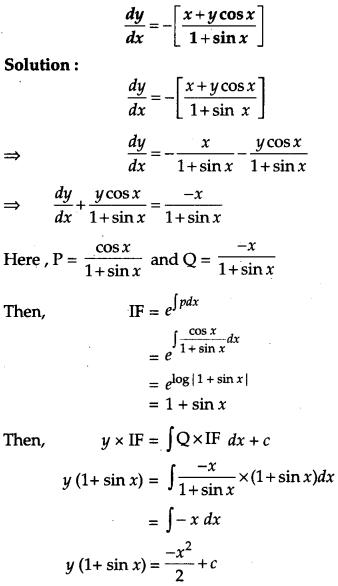
Question 23.
If the lines x−1−3=y−22λ=z−32 and x−13λ=y−12=z−6−5 are perpendicular, find the value of λ. Hence find whether the lines are intersecting or not. [4]
Solution:

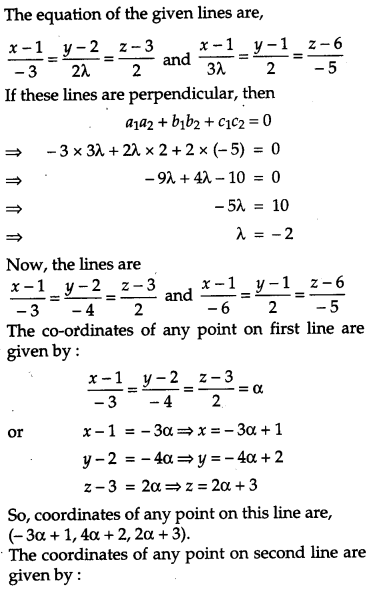
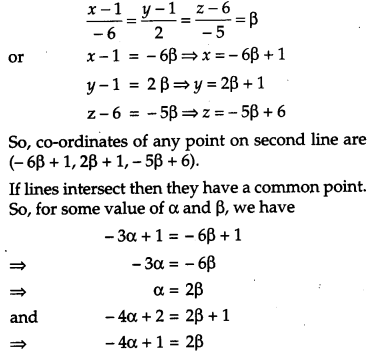
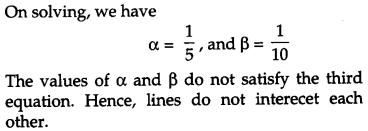
Section – D

Question 24.
If A = ⎡⎣⎢125311421⎤⎦⎥, find A^-1 [6]
Hence solve the system of equations
x + 3y + 4z = 8
2x + y + 2z = 5
and 5x + y + z = 7
Solution:




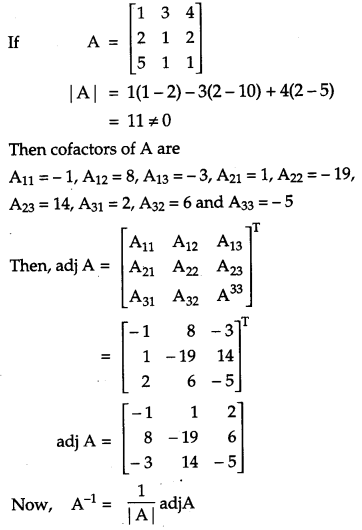
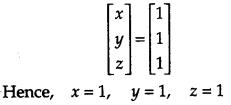
OR
Find the inverse of the following matrix, using elementary transformation:
A = ⎡⎣⎢250011−103⎤⎦⎥
Solution:

Question 25.
Show that the height the cylinder of maximum volume that can inscribed in a sphere of radius R is 2R3√. Also find the maximum volume. [6]
Solution:
Let, ‘x’ be the diameter of the base of the cylinder and let ‘h’ be height of the cylinder.

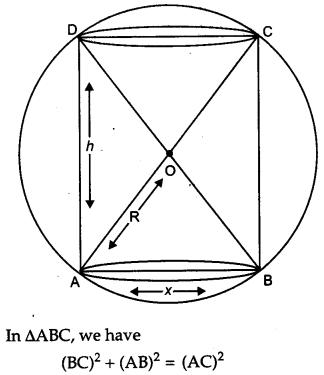
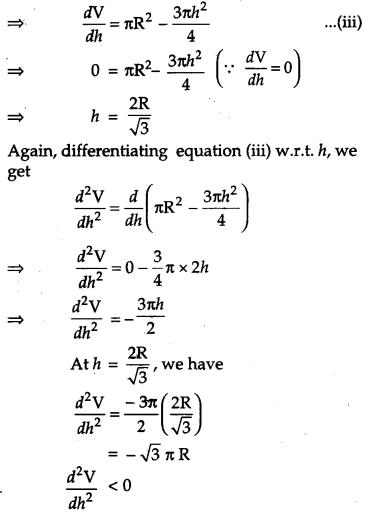
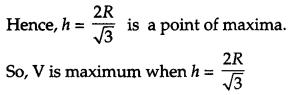
Question 26.
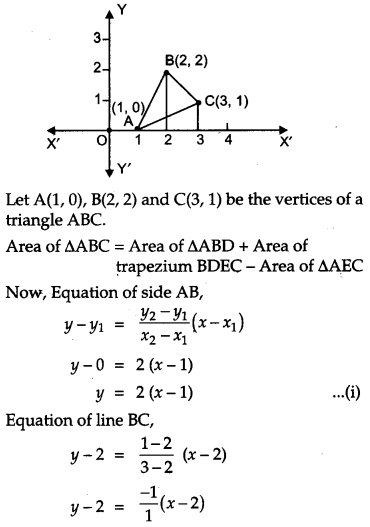
Using method of integration, find the area of the triangle whose vertices are (1, 0), (2, 2) and (3, 1). [6]
Solution:
A(1, 0), B(2, 2) and C(3, 1)


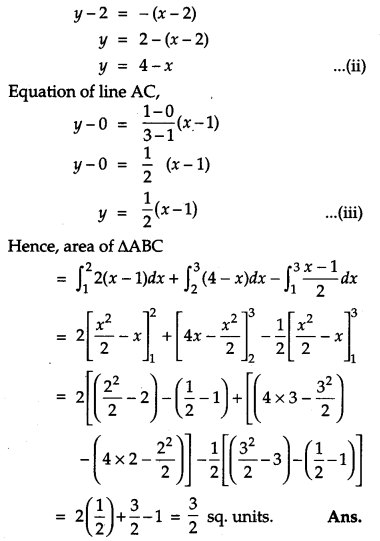
OR
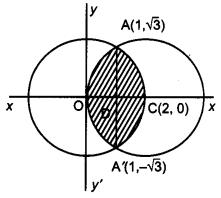
Using method of integration, find the area of the region enclosed between two circles x² + y² = 4 and (x – 2)² + y² = 4.
Solution:
Equations of the given circles are,
x² + y² = 4 …(i)
(x – 2)² + y² = 4 …(ii)
Equation (i) is a circle with centre O at the origin and radius 2. Equation (ii) is a circle with centre C (2, 0) and radius 2.
Solving equation (i) and (ii) we have
(x – 2)² + y² = x² + y²
or x² – 4x + 4 + y² = x² + y² or x = 1 which gives y = ±3–√
Thus, the points of intersection of the given circles are A (1, 3–√ ) and A'(1, 3–√ )

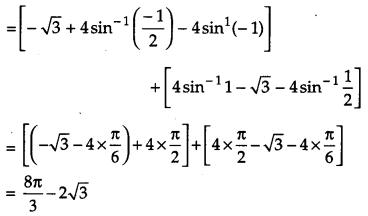
Question 27.
Find the vector and cartesian equations of the plane passing through the points having position vectors i^+j^−2k^,2i^−j^+k^ and i^+2j^+k^. Write the equation of a plane passing through a point (2, 3, 7) and parallel to the plane obtained above. Hence, find the distance between the two parallel planes. [6]
Solution :
Let A, B, C be the points with position




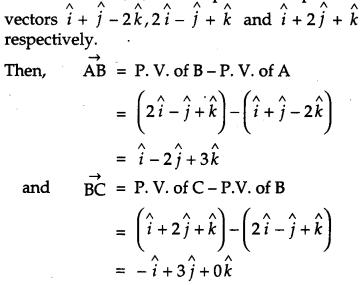
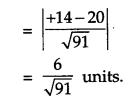
OR
Find the equation of the line pasing through (2, -1, 2) and (5, 3, 4) and of the plane passing through (2, 0, 3), (1, 1, 5) and (3, 2, 4). Also, find their point of intersection.
Solution:
We know that the equation of line passing through points (x₁, y₁, z₁) and(x₂, y₂, z₂) is given by

Question 28.
There are three coins. One is a two-headed coin, another is a biased coin that comes up heads 75% of the time and the third is an unbiased coin. One of the three coins is chosen at random and tossed. If it shows heads, what is the probability that it is the two-headed coin? [6]
Solution:
Given, there are three coins.
Let,
E₁ = coin is two headed
E₂ = biased coin
E₃ = unbiased coin
A = shows only head

Question 29.
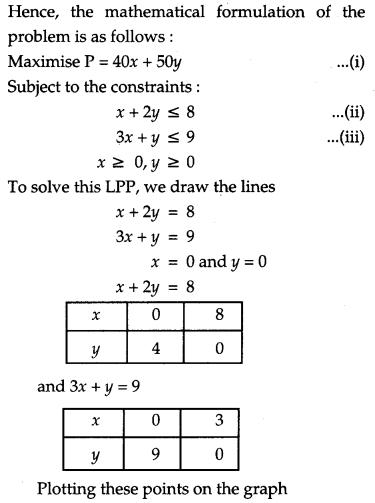
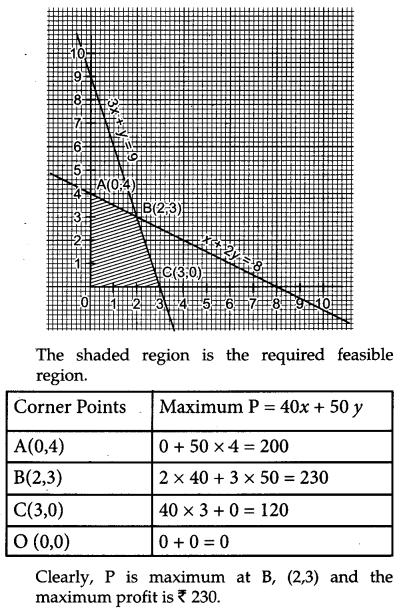
A company produces two types of goods, A and B, that require gold and silver. Each unit of type A requries 3g of silver and 1 g of gold while that of type B requires 1 g of silver and 2g of gold. The company can use at the most of 9 g of silver and 8 of gold. If each unit of type A brings a profit of ₹ 40 and that of type B ₹ 50, find the number of units of each type that the company should produce to maximize profit. Formulate the above LPP and solve it graphically and also find the maximum profit [6]
Solution:
There are two types of goods, A and B and let units of type A be x and units of type B be y.

Class 12 Mathematics Previous Year Question Paper – 2019

Section – A

Question 1.
Find the value of tan^-13–√ – cot^-1 (−3−−−√) [1]
Solution:
We have,

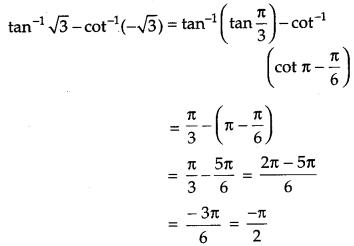
Question 2.
If the matrix A = ⎡⎣⎢02ba01−3−10⎤⎦⎥ is skew-symmetric, find the values of’a’ and ‘b’. [1]
Solution:

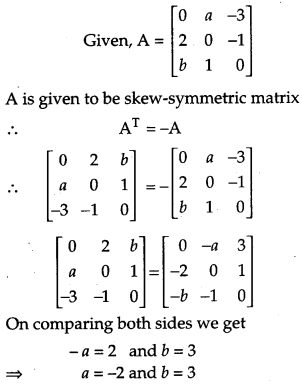
Question 3.
Find the magnitude of each of the two vectors a⃗  and b⃗ , having the same magnitude such that the angle between them is 60° and their scalar product is 92 . [1]
Solution:
Let a⃗  and b⃗  be two such vectors.

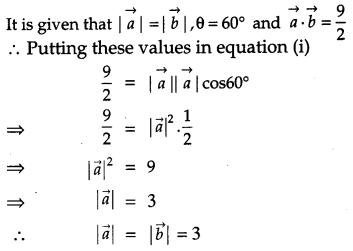
Question 4.
If a * b denotes the larger of ‘a’ and ‘b’ and if a o b = (a * b) + 3, then write the value of (5) o (10), where * and o are binary operations.** [1]

Section – B

Question 5.
Prove that: [2]

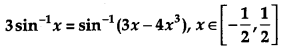
Solution:
R.H.S = sin^-1(3x – 4x³)
Putting x = sin θ in R.H.S, we get
R.H.S = sin^-1(3 sin θ – 4 sin³ θ)
= sin^-1(sin 3θ)

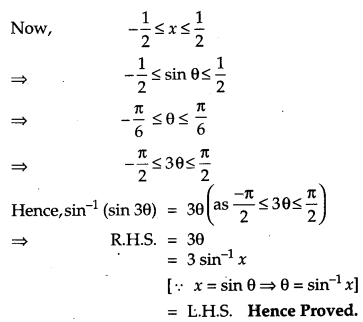
Question 6.
Given A = [2−4−37], compute A^-1 and show that 2A^-1 = 9I – A. [2]
Solution:

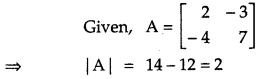
Question 7.
Differentiate tan−1(1+cosxsinx) with respect to x. [2]
Solution:

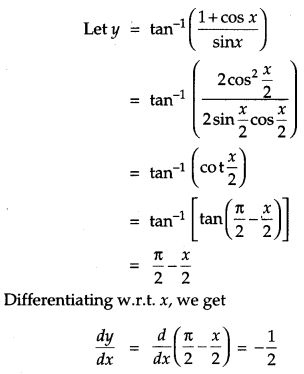
Question 8.
The total cost C(x) associated with the pro-duction of x units of an item is given by C(x) = 0.005x³ – 0.02x² + 30s + 5000. Find the marginal cost when 3 units are produced, where by marginal cost we mean the instantaneous rate of change of total cost at any level of output. [2]
Solution :
Cost function is given as
C(s) = 0.005x³ – 0.02x² + 30s + 5000
Marginal cost (MC) = ddx(C(x))
= 0.005(3x²) – 0.02 (2x) + 30
= 0.015x² – 0.04s+ 30
When x = 3,MC = 0.015(3)² – 0.04(3) + 30
= 0.135 – 0.12 + 30
= 30.015

Question 9.
Evaluate:

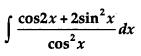
Solution:
We have,

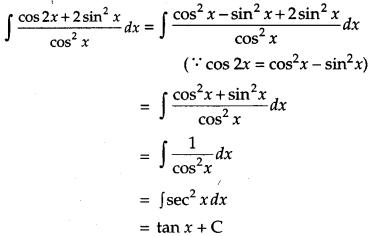
Question 10.
Find the differential equation representing the family of curves y = ae^{bx + 5}, where a and b are arbitrary constants. [2]
Solution:
Given curve is
y = ae^{bx + 5} …(i)
Differentiating (i) w.r.t. s, we get

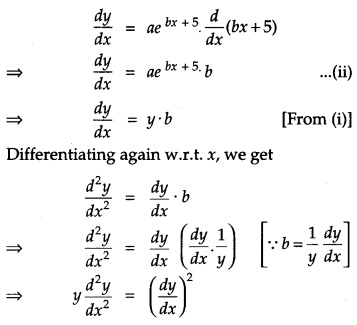
Question 11.
If θ is the angle between two vectors i^−2j^+3k^ and 3i^−2j^+k^, find sin θ. [2]
Solution:

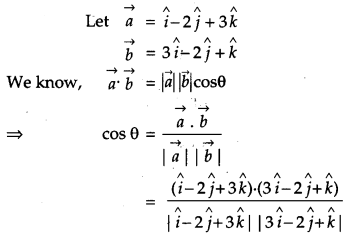
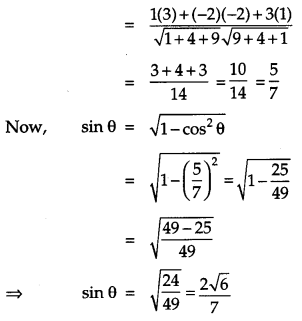
Question 12.
A black and a red die are rolled together. Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4. [2]
Solution :
The sample space has 36 Outcomes. Let A be event that the sum of observations is 8.
∴ A = {(2, 6), (3, 5), (5, 3), (4, 4), (6, 2)}

Section – C

Question 13.
Using properties of determinants, prove that: [4]

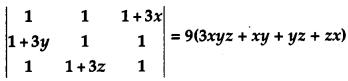
Solution:

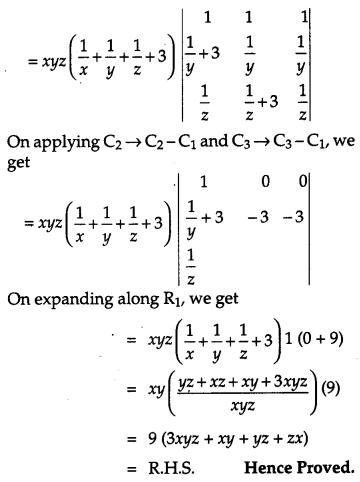
Question 14.
If (x² + y²)² = xy, find dydx. [4]
Solution:
We have,
(x² + y²)² = xy …(i)

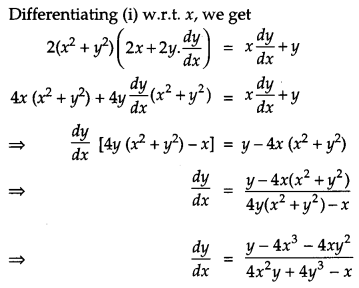
OR
If x = a(2θ – sin 2θ) and y = a(1 – cos 2θ), find dydx when θ = π3.
Solution:
Given, x = a (2θ – sin 2θ)
and y = a (1 – cos 2θ)
Differentiating x* and y w.r.t. θ, we get

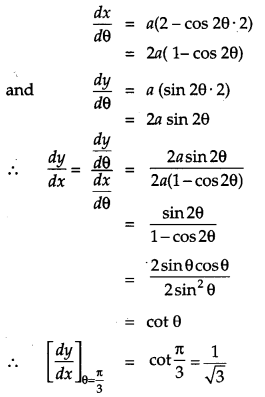
Question 15.
If y = sin(sin x), prove that: [4]

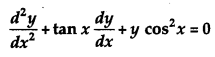
Solution:
Given, y = sin (sin x)
Differentiating y w.r.t. x, we get
dydx = cos (sin x) • cos x
Differentiating again w.r.t. x, we get
d2ydx2= cos (sin x) (- sin x) + cos x [-sin (sin x)-cos x]

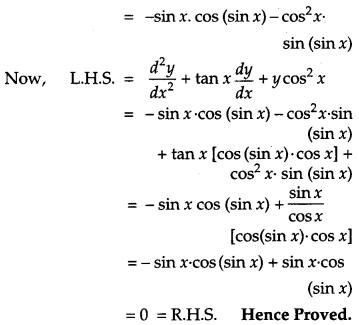
Question 16.
Find the equations of the tangent and the normal to the curve 16x² + 9y² = 145 at the point (x₁, y₁), where x₁ = 2 and y₁ > 0. [4]
Solution:
Given curve is
16x² + 9y² = 145 ….(i)
Since (x₁, y₁) lies on equation (i),



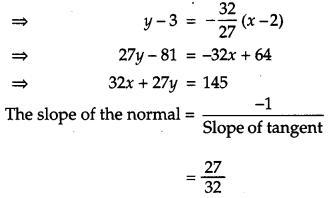
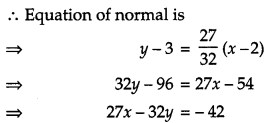
OR
Find the intervals in which the function

(a) strictly increasing,
(b) strictly decreasing.
Solution:
Given function is

Question 17.
An open tank with a square base and vertical sides is to be constructed from a metal sheet so as to hold a given quantity of water. Show that the cost of material will be least when depth of the tank is half of its width. If the cost is to be borne by nearby settled lower income families, for whom water will be provided, what kind of value is hidden in this question ? [4]
Solution:
Let the length, breadth and height of the open tank be x, x and y units respectively.
Then, Volume (V) = x²y …(i)


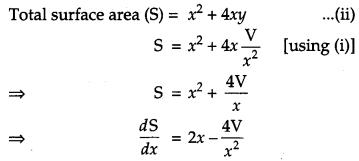
Area is minimum, thus cost is minimum when x = 2y.
i.e., depth of tank is half of the width.
Value : Any relevant value.

Question 18.
Find: [4]

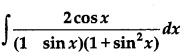
Solution:

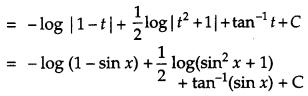
Question 19.
Find the particular solution of the differential equation e^x tan ydx + (2 – ex) sec² ydy = 0, given that y = π4 when x = 0. [4]
Solution:
Given differential equation is,

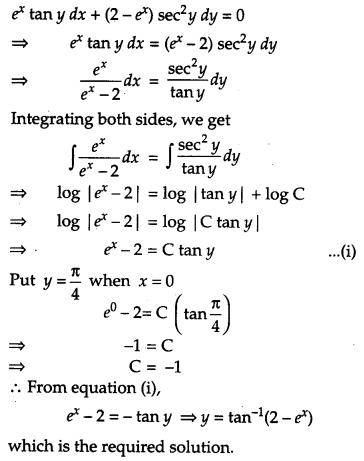
OR
Find the particular solution of the differential equation dydx + 2y tan x = sin x, given than y = 0 when x = π3.
Solution:
Given differential equation is,

Hence, particular solution is
y sec² x = sec x – 2
or y = cos x – 2 cos²x

Question 21.
Find the shortest distance between the lines r⃗ =(4i^−j^)+λ(i^+2j^−3k^) and r⃗ =(i^−j^+2k^)+μ(2i^+4j^−5k^) [4]
Solution:
Given lines are

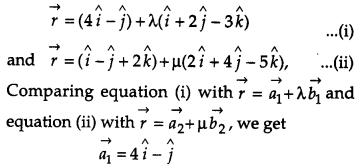
Question 22.
Suppose a girl throws a die. If she gets 1 or 2, she tosses a coin three times and notes the number of tails. If she gets 3, 4, 5 or 6, she tosses a coin once and notes whether a ‘head’ or ‘tail’, is obtained. If she obtained exactly one “tail7, what is the probability that she threw 3, 4, 5 or 6 with the dice? [4]
Solution :
Let E₁ be the event that girl gets 1 or 2 on the roll and E₂ be the event that girl gets 3, 4, 5, or 6 on the roll of a die.

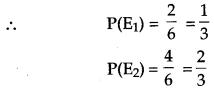
Let A be the event that she gets exactly one tail. If she tossed coin 3 times and gets exactly one tail then possible outcomes are HTH, HHT, THH

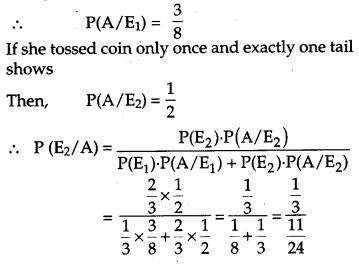
= 811

Question 23.
Two numbers are selected at random (without replacement) from the first five positive integers. Let X denote the larger of the two numbers obtained. Find the mean and variance of X. [4]
Solution:
First five positive integers are 1, 2, 3, 4, 5. We select two positive numbers in 5 × 4 = 20 ways. Out of these, two numbers are selected at random. Let X denote larger of the two selected numbers. Then, X can have values 2, 3, 4 or 5.
P(X = 2) – P (larger no. is 2) = {(1, 2) and (2, 1)}


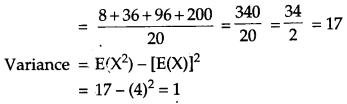
Therefore, mean and variance are 4 and 1 respectively.

Section – D

Question 24.
Let A = {x ϵ Z : 0 ≤ x ≤ 12}. Show that R = {(a, b): a, b ϵ A, | a – b | is divisible by 4} is an equivalence relation. Find the set of all elements related to 1. Also write the equivalence class [2]. [6]
Solution:
Given, R = {(a, b): a, b ϵ A, | a – b | is divisible by 4}
Reflexivity: For any a ϵ A
| a – a | = 0, which is divisible by 4
(a, a) ϵ R
So, R is reflexive.

Symmetry: Let (a, b) ϵ R
⇒ | a – b | is divisible by 4
⇒ | b – a | is divisible by 4 [ ∵ | a – b | = | b – a | ]
⇒ (b, a) ϵ R
So, R is symmetric.

Transitive : Let (a, b) ϵ R and (b, c) ϵ R
⇒ | a – b | is divisible by 4
⇒ | a – b | = 4k
∴ a – b = ± 4k, k ϵ Z …(i)
Also, |b – c| is divisible by 4
⇒ |b – c| = 4m
∴ b – c = ±4m, m ϵ Z …(ii)
Adding equations (i) and (ii)
a – b + b – c = ±4 (k + m)
⇒ a – c = ±4 (k + m)
|a – c | is divisible by 4,
⇒ (a, c) ϵ R
So, R is symmetric.
⇒ R is reflexive, symmetric and transitive.
∴ R is an equivalence relation.
Let x be an element of R such that (x, 1) ϵ R
Then | x – 1| is divisible by 4
x – 1 = 0, 4, 8, 12,
⇒ -x = 1, 5, 9 (∵ x ≤ 12)
∴ Set of all elements of A which are related to 1 are {1, 5, 9}.
Equivalence class of 2 i.e.
[2] = {(a, 2): a ϵ A, |a – 2| is divisible by 4}
⇒ | a – 2| = 4k(k is whole number, k ≤ 3)
⇒ a = 2, 6, 10
Therefore, equivalence class [2] is {2, 6, 10]
OR
Show that the function f : R → R defined by f(x) = xx2+1, ∀x ϵ R is neither one-one nor onto. Also,if g: R → R is defined as g(x) = 2x – 1, find fog(x).
Solution:

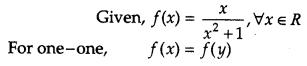
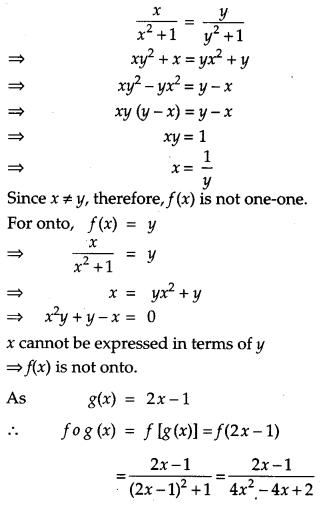
Question 25.
If A = ⎡⎣⎢231−3215−4−2⎤⎦⎥, find A^-1. Use it to solve the system of equation: [6]
2x – 3y + 5z = 11
3x + 2y – 4z = -5
x + y – 2z = -3
Solution:



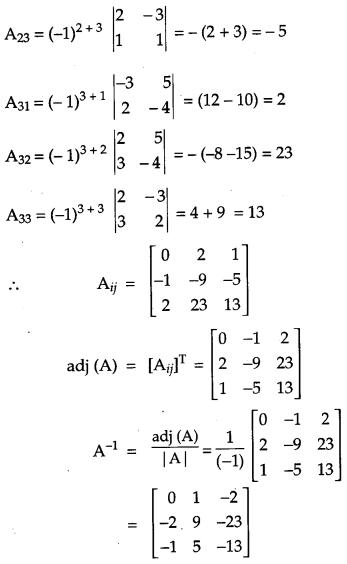
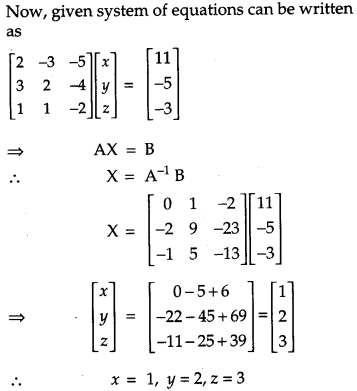
OR
Using elementary row transformations, find the inverse of the matrix:

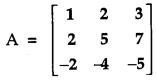
Solution:
We know that, A = IA

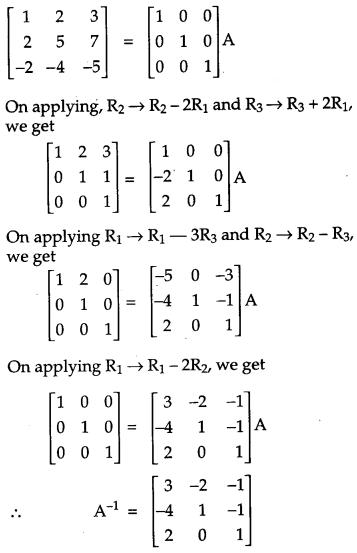
Question 26
Using integration, find the area of the region in the first quadrant enclosed by the X-axis, the line y = x and the circle x² + y²= 32. [6]
Solution:
Given curve is

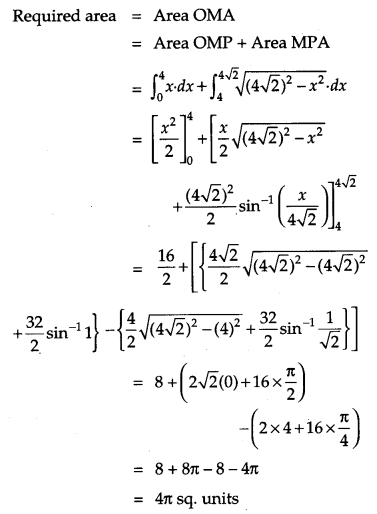
Question 27.
Evaluate: [6]

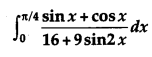
Solution:


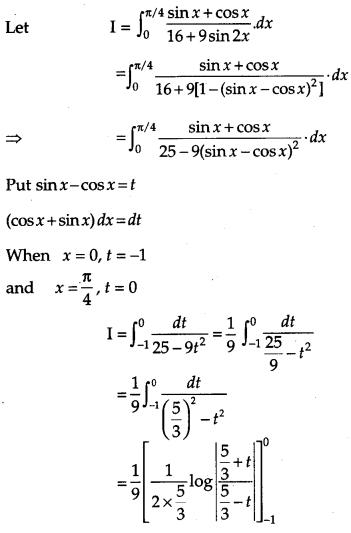
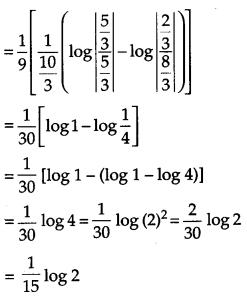
OR
Evaluate ∫31(x2+3x+ex)dx as the limit of the sum.
Solution:

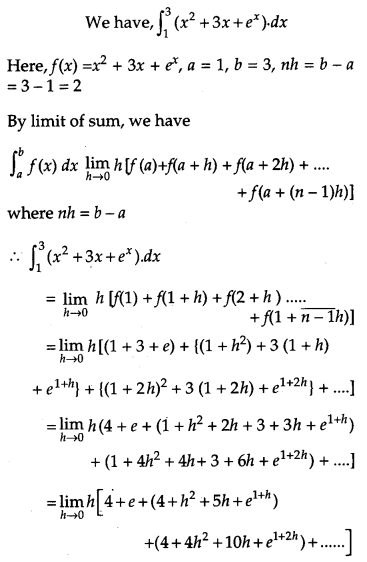
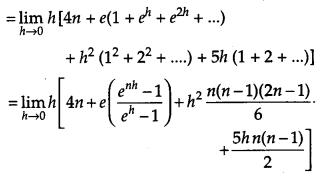
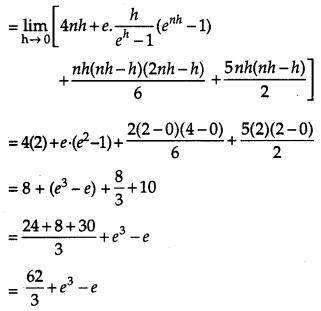
Question 29.
A factory manufactures two types of screws A and B, each type requiring the use of two machines, an automatic and a hand-operated. It takes 4 minutes on the automatic and 6 minutes on the hand-operated machines to manufacture a packet of screws ‘A’ while it takes 6 minutes on the automatic and 3 minutes on the hand- operated machine to manufacture a packet of screws ‘B’. Each machine is available for at most 4 hours on any day. The manufacturer can sell a packet of screws ‘A’ at a profit of 70 paise and screws ‘B’ at a profit of ₹1. Assuming that he can sell all the screws he manufactures, how many packets of each type should the factory owner produce in a day in order to maximize his profit ? Formulate the above LPP and solve it graphically and find the maximum profit [6]
Solution:
Let the number of packets of screw ‘A’ manufactured in a day be x and that of screw B be y.

Plotting the points on the graph, we get the feasible region OABC as shown (Shaded).


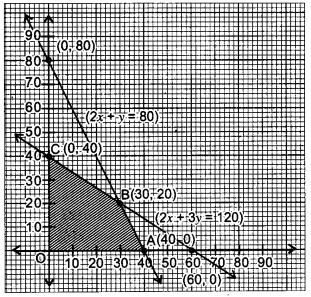
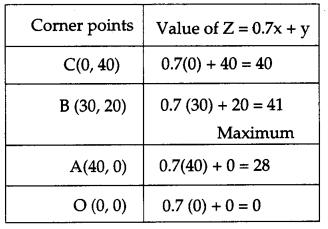
Hence, profit will be maximum if company produces 30 packets of screw A and 20 packets of screw B and maximum profit = ₹ 41.

Class 12 Mathematics Previous Year Question Paper – 2018

Section – A

Question 1.
If x ϵ N and ∣∣∣x+3−3x−22x∣∣∣ = 8, then find the value of x. [1]
Solution:
We have, ∣∣∣x+3−3x−22x∣∣∣ = 8
⇒ (x + 3) × 2x – (-2) × (-3x) = 8
⇒ 2x² + 6x – 6x = 8
⇒ 2x² = 8
⇒ x² = 4
But x ≠ -2 as x ϵ N
⇒ x = 2

Question 2.
Use elementary column operation C₂ → C₂ + 2C₁ in the following matrix equation : [1]

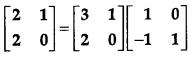
Solution:
We have

Question 3.
Write the number of all possible matrices of order 2 × 2 with each entry 1, 2 or 3. [1]
Solution:
Total number of all possible matrices of order 2 × 2 with each entry 1, 2 or 3 are 3⁴ i.e., 81.

Q. 4 Find the vector equation of the plane with intercepts 3,-4 and 2 on x, y and z-axis respectively. [1]
Solution:
The equation of the required plane is,

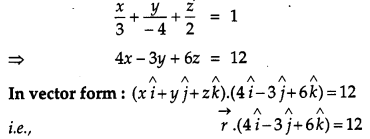
This is the vector equation of the plane with intercept 3,-4 and 2 on coordinate axis.

Section- B

Question 7.
Find the coordinates of the point where the line through the points A(3, 4, 1) and B(5, 1, 6) crosses the XZ-plane. Also find the angle which this line makes with the XZ-plane. [4]
Solution:
The equation of the line passing through A and B is,

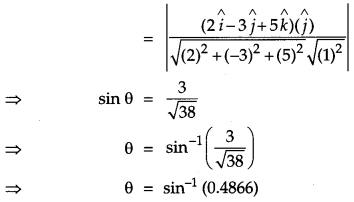
Question 8.
The two adjacent sides of a parallelogram are 2i^−4j^−5k^ and 2i^+2j^+3k^. Find the two unit vectors parallel to its diagonals. Using the diagonal vectors, find the area of the parallelogram. [4]
Solution:
Let ABCD be a parallelogram such that

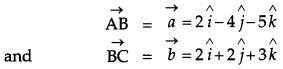
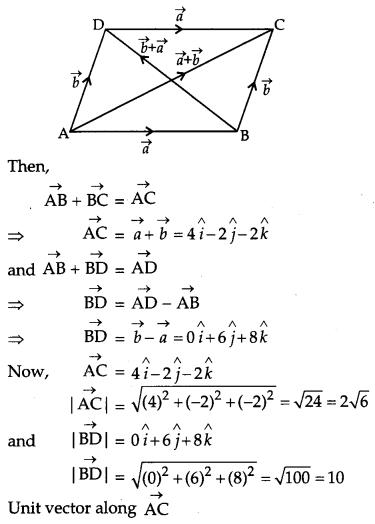
Question 9.
In a game, a man wins ₹ 5 for getting a number greater than 4 and loses ₹ 1 otherwise, when a fair die is thrown. The man decided to throw a die thrice but to quit as and when he gets a number greater than 4. Find the expected value of the amount he wins/loses. [4]
Solution:
Let n denote the number of throws required to get a number greater than 4 and X denote the amount won/lost.
The man may get a number greater than 4 in the very first throw of the die or in second throw or in the third throw.
Let p = Probability of getting a number greater than 4

OR
A bag contains 4 balls. Two balls are drawn at random (without replacement) and are found to be white. What is the probability that all balls in the bag are white ?
Solution:
We know that the number of white balls can’t be less than 2.
Now, there are different cases, for the number of white balls in the bag. The total cases are ²C₂ + ³C₂ + ⁴C₂.

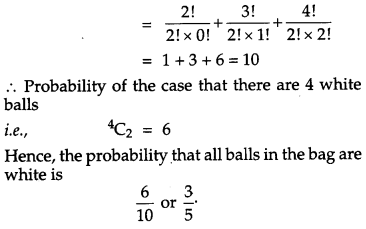
Question 10.
Differentiate x^sinx + (sin x)^cosx with respect to x. [4]
Solution:
We have,

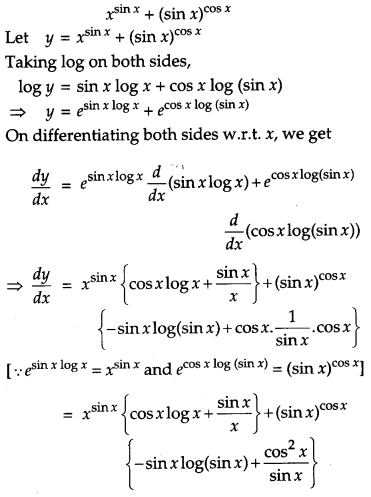
OR
If y = 2 cos(log x) + 3 sin(log x), prove that

Solution:
Given, y = 2 cos (log x) + 3 sin (log x) On differentiating both sides w.r.t. x, we get

Question 11.
If x = a sin 2t (1 + cos 2t) and y = b cos 2t (1 – cos 2t), find dydx at t = π4. [4]
Solution:
We have, x = a sin 2t (1 + cos 2t)

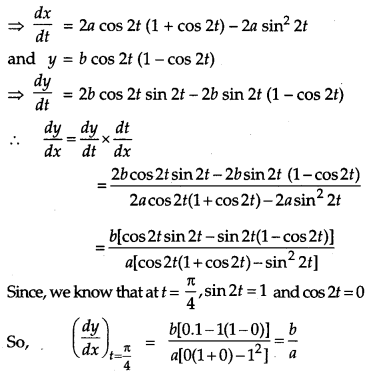
Question 12.
The equation of tangent at (2, 3) on the curve y² = ax³ + b is y = 4x – 5. Find the value of a and b. [4]
Solution:
Since the point (2, 3) lies on the curve y² = ax³ + b

Question 13.
Find: [4]

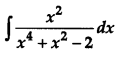
Solution:
Let,

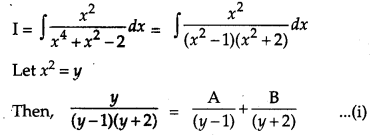
Question 14.
Evaluate: [4]

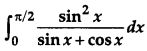
Solution:
We have,


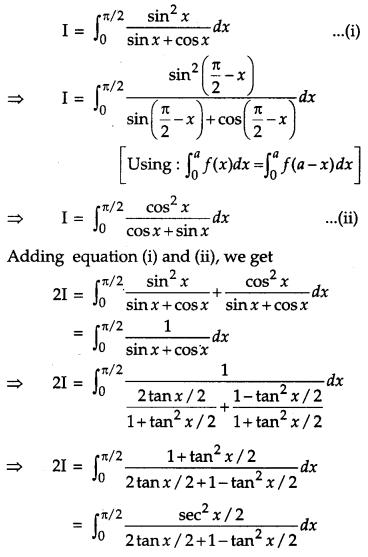
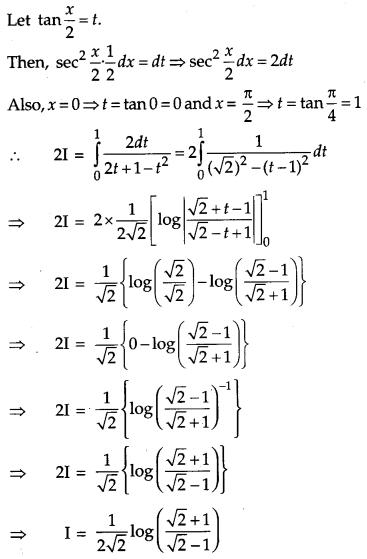
OR
Evaluate:

Solution:

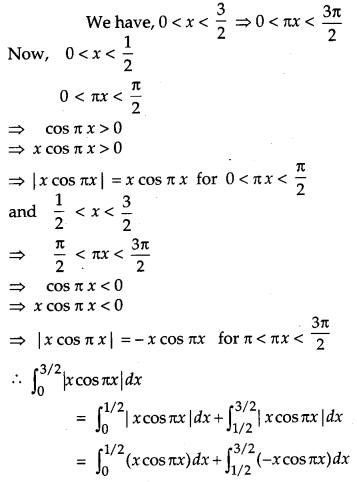
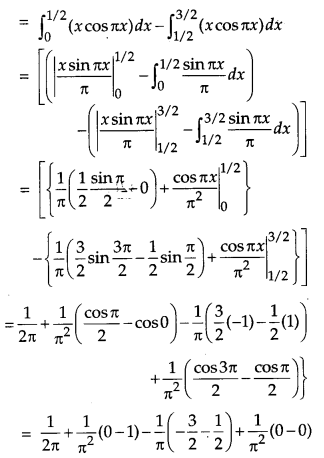
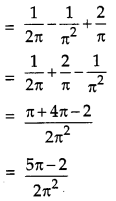
Question 15.
Find: [4]

Solution:

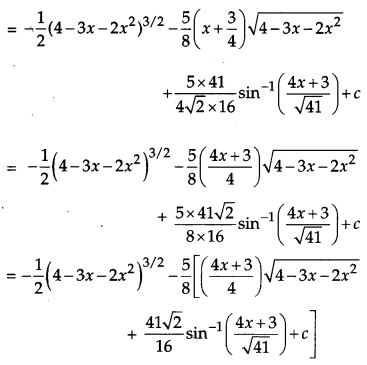
Question 16.
Solve the differential equation: [4]

Solution:

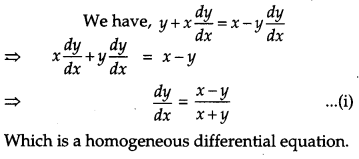
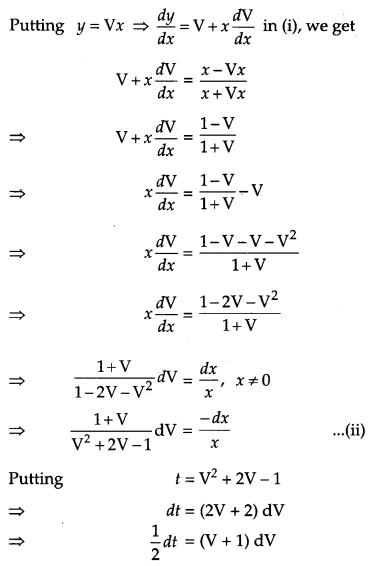
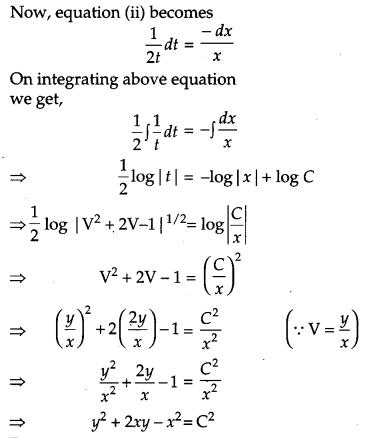
Question 17.
Form the differential equation of the family of circles in the second quadrant and touching the coordinate axes. [4]
Solution:
The equation of circles in the second quadrant which touch the coordinate axes is
(x + a)² + (y – a)² = a², a ϵe R …(i)

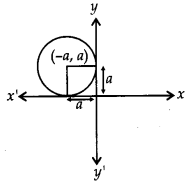
where a is a parameter. This equation contains one arbitrary constant. So we shall differentiate it once only and we shall get a differential equation of first order.
Differentiating (i) w. r. t. x, we get

This is the required differential equation representing the given family of circles.

Question 18.
Solve the equation for x : sin^-1 x + sin^-1 (1 – x) = cos^-1 x. [4]
Solution:


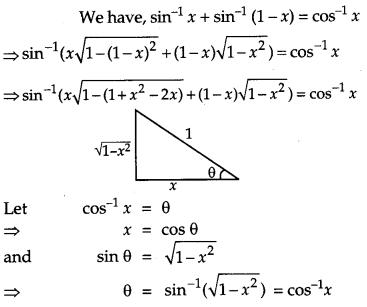
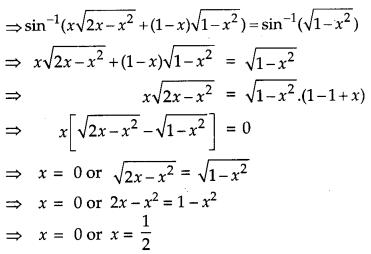
OR

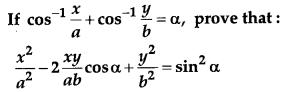
Solution:

Question 19.
A trust invested some money in two types of bond. The first bond pays 10% interest and second bond pays 12% interest. The trust received ₹ 2,800 as interest. However, if trust had interchanged money in bonds, they would have got ₹ 100 less as interest. Using matrix method, find the amount invested by the trust. Interest received on this amount will be given to Helpage India as donation. Which value is reflected in this question ? [4]
Solution:
Let the amount invested by the trust in first and second bond be x and y respectively.

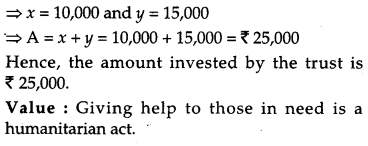
Section – C

Question 20.
There are two types of fertilisers ‘A’ and ‘B’. ‘A’ consists of 12% nitrogen and 5% phosphoric acid whereas ‘B’ consists of 4% nitrogen and 5% phosphoric acid. After testing the soil conditions, farmer finds that he needs at least 12 kg of nitrogen and 12 kg of phosphoric acid for his crops. If ‘A’ costs ₹ 10 per kg and ‘B’ cost ₹ 8 per kg, then graphically determine how much of each type of fertiliser should be used so that nutrient requirements are met at a minimum cost. [6]
Solution:
Let the quantity of fertiliser A and B be x and y respectively.
To minimize : Z = ₹ (10x + 8y)
Subject to the constraints :


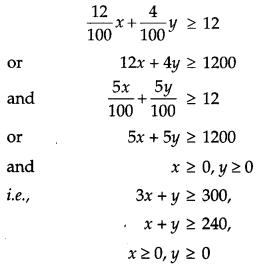
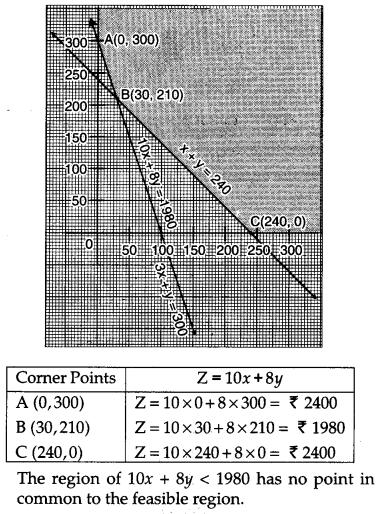
So, Z is minimum for x = 30 and y = 210 and the minimum value of Z is ₹ 1980.
Hence, the quantity of fertilizer A is 30 kg and of fertilizer B is 210 kg.

Question 21.
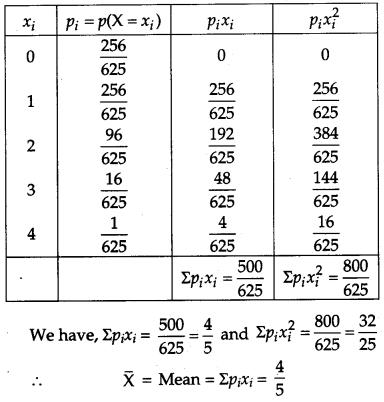
Five bad oranges are accidently mixed with 20 good ones. If four oranges are drawn one by one successively with replacement, then find the probability distribution of number of bad oranges drawn. Hence find the mean and variance of the distribution. [6]
Solution:
Let X denotes the number of bad oranges in a draw of 4 oranges from a group of 20 good oranges and 5 bad oranges. Since there are 5 bad oranges in the group, therefore X can take values, 0, 1, 2, 3, 4.
Now, P(X = 0) = Probability of getting no bad orange.
P(X = 0) = Probability of getting 4 good oranges

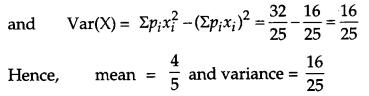
Question 22.
Find the position vector of the foot of perpendicular and the perpendicular distance from the point P with position vector 2i^+3j^+4k^ to the plane r⃗ ⋅(2i^+j^+3k^)−26=0. Also find image of P in the plane. [6]
Solution:
Let L be the foot of the perpendicular

Question 23.
Show that the binary operation * on A = R – {-1} defined as a * b = a + b + ab for all a, b ϵ A is commutative and associative on A. Also find the identity element of * in A and prove that every element of A is invertible.** [6]

Question 24.
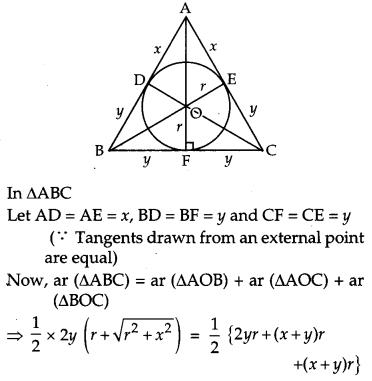
Prove that the least perimeter of an isosceles triangle in which a circle of radius r can be inscribed is 63–√rr. [6]
Solution:
Let ABC be an isosceles triangle with AB = AC and a circle with centre O and radius r, touching sides AB, BC, CA at D, F, E respectively.





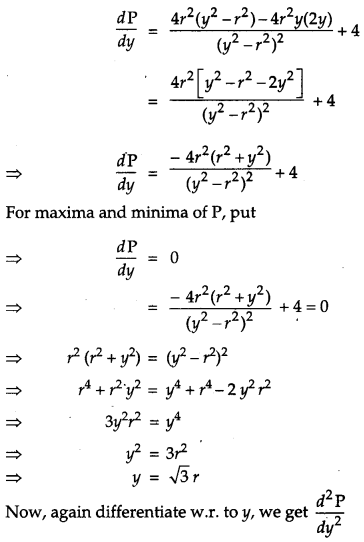
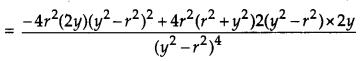
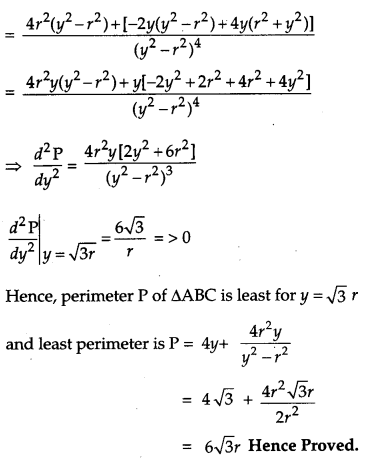
OR
If the sum of lengths of hypotenuse and a side of a right angled triangle is given, show that area of triangle is maximum, when the angle between them is π3.
Solution:
Let ABC be a right angled triangle with base BC = x, AB = y such that x + y = k (constant).
Let A be the angle between base and hypotenuse.
Let A be the area of the tringle. Then,

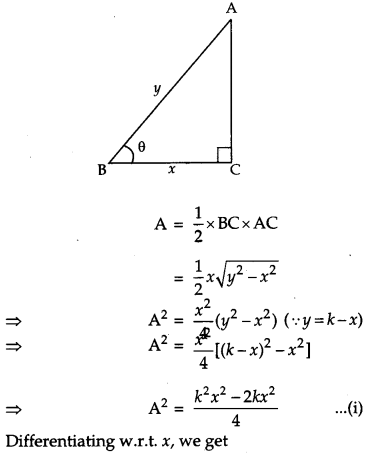
Question 25.
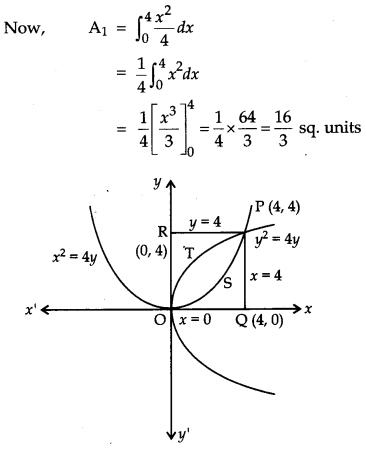
Prove that the curves y² = 4x and x² = 4y divide the area of square bounded by x = 0, x = 4, y = 4 and y = 0 into three equal parts. [6]
Solution:
Let A₁, A₂ and A₃ denote areas OSPQO, OSPTO and OTPRO respectively.
To prove : A₁ = A₂ = A₃,

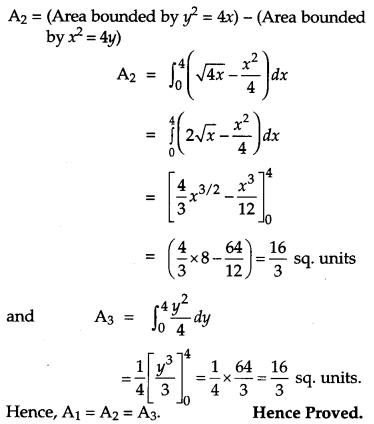
Question 26.
Using properties of determinants, show that ∆ABC is isosceles if: [6]

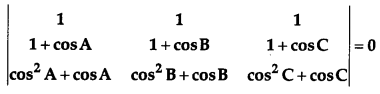
Solution:
We have,

⇒ Expanding along R₁ (cos B – cos A) (cos C – cos A) [1 + cos A + cos C – 1 – cos A – cos B] = 0
⇒ (cos B – cos A) (cos C – cos A) (cos C – cos B) = 0
Either cos B = cos A or cos C = cos A or cos C = cos B
i.e., either BC = AC or BC = AB or AC = AB
Hence, ∆ ABC is isosceles. Hence Proved.
OR
A shopkeeper has 3 varieties of pens ‘A’, ‘B’ and ‘C’. Meenu purchased 1 pen of each variety for a total of ₹ 21. Jeevan purchased 4 pens of ‘A’ variety, 3 pens of ‘B’ variety and 2 pens of ‘C variety for ₹ 60. While Shikha purchased 6 pens of ‘A’ variety, 2 pens of ‘B’ variety and 3 pens of ‘C’ variety for ₹ 70. Using matrix method, find cost of each variety of pen.
Solution:
Let the cost of each variety of pen be ₹ x, ₹ y and ₹ z respectively. Then,
x + y + z = 21
4x + 3y + 2z = 60
and 6x + 2y + 3z = 70
This system of equations can be written in matrix form as follows:




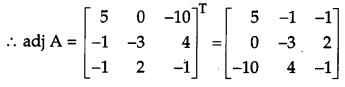
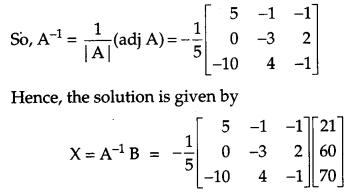
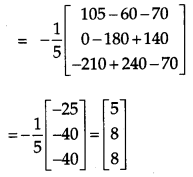
Hence, the cost of each variety of pen are ₹ 5, ₹ 8 and ₹ 8 respectively.

FAQs on Class 12 Mathematics Previous Year Question Papers

Q. Where I can get CBSE Class 12th Mathematics Previous Year Question Papers?

You can get CBSE Class 12 Mathematics Previous Year Question Papers on this page. We have given solved CBSE Class 12 Mathematics Previous Year Question Papers on this page.

Q. Are CBSE Class 12 Mathematics Previous Year Question Papers helpful to get good marks?

Yes, CBSE Class 12 Mathematics Previous Year Question Papers are very helpful to get good marks in the CBSE Term 2 Examination. The students must solve all the CBSE Class 12 Mathematics Previous Year Question Papers to pass CBSE Class 12th Term 2 Exam 2022 with flying colours.

Q. Which website is best for previous year’s question papers of CBSE Class 12th?

The Adda247 School website is best for previous year’s question papers for CBSE Class 12th. Adda247 School has covered the previous year’s question papers of all the subjects of CBSE Class 12th on its official website.

Sharing is caring!