CBSE Class 10 Maths Sample Paper with Solution 2025 PDF: The Central Board of Secondary Education is going to hold the CBSE Class 10 Mathematics board exam on March 10, 2025. Students who are going to appear for this board exam must practice the most expected important questions for the board exam. Solving the most important questions present in the CBSE Class 10 Maths Sample Paper 2024-25 will help students score excellent marks in exam. We are providing the board exam practice questions for Math Standard and Basic subjects here.
CBSE Class 10 Maths Sample Paper 2024-25
The secret to scoring 95+ marks in CBSE Class 10 Maths board paper is to practice questions that have more chances of being asked in the exam. These questions are provided in the sample paper have been formulated by experts who also sit on the board team that are responsible for setting board papers. That is why, students should not ignore these questions. Practicing these questions will definitely increase the conceptual understanding of students and will prepare them effectively for board paper.
Sample Paper Class 10 2024-25 Maths Solutions for Board Exam
Some of the most important and expected CBSE board exam questions from the mathematics standard and mathematics basic subject has been added below.
CBSE Class 10 Maths Sample Paper 2024-25 with Solutions for Board Exam
Q) If the height of the tower is equal to the length of its shadow, then the angle of
elevation of the sun is _____
a) 30° b) 45° c) 60° d) 90°
Q) When a dice is thrown once, the probability of getting an even number less than 4 is
a) 1/4 b) 0 c) 1/2 d) 1/6
Q) The area of the circle is 154cm². The radius of the circle is
a) 7cm b) 14cm c) 3.5cm d) 17.5cm
Q) Assertion (A): The point (0, 4) lies on y-axis.
Reason(R): The x-coordinate of a point on y-axis is zero
(a) Both assertion (A) and reason (R) are true and reason (R) is the correct explanation of assertion (A).
(b) Both assertion (A) and reason (R) are true but reason (R) is not the correct explanation of assertion (A).
(c) Assertions (A) is true but reason (R) is false.
(d) Assertions (A) is false but reason (R) is true.
Q) Find whether the following pair of linear equations is consistent or inconsistent:
3x + 2y = 8
6x – 4y = 9
Q) Prove that √3 is an irrational number.
Q) The coach of a cricket team buys 4 bats and 1 ball for Rs. 2050. Later, she buys 3 bats and 2 balls for 1600. Find the cost of each bat and each ball.
Q) Find the zeroes of the quadratic polynomial 4s²– 4s + 1 and verify the relationship between the zeroes and the coefficients.
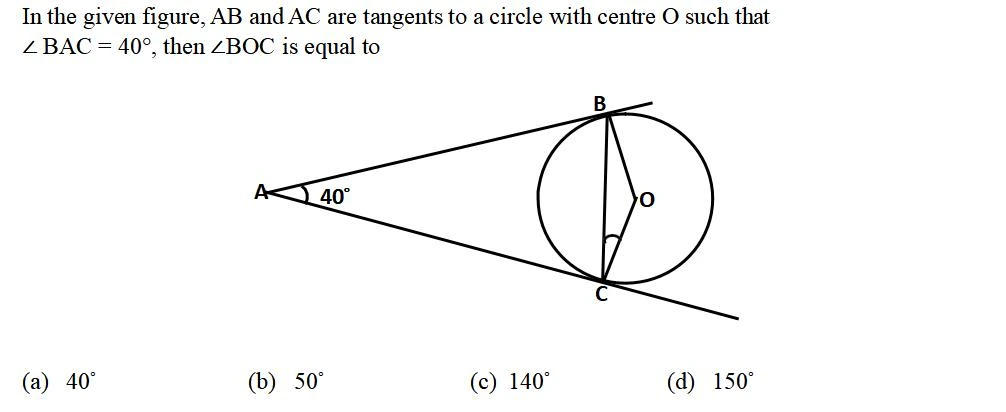
CBSE Sample Paper 2024-25 Class 10 Maths Standard with Solution for Board Exam
Q) The nature of roots of the quadratic equation 9×2 – 6x – 2 = 0 is:
(a) No real roots (b) 2 equal real roots
(c) 2 distinct real roots (d) More than 2 real roots
Q) Two APs have the same common difference. The first term of one of these is –1 and that of the other is – 8. The difference between their 4th terms is
(a) 1 (b) -7 (c) 7 (d) 9
Q) What is the ratio in which the line segment joining (2,-3) and (5, 6) is divided by x-axis?
(a) 1:2 (b) 2:1 (c) 2:5 (d) 5:2
Q) A point (x,y) is at a distance of 5 units from the origin. How many such points lie in the third quadrant?
(a) 0 (b) 1 (c) 2 (d) infinitely many
Q) If a pole 6 m high casts a shadow 2 √3m long on the ground, then the Sun’s elevation is
(a) 60° (b) 45° (c) 30° (d) 90°
Q) If the perimeter and the area of a circle are numerically equal, then the radius of the circle is
(a) 2 units (b) π units (c) 4 units (d) 7 units
Q) It is proposed to build a new circular park equal in area to the sum of areas of two circular parks of diameters 16 m and 12 m in a locality. The radius of the new park is
(a) 10m (b) 15m (c) 20m (d) 24m
Q) The sum of a two digit number and the number obtained by reversing the digits is 66. If the digits of the number differ by 2, find the number. How many such numbers are there?
Sample Paper Class 10 Maths 2024 25 with Solutions by Experts
Students can practice all the important questions for the CBSE Class 10 Mathematics board exam 2025. Make sure to go through the solutions provided for each and every question after solving the individual paper to make your concepts more clear.
CBSE Class 10th Maths Most Repeated Board Exam Questions Chapter-wise
In this section, students can solve the most important questions for board exam from every chapter. Download the chapter-wise important and expected questions for the CBSE Class 10 board exam 2025 below.
| Chapter No. | PDF Download Link |
| Chapter 1 & 2 | Download PDF |
| Chapter 3 & 4 | Download PDF |
CBSE Class 10 Maths Sample Paper with Solution PDF Download
The sample paper with solutions for CBE Class 10th Maths for the 2024-25 academic year, covering both basic and standard courses, is now accessible on the official website at cbseacademic.nic.in. Working on the class 10 maths sample paper with solutions in PDF format will aid students in understanding how to respond to questions within the given time frame. It also boosts their confidence, reduces exam anxiety, and aids them in identifying their improvement areas. To simplify matters, we have included the direct link to download the 2025 PDF sample paper for class 10 math, complete with solutions for both courses.
|
Class 10 CBSE Maths Sample Paper 2024-25 with Solutions PDF
|
||
| Maths Subject | Sample Paper PDF Download | Solutions PDF |
| Maths Sample Paper Class 10 2024-25 Standard | Sample Paper PDF | Marking Scheme & Solutions |
| Maths Sample Paper Class 10 2024-25 Basic | Sample Paper PDF | Marking Scheme with Solutions |
CBSE Maths Class 10 Sample Paper with Solutions: Important Questions
The important questions that have students should practice in the last few days before the board exam has been provided below. These questions have highest chances of being asked in the exam as it has been prepared by top industry experts.
| Question | Options |
| Find the value of k for which the system of equations x + (k + l) y = 5 and (k + l) x + 9 y = 8k – 1 has infinitely many solutions | (a) 2, (b) 3, (c) 4, (d) 5 |
| ∆ABC ~ ∆PQR. If AM and PN are altitude of ∆ABC and ∆PQR respectively and AB² : PQ² = 25 : 36, then AM : PN = ——– | (a) 2 : 5, (b) 5 : 6, (c) 25 : 36, (d) 2 : 3 |
| If the circumference of a circle increases from 2π to 4π, then its area becomes of the original area | (a) half, (b) double, (c) three times, (d) four times |
| P (5,1), Q (1,4) and R (8,5) are the coordinates of the vertices of a triangle. Which of the following types of triangle will ∆PQR be | (a) equilateral triangle, (b) scalene right angled triangle, (c) isosceles right angled triangle, (d) isosceles acute angled triangle |
| A point (x y) is at a distance of 7 units from the origin. How many such points lie in the third quadrant? | (a) 0, (b) 1, (c) 2, (d) Infinitely many |
| If the area of a sector of a circle is 20% of the area of the circle, then the angle at the centre is equal to | (a) 30˚, (b) 36˚, (c) 45˚, (d) 60˚ |
| If –2 and 3 are the zeroes of quadratic polynomial x² + (p + l) x + q, then p and q are —– respectively. | (a) –7, 2, (b) –6, –2, (c) 2, 6, (d) –2, –6 |
| If g – 1, g + 3 and 3g – 1 are in A.P, then find the value of g. | (a) 3, (b) 4, (c) 5, (d) 7 |
| Two right circular cones have their heights in the ratio 1 : 3 and the radii in the ratio 3 : 1. What is the ratio of their volumes ? | (a) 1 : 3, (b) 2: 3, (c) 3 : 1, (d) 9 : 1 |
| Find the 11th term from the end of the given progression 10, 7, 4, ………, –62. | (a) –32, (b) –16, (c) –25, (d) 0 |
| In triangles ABC and DEF, ∠B = ∠E, ∠F = ∠C, and AB = 3DE. Then the two triangles are | (a) congruent but not similar, (b) similar but not congruent, (c) neither congruent nor similar, (d) congruent as well as similar |
| Statement A (Assertion): HCF of 26 and 91 is 13 and the LCM is 182. Statement R (Reason): As HCF(a,b) × (a × b) = LCM(a,b) | (a) Both Assertion (A) and (R) are True and Reason (R) is the correct explanation of Assertion (A), (b) Both Assertion (A) and Reason (R) are True but Reason (R) is not the correct explanation of Assertion (A), (c) Assertion (A) is True but Reason (R) is False, (d) Assertion (A) is False but Reason (R) is True |
| Assertion (A): The mid-point of a line segment divides it in ratio 1 : 1. Reason (R): Three points are collinear if they lie on same straight line. | (a) Both Assertion (A) and (R) are True and Reason (R) is the correct explanation of Assertion (A), (b) Both Assertion (A) and Reason (R) are True but Reason (R) is not the correct explanation of Assertion (A), (c) Assertion (A) is True but Reason (R) is False, (d) Assertion (A) is False but Reason (R) is True |
| What is the HCF of the least prime number and the least composite number | (a) 1, (b) 2, (c) 3, (d) 4 |
| If mode and mean of a data set are given as 8 and 9 respectively, then the median of the data set is | (a) 8.57, (b) 8.67, (c) 8.97, (d) 9.24 |
| If the area of a sector of a circle is 2/20 of the area of the circle, then the angle at the centre is equal to | (a) 30˚, (b) 36˚, (c) 45˚, (d) 60˚ |
 |
|
| Section B | |
| Solve for x and y: 71x + 37y = 253, 37x + 71 y = 287
OR Find value of x and y: 26x + 28y – 269 = 0, 28x + 26y – 271 = 0 |
|
| Volumes of two spheres are in the ratio 27 : 64, then find the ratio of their surface areas. | |
| Prove that the tangents drawn from an external point to a circle are equal in length.
OR Prove that the parallelogram circumscribing a circle is rhombus. |
|
| A cow is tied to a peg at one corner of a rectangular shaped grass field of 20 m long and 16 m wide with a 14 m long rope. Find the area of that part the cow cannot graze. | |
| Find a quadratic polynomial whose zeroes are (3 + √3) and (3 – √3). | |
CBSE Class 10 Maths Sample Paper 2024-25 Marking Scheme
The CBSE Class 10 Maths exam 2025 marking scheme and unit-wise weightage for the 2025 board exam has been provided below. The marking scheme is same for the CBSE Class 10 Maths sample paper and CBSE Class 10 Maths board exam paper. Students need to make sure they prioritize high-weightage topics first in the final minutes before the exam.
|
Units no.
|
Unit Name
|
Marks
|
|
I
|
NUMBER SYSTEMS
|
06
|
|
II
|
ALGEBRA
|
20
|
|
III
|
COORDINATE GEOMETRY
|
06
|
|
IV
|
GEOMETRY
|
15
|
|
V
|
TRIGONOMETRY
|
12
|
|
VI
|
MENSURATION
|
10
|
|
VII
|
STATISTICS & PROBABILITY
|
11
|
|
|
Total
|
80
|
CBSE Class 10 Maths Exam Pattern 2024-25
By working through these papers, students become familiar with the exam layout, types of questions, and grading system, as the sample paper format mirrors the real CBSE Class 10 Maths Question Paper precisely. Take a look at the structure of the CBSE Class 10 Maths Sample Paper for 2024-25 outlined below:
- This question paper comprises 38 questions that are categorized into 5 sections: A, B, C, D, and E.
- In Section A, items 1-18 are multiple choice questions (MCQs), while items 19 and 20 are Assertion-Reason questions worth 1 mark each.
- In Section B, questions 21-25 consist of very short answer (VSA) questions, each worth 02 marks.
- Sorry, but it seems there’s a misunderstanding; there’s no text provided for paraphrasing. Could you please share the text you want me to paraphrase?
- In Section C, Questions 26-31 are short answer (SA) questions, each worth 03 marks.
- In Section D, Questions 32-35 are long answer (LA) questions, each worth 05 marks.
- In Section E, Questions 36-38 are based on a case study and each is worth 4 marks.
- Subsections of the values of 1, 1, and 2 marks each correspondingly.
- All questions must be answered. Nevertheless, an internal selection of 2 Questions from Section B, 2 Questions from Section C, and 2 Questions from Section D has been included. An internal option has been included in all the 2-mark questions of Section E.
Last Years Class 10 Maths Sample Papers with Solution PDF
Along with the current sample paper, students should also pay focus on questions from the previous year papers. It will help them understand the concept in a more concise and crystal clear manner. Download the CBSE Class 10 Maths sample papers
|
Previous Year’s Class 10 Maths Sample Paper PDF with Solution
|
|||
| Year | Subject | Sample Question Paper | Solution PDF |
| 2023-24 | Mathematics (Basic) | Click Here | Click Here |
| Mathematics (Standard) | Click Here | Click Here | |
| 2022-23 | Mathematics (Basic) | Click Here | Click Here |
| Mathematics (Standard) | Click Here | Click Here | |
| 2021-22 (Term A) | Mathematics (Basic) | Click Here | Click Here |
| Mathematics (Standard) | Click Here | Click Here | |
| 2021-22 (Term B) | Mathematics (Basic) | Click Here | Click Here |
| Mathematics (Standard) | Click Here | Click Here | |
| 2020-21 | Mathematics (Basic) | Click Here | Click Here |
| Mathematics (Standard) | Click Here | Click Here | |
| 2019-20 | Mathematics (Basic) | Click Here | Click Here |
| Mathematics (Standard) | Click Here | Click Here | |
| 2018-19 | Maths | Click Here | Click Here |
| 2017-18 | Maths | Click Here | Click Here |
| 2016-17 | Maths | Click Here | |
| 2015-16 | Maths | Click Here | |
Importance of CBSE Class 10 Maths Sample Paper 2025
Solving the most recent sample paper of Class 10 Maths exam 2025 will provide the following benefits:
1. Familiarity with the Exam Pattern and Marking Scheme
Understanding the exam format and grading criteria is crucial for successful preparation. Sample papers are created to resemble the real exam. They consist of multiple sections and various question formats-like multiple-choice questions (MCQs), brief answers, and extended responses—and show the distribution of marks.
2. Self-Evaluation and Recognizing Knowledge Gaps
Finishing sample papers allows students to evaluate their understanding. It aids them in identifying their strengths and weaknesses across various subjects. This insight enables them to concentrate on aspects requiring enhancement, leading to improved overall readiness. By comparing their responses to the answer keys, students can discover the proper techniques for answering questions. They can also recognize typical errors to stay away of moving forward.
3. Efficient Time Management Practices
Solving the CBSE Class 10 Maths sample papers under timed conditions helps improve time management skills. By learning to manage their time well, students can make the most of the time they have during the exam. As students simulate the exam conditions, they learn to give priority to questions based on how complex they are. This approach teaches students which questions to solve first and how much time to spend on each one.
4. Boosts Self Confidence for the Exam
Successfully practicing the sample papers boosts confidence of students that they can too solve the paper. With practice, students become more comfortable with the exam process, which helps reduce exam stress.
This confidence creates a positive mindset, important for doing well under pressure. Feeling prepared translates into better focus and improved memory recall during the actual exam, which can lead to higher scores. This assurance fosters a constructive attitude, essential for performing effectively under stress. A sense of readiness results in enhanced concentration and improved memory retrieval during the exam, potentially leading to better scores.
CBSE Class 10 Maths Exam Preparation Tips 2025
Students can effectively score 95+ marks in CBSE Class 10 mathematics exam by following the tips shred by experts below.
- Students should initially become acquainted with the syllabus to grasp which topics hold greater importance. Make sure you study based on the most recent syllabus exclusively.
- Mathematics is a discipline that requires consistent practice. It is essential for students to practice as often as possible. Review the questions provided at the conclusion of every chapter.
- Students allocate time to various topics according to their strengths and weaknesses. Avoid allowing your preference for your favorite chapter to influence the schedule. Set aside time for review.
- Work on the problems from the CBSE Class 12 subject textbook to clarify the concepts and enhance comprehension. When tackling problems, students ought to consistently display their rough work clearly, as this will also aid them during exams.
- Attempt several past year question papers and take mock tests to understand the types and difficulty levels of the questions. Addressing these will aid in boosting students’ speed to assess your readiness level. Notice the inquiries that are frequently posed each year.
| Class 10 Sample Papers | |
| Class 10 English Sample Paper 2024-25 | Class 10 Science Sample Paper 2024-25 |
| Class 10 Hindi Sample Paper 2024-25 PDF | Class 10 SST Sample Paper 2024-25 PDF |









 CBSE Class 12 Psychology Question Paper ...
CBSE Class 12 Psychology Question Paper ...
 CBSE Sample Paper 2024-25 Class 10 with ...
CBSE Sample Paper 2024-25 Class 10 with ...
 CBSE Class 12 Biology Question Paper 202...
CBSE Class 12 Biology Question Paper 202...









