Two batteries $$\text{E}_1$$​ (emf: 6V, internal resistance: 0.5 Ω) and $$\text{E}_2$$​ (emf: 12V, internal resistance: 1.0 Ω) are connected in parallel by connecting their positive terminals to point A and negative terminals to point B. A third battery $$\text{E}_3$$​ [emf: 6V, internal resistance: ($$\frac{2}{3}$$​) Ω] is connected in series with this combination by connecting its positive terminal to B. The equivalent emf of this combination is

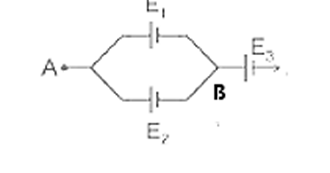
Correct option is D

​$$\text{Given:} \\\text{Battery } E_1 = 6 \ \text{V}, r_1 = 0.5 \ \Omega \\\text{Battery } E_2 = 12 \ \text{V}, r_2 = 1 \ \Omega \\\text{Battery } E_3 = 6 \ \text{V}, r_3 = \frac{2}{3} \ \Omega$$

$$E_1 \text{ and } E_2 \text{ are parallel connection}\text{Then,} \\$$

$$\frac{1}{r_{\text{eq}}} = \frac{1}{r_1} + \frac{1}{r_2}$$

$$\frac{1}{r_{\text{eq}}} = \frac{1}{0.5} + \frac{1}{1} = 3 \ \Omega$$

$$\text{Now } E_{\text{eq}} = r_{\text{eq}} \left( \frac{E_1}{r_1} + \frac{E_2}{r_2} \right)$$

$$E_{\text{eq}} = \frac{1}{3} \left( \frac{6}{0.5} + \frac{12}{1} \right) = 8 \ \text{V}$$

$$\text{Now, the third battery is connected in series with the combination, then} \\E_{\text{eq}} = E_{\text{eq}} + E_3 = 8 + 6 = 14 \ \text{V}$$​​​​​​​​