Compound Interest Formula, Definition, Examples, Questions

Compound interest refers to interest that is computed on both the principal amount and the accumulated interest over a specified duration. The interest gained on a principal during a specific duration is added to the principal, creating a new principal amount for the subsequent time period. Once more, the interest for the subsequent period is computed on the accumulated principal amount. Candidates can learn the Compound Interest Formula for different time period by going through this post.

Compound Interest

Compound interest is the technique for calculating interest that is used in all financial and business dealings globally. The strength of compounding lies in its ability to always be greater than or equal to alternative methods such as simple interest. In contrast to simple interest, which does not compound since past interest is not added to the principal for the current period, compound interest allows interest to build over time. In Compound Interest, the interest per period multiplied by the number of periods in a year yields the simple annual interest rate. The nominal interest rate is another name for the simple annual interest rate.

Compound Interest Definition

Compound interest, also known as interest on principal and interest, is the practice of adding interest to the principal amount of a loan or deposit. Compound interest occurs when interest is reinvested, or added to the loaned capital rather than paid out, or when the borrower is required to pay it, so that interest is earned the following period on the principal amount plus any accumulated interest. In finance and economics, compound interest is common.

The Compound Interest is given by:

Compound Interest = Amount – Principal

Compound Interest Formula

The compound interest formula is a powerful concept in mathematics and commerce, and it is the interest calculated on the initial principal and also on the accumulated interest of previous periods. This results in exponential growth of the investment or debt over time. The formula for calculating compound interest is:

A = P * (1 + r/n)^(n*t)

Where: A = the future value of the investment/loan, including interest P = the principal amount (the initial amount of money) r = the annual interest rate (expressed as a decimal) n = the number of times that interest is compounded per year t = the number of years the money is invested or borrowed for

Let’s break down the compound interest formula step by step:

1. P * r/n: This calculates the amount of interest accrued in one compounding period (usually a year) on the principal P. The rate is divided by n since interest is compounded n times per year.
2. (1 + r/n)^(nt): This term represents the growth factor of the investment due to compounding. It is calculated by adding 1 to the interest rate (expressed as a decimal) per compounding period (r/n) and raising it to the power of (nt), which represents the total number of compounding periods over the investment’s duration.
3. A = P * (1 + r/n)^(n*t): Finally, to get the future value A, we multiply the principal P by the growth factor calculated in the previous step.

It’s essential to use consistent units for the time when using this formula. For example, if the interest rate is an annual rate, then time t should be in years, and n should be the number of times the interest is compounded in one year (e.g., n = 12 for monthly compounding, n = 4 for quarterly compounding).

Let’s look at an example to illustrate how the compound interest formula works:

Example: Suppose you invest Rs.5,000 in a savings account with an annual interest rate of 5%, compounded monthly (n = 12), and you plan to keep the money invested for 3 years (t = 3).

Using the compound interest formula:

A = 5000 * (1 + 0.05/12)^(12*3)

A = 5000 * (1.0041667)^(36)

A ≈ 5000 * 1.1653212

A ≈ RS.5,826.61

After 3 years, your investment would grow to approximately Rs.5,826.61 with compound interest.

Compound interest is a critical concept to understand when dealing with investments, loans, mortgages, or any financial instruments that involve interest payments over time. It allows your money to grow faster compared to simple interest, where interest is only calculated on the initial principal.

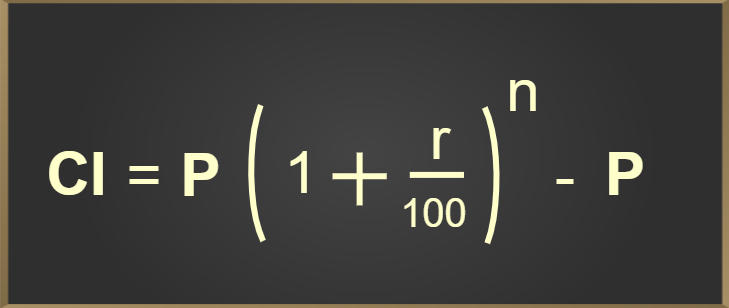
Here,

• CI = Compound Interest
• P = Principal
• r = rate of interest
• n = number of years (‘nt’ if interest is applied t number of times in a year)

Compound Interest Formula in Maths

The total amount of Compound Interest can be calculated by using the following formula for a Periodic Compounding of Compound Interest. The Total amount, which includes the principal sum P and compounded interest I, is calculated by the formula:

where:

• A is the total accumulated amount
• P is the initial principal sum
• r is the interest of the periodic Compound Interest
• n is the annual frequency if compounding of the Compound Interest
• t is the overall length of time for which the compound interest is applied

Compound Interest Formula for Different Time Periods

To calculate the compound interest for another time period, you can modify the values of n and t as needed. The CI formulas are listed in the subsequent table for various time intervals. In each of these equations, P denotes the principal sum, r represents the rate/100, and t indicates the number of years.

Compound Interest Formula Examples

• Example 1: Both compound interest and simple interest predict that if you put 1,000 rupees in an account that offers 1% yearly interest, you would receive 10 rupees in interest after a year. However, thanks to compound interest, you will receive 10.10 rupees in interest payments in Year Two, or 1% interest on a sum of 1,010 rupees (principal plus interest).
• Example 2: Both corporate and governmental bond interest is typically due twice a year. The stated interest rate is divided by two, the principle is multiplied, and the result is the amount of interest paid (every six months). The disclosed rate is lower than the annual compounded rate.
• Example 3: When valuing derivatives, for instance, continuous compounding, which is the maximum as the compounding period approaches 0, is sometimes theoretically simpler. Continuous compounding of these instruments’ prices is an inevitable result of Ito calculus

Compound Interest Formula Questions and Answers

Ques. Find the compound interest (CI) on Rs. 10,000 for 2 years at 15% per annum compounded annually.

Solution:

Given,

Principal (P) = Rs. 10,000

Rate (R) = 15

Number of years (n) = 2

A = P[1 +(R/100)]ⁿ

= 10000[1 + (15/100)]²

= 1000[(100 + 15)/100)]²

= 10000 [(115)/100]²

= 10000 × 1.15²

= 10000 × 1.3225

= 13225

Total amount, A = Rs. 13,225

Compound interest (CI) = A – P

= Rs. 13,225 – Rs. 10,000

Ques. Find the compound interest (CI) on Rs. 10,000 for 2 years at 25% per annum compounded annually.

Solution:

Given,

Principal (P) = Rs. 10,000

Rate (R) = 15

Number of years (n) = 2

A = P[1 +(R/100)]ⁿ

= 10000[1 + (25/100)]²

= 1000[(100 + 25)/100)]²

= 10000 [(125)/100]²

= 10000 × 1.25²

= 10000 × 1.5625

= 15625

Total amount, A = Rs. 15,625

Compound interest (CI) = A – P

= Rs. 15,625 – Rs. 10,000

Sharing is caring!