Correct option is A
Use the identity sin 3 θ = sin θ ( 1 − cos 2 θ ) ∫ sin 3 θ d θ = ∫ sin θ ( 1 − cos 2 θ ) d θ Let u = cos θ , d u = − sin θ d θ ∫ sin θ ( 1 − cos 2 θ ) d θ = ∫ ( 1 − u 2 ) d u = ∫ ( u 2 − 1 ) d u = u 3 3 − u + C Back-substitute u = cos θ cos 3 θ 3 − cos θ + C Evaluate from 0 to π 4 [ cos 3 θ 3 − cos θ ] 0 π 4 = ( cos 3 ( π 4 ) 3 − cos ( π 4 ) ) − ( cos 3 0 3 − cos 0 ) = ( ( 2 2 ) 3 3 − 2 2 ) − ( 1 3 3 − 1 ) = ( 2 3 3 ⋅ 2 3 − 2 2 ) − ( 1 3 − 1 ) = 2 12 − 2 2 + 2 3 = − 5 2 12 + 2 3 = 2 3 − 5 6 2 \textbf{Use the identity } \sin^3 \theta = \sin \theta(1 - \cos^2 \theta) \\\int \sin^3 \theta \, d\theta = \int \sin \theta(1 - \cos^2 \theta) \, d\theta \\\textbf{Let } u = \cos \theta, \, du = - \sin \theta \, d\theta \\\int \sin \theta(1 - \cos^2 \theta) \, d\theta = \int (1 - u^2) \, du = \int (u^2 - 1) \, du = \frac{u^3}{3} - u + C \\\textbf{Back-substitute } u = \cos \theta \\\frac{\cos^3 \theta}{3} - \cos \theta + C \\\textbf{Evaluate from 0 to } \frac{\pi}{4} \\\left[ \frac{\cos^3 \theta}{3} - \cos \theta \right]_0^{\frac{\pi}{4}} = \left( \frac{\cos^3 \left( \frac{\pi}{4} \right)}{3} - \cos \left( \frac{\pi}{4} \right) \right) - \left( \frac{\cos^3 0}{3} - \cos 0 \right) \\= \left( \frac{\left( \frac{\sqrt{2}}{2} \right)^3}{3} - \frac{\sqrt{2}}{2} \right) - \left( \frac{1^3}{3} - 1 \right) \\= \left( \frac{\sqrt{2}^3}{3 \cdot 2^3} - \frac{\sqrt{2}}{2} \right) - \left( \frac{1}{3} - 1 \right) \\= \frac{\sqrt{2}}{12} - \frac{\sqrt{2}}{2} + \frac{2}{3} \\= \frac{-5\sqrt{2}}{12} + \frac{2}{3} \\ = \frac{2}{3} - \frac{5}{6\sqrt2} Use the identity sin 3 θ = sin θ ( 1 − cos 2 θ ) ∫ sin 3 θ d θ = ∫ sin θ ( 1 − cos 2 θ ) d θ Let u = cos θ , d u = − sin θ d θ ∫ sin θ ( 1 − cos 2 θ ) d θ = ∫ ( 1 − u 2 ) d u = ∫ ( u 2 − 1 ) d u = 3 u 3 − u + C Back-substitute u = cos θ 3 cos 3 θ − cos θ + C Evaluate from 0 to 4 π [ 3 cos 3 θ − cos θ ] 0 4 π = ( 3 cos 3 ( 4 π ) − cos ( 4 π ) ) − ( 3 cos 3 0 − cos 0 ) = 3 ( 2 2 ) 3 − 2 2 − ( 3 1 3 − 1 ) = ( 3 ⋅ 2 3 2 3 − 2 2 ) − ( 3 1 − 1 ) = 12 2 − 2 2 + 3 2 = 12 − 5 2 + 3 2 = 3 2 − 6 2 5





 English
English 80 Questions
80 Questions 60 Mins
60 Mins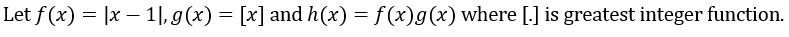
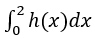 equal to?
equal to?
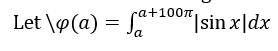
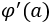 equal to?
equal to?
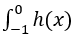 equal to?
equal to?
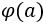 equal to?
equal to?




