Correct option is C
Solution:
We want to evaluate:∫0∞e−x2dx Let I=∫−∞∞e−x2dx Then I2=(∫−∞∞e−x2dx)2=∫−∞∞∫−∞∞e−(x2+y2)dxdy Switching to polar coordinates: x=rcosθ,y=rsinθI2=∫02π∫0∞e−r2⋅rdrdθ=(∫02πdθ)(∫0∞re−r2dr) =2π⋅(21)=π=>I=π Hence, ∫0∞e−x2dx=21∫−∞∞e−x2dx=2π
2π=4π





 English
English 150 Questions
150 Questions 150 Mins
150 Mins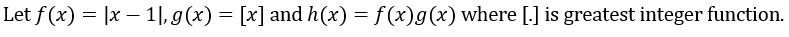
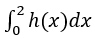 equal to?
equal to?
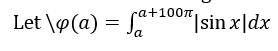
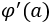 equal to?
equal to?
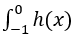 equal to?
equal to?
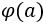 equal to?
equal to?




