Correct option is B
For improper integrals with discontinuities, we must split the integral at the point of discontinuity and take limits:∫−13x21dx=∫−10x21dx+∫03x21dxEvaluate each part separately using limits:1. For ∫−10x21dx:a→0−lim∫−1ax21dx=a→0−lim[−x1]−1a=a→0−lim(−a1+1)=+∞2. For ∫03x21dx:b→0+lim∫b3x21dx=b→0+lim[−x1]b3=b→0+lim(−31+b1)=+∞Both parts diverge to +∞, so the original integral does not converge.ConclusionThe error in the original calculation is that it ignores the discontinuity at x=0.The integral is improper and diverges (i.e., it does not exist as a finite value).The calculation is incorrect because the integral ∫−13x21dx is improper (due to the discontinuity at x=0) and diverges.The correct evaluation shows that the integral does not converge to −34 or any finite value.The integral diverges because x21 is undefined at x=0 and the limits approach +∞.






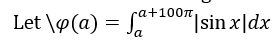
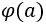 equal to?
equal to?
