Table of Contents
लसावि आणि मसावि (LCM & HCF)
आपण कधी विचार केला आहे का की संख्या आपल्या जगात लपलेले नमुने अनलॉक करणारे आकर्षक रहस्य कसे ठेवू शकतात? आम्ही गणितातील दोन मूलभूत संकल्पना एक्सप्लोर करत असताना आमच्याशी एक आकर्षक प्रवासात सामील व्हा: लघुतम सामाईक विभाज्य (लसावि) [Least common multiple (LCM)] आणि [महत्तम सामाईक विभाजक (मसावि) Highest Common Factor (HCF)], ज्यांना GCD (ग्रेटेस्ट कॉमन डिव्हिजर) असेही म्हणतात. आगामी स्पर्धा परीक्षा जसे की, तलाठी भरती, पोलीस भरती, महानगरपालिका भरती, नगर परिषद भरती, MPSC इत्यादी साठी हा एक महत्वाचा टॉपिक आहे. लसावि आणि मसावि (LCM and HCF) या ब्लॉगमध्ये, तुमची गणितीय पार्श्वभूमी काहीही असो, LCM आणि HCF यांना सर्व जिज्ञासूंसाठी प्रवेश करण्यायोग्य बनवण्याचा आमचा हेतू आहे. तुमची समज दृढ करण्यासाठी अंतर्ज्ञानी स्पष्टीकरणे आणि वास्तविक जीवनातील उदाहरणे प्रदान करून आम्ही तुम्हाला मूलभूत संकल्पनांमधून चरण-दर-चरण घेऊन जाऊ.
लसावि आणि मसावि: विहंगावलोकन
स्पर्धा परीक्षेत बरेच प्रश्न आपल्याला काढून त्याचे उत्तर काढावे लागतात त्यामुळे हा विषय अतिशय महत्वाचा आहे. खालील तक्त्यात आम्ही विहंगावलोकन बद्दल दिले आहे.
| लसावि आणि मसावि: विहंगावलोकन | |
| श्रेणी | अभ्यास साहित्य |
| उपयोगिता | स्पर्धा परीक्षांसाठी |
| विषय | अंकगणित |
| टॉपिकचे नाव | लसावि आणि मसावि |
| लेखातील प्रमुख मुद्दे |
|
लसावि आणि मसावि (LCM & HCF), संकल्पना
- लघुतम सामाईक विभाज्य (लसावि) [Least common multiple (LCM)]
दोन किंवा अधिक संख्यांचा LCM (लसावि) हा सर्वात लहान धन पूर्णांक आहे जो त्या प्रत्येक संख्येने बाकी न उरता भाग जातो. दुसऱ्या शब्दांत, दिलेल्या संख्यांचा लसावि म्हणजे त्यांपैकी प्रत्येक संख्येने विभाज्य अशी लहानांत लहान संख्या असते.
- महत्तम सामाईक विभाजक (मसावि) [Highest Common Factor (HCF)]
दोन किंवा अधिक संख्यांचा HCF किंवा GCD हा सर्वात मोठा धन पूर्णांक आहे जो प्रत्येक संख्येला उर्वरित न ठेवता विभाजित करतो. हे दिलेल्या संख्यांच्या संचाद्वारे सामायिक केलेला सर्वोच्च सामान्य घटक दर्शवतो. म्हणजेच दिलेल्या संख्यांचा HCF (मसावि) म्हणजे त्या संख्यांचा सर्वांत मोठा सामाईक विभाजक असतो.
काही महत्त्वाच्या संज्ञांची संकल्पना
सहमूळ संख्या (Coprime numbers): ज्या दोन संख्यांचा सामाईक विभाजक फक्त 1 हाच असतो, त्या संख्या एकमेकींच्या सहमूळ संख्या आहेत असे म्हणतात. सहमूळ संख्यांना सापेक्ष मूळ संख्या (relatively prime numbers) असेही म्हणतात.
जसे : 10 व 21 या संख्या सहमूळ संख्या आहेत. कारण 10 चे विभाजक : 1, 2, 5, 10 आणि 21 चे विभाजक 1, 3, 7, 21. या दोनही संख्यांच्या विभाजकांमध्ये 1 हा एकमेव सामाईक विभाजक आहे. (3, 8) ; (4, 9); (21, 22) ; (22, 23) ; (23, 24) या काही सहमूळ संख्या आहेत.
जाेडमूळ संख्या (Twin prime numbers): ज्या दोन मूळ संख्यांतील फरक 2 आहे, त्या दोन मूळ संख्यांना जोडमूळ संख्या असे म्हणतात. जसे : (3, 5) ; (5, 7) ; (11, 13) ; (29, 31) इत्यादी.
संख्येचे अवयव (Factors): संख्यांना दिलेल्या संख्येचे अवयव असे म्हटले जाते जेव्हा ते त्या संख्येला अचूकपणे विभाजित करतात. अशा प्रकारे, 18 चे अवयव 1, 2, 3, 6, 9 आणि 18 आहेत.
सामाईक अवयव (Common Factor): दोन किंवा अधिक संख्यांचा सामाईक अवयव ही संख्या असते जी त्या प्रत्येकाला तंतोतंत विभाजित करते. अशा प्रकारे, 2, 4 आणि 8 हे 8 आणि 24 चे सामाईक अवयव आहेत.
गुणाकार (Multiple): जेव्हा एखादी संख्या दुसर्या संख्येने पूर्ण भाग जाते, तेव्हा पूर्वीच्या संख्येला नंतरच्या संख्येचा गुणाकार म्हणतात. अशा प्रकारे, 45 हा 1, 3, 5, 9, 15 आणि 45 चा गुणाकार आहे.
सामाईक गुणाकार (Common Multiple): दोन किंवा अधिक संख्यांचा सामाईक गुणाकार ही अशी संख्या असते जी त्यांपैकी प्रत्येकाने पूर्णतः भागता येते. उदाहरणार्थ, 12, 24 आणि 36 हा 3, 4, 6 आणि 12 चा सामाईक गुणाकार आहे.
संख्येचे मूळ अवयव पाडणे (Prime factorisation of a number): दिलेली संख्या तिच्या मूळ अवयवांच्या गुणाकाराच्या रूपात लिहिणे म्हणजे त्या संख्येचे मूळ अवयव पाडणे होय. संख्यांचा लसावि व मसावि काढण्यासाठी युक्लिडचा एक सोपा व महत्त्वाचा नियम अनेकदा वापरला जातो. “कोणतीही संयुक्त संख्या ही मूळ संख्यांच्या गुणाकाराच्या रूपात लिहिता येते” हा तो नियम आहे.
लसावि आणि मसावि कसे काढायचे?
दिलेल्या संख्येच्या संचाचा मसावि (HCF) शोधण्याच्या पद्धती खालीलप्रमाणे आहेत:
1.मूळ अवयव पाडून संख्यांचा मसावि काढणे (प्राइम फॅक्टरायझेशन पद्धत)
दिलेल्या प्रत्येक संख्याला मूळ अवयवांचे गुणाकार म्हणून व्यक्त करा. सामाईक मूळ अवयवांचा कमीत कमी घातांक/घात चा गुणाकार मसावि (HCF) देते.
मूळ अवयव पाडून (प्राइम फॅक्टरायझेशन पद्धतीने) 8 आणि 14 चा HCF शोधा?
उत्तर: 8 = 2 x 2 x 2, 14 = 2 x 7, 8 आणि 14 चा सामाईक मूळ अवयव 2 आहे त्यामुळे, 8 आणि 14 चा चा महत्तम सामाईक विभाजक (HCF) 2 आहे.
2. मसावि काढण्याची भागाकार पद्धत (Successive Division method):
(1) मोठ्या संख्येला लहान संख्येने भागा.
(2) या भागाकारात मिळणाऱ्या बाकीने आधीच्या भाजकाला भागा.
(3) पायरी 2 मध्ये भागाकाराने मिळणाऱ्या बाकीने पायरी 2 मधील भाजकाला भागा व बाकी काढा.
(4) याप्रमाणे बाकी शून्य मिळेपर्यंत क्रिया करा.
ज्या भागाकारात बाकी शून्य मिळाली त्या भागाकारातील भाजक हा आधी दिलेल्या संख्यांचा मसावि आहे.
उदा: 144 आणि 252 चा मसावि काढा.
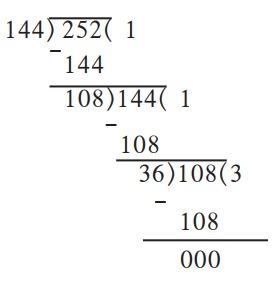
∴ 144 व 252 यांचा मसावि = 36
दिलेल्या संख्येच्या संचाचा लसावि (LCM) शोधण्याच्या पद्धती खालीलप्रमाणे आहेत:
1. मूळ अवयव पाडून संख्यांचा लसावि (LCM) काढणे (प्राइम फॅक्टरायझेशन पद्धत)
दिलेल्या प्रत्येक संख्याला मूळ अवयवांचे गुणाकार म्हणून व्यक्त करा. LCM हे सर्व अवयवांच्या सर्वोच्च घातांक/घात कांचा गुणाकार असतो.
उदा. 60 व 48 यांचा लसावि काढा. प्रत्येक संख्येचे मूळ अवयव पाहू.
60 = 2 × 2 × 3 × 5, 48 = 2 × 2 × 2 × 2 × 3
वरील गुणाकारांत येणारी प्रत्येक मूळ संख्या पाहू.
2 ही संख्या जास्तीत जास्त 4 वेळा आली आहे. (48 च्या अवयवामध्ये)
3 ही संख्या जास्तीत जास्त 1 वेळा आली आहे. (60 च्या अवयवामध्ये)
5 ही संख्या जास्तीत जास्त 1 वेळा आली आहे. (60 च्या अवयवामध्ये)
∴ लसावि = 2 × 2 × 2 × 2 × 3 × 5 = 10 × 24 = 240
2. विभाज्यतेच्या कसोट्या वापरून
- विभाज्यतेच्या कसोट्या वापरून सर्व संख्यांना भाग जाणाऱ्या संख्या शोधा व तिने दिलेल्या संख्यांना भागा. भागाकाराने मिळालेल्या संख्यांसाठी हीच क्रिया शक्य तेवढ्या वेळा करा.
- आता मिळालेल्या संख्यांपैकी कमीत कमी दोन संख्यांंची विभाजक असलेली संख्या शोधून तिने ज्यांना भाग जातो त्या संख्यांना भागा. ज्या संख्येला भाग जात नाही, ती तशीच ठेवा. हीच क्रिया शक्य तेवढ्या वेळा करा.
- 1 शिवाय इतर कोणताही साधारण अवयव नसल्यास भागाकार थांबवा.
- डाव्या स्तंभातील संख्यांचा गुणाकार करा. त्याला सर्वांत खालच्या आडव्या ओळीतील संख्यांनी गुणा.
उदा. 16, 28 व 40 यांचा लसावि काढा.
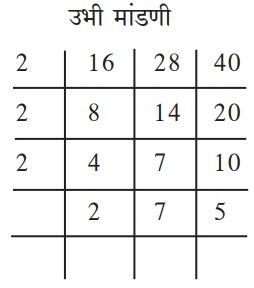
∴ लसावि = 2 × 2 × 2 × 2 × 5 × 7 = 560
काही महत्वाचे सोडवलेले प्रश्न
Q1. 204, 1190, आणि 1445 चा मसावि किती आहे?
(a) 17
(b) 18
(c) 19
(d) 21
Q2. दोन संख्यांचा मसावि आणि लसावि अनुक्रमे 12 आणि 336 आहे. जर एक संख्या 84 असेल तर दुसरी संख्या शोधा?
(a) 36
(b) 48
(c) 72
(d) 96
Q3. 500 पेक्षा कमी संख्या, 4, 5, 6, 7 ने भागल्यावर प्रत्येक बाबतीत 1 बाकी उरते. संख्या आहे
(a) 211
(b) 420
(c) 421
(d) 441
Q4. जर तीन संख्या 2a, 5a आणि 7a असतील तर त्यांचा लसावि किती असेल?
(a) 70a
(b) 65a
(c) 75a
(d) 70a
Q5. सहा घंटा एकत्रितपणे टोल सुरू करतात आणि अनुक्रमे 2, 4, 6, 8, 10 आणि 12 सेकंदांच्या अंतराने टोल देतात. 30 मिनिटांत, ते एकत्र किती वेळा टोल देतील?
(a) 4
(b) 15
(c) 10
(d) 16
Q6. 15, 25, 40 आणि 75 ने भाग जाणार्या चार अंकांची सर्वात मोठी संख्या किती आहे.
(a) 9000
(b) 9400
(c) 9800
(d) 9600
Q7. 148 आणि 185 चा लसावि काढा
(a) 680
(b) 740
(c) 2960
(d) 3700
Q8. 0.54, 1.8 आणि 7.2 चा मसावि काढा
(a) 1.8
(b) 0.18
(c) 0.018
(d) 18

स्पष्टीकरण
S1. Ans.(a)
Sol. 204, 1190, 1445 चा मसावि.
204 = 2 × 2 × 3 × 17
1190 = 2 × 5 × 7 × 17
1445 = 5 × 17 × 17
मसावि = 17
S2. Ans.(b)
Sol. मसावि × लसावि = पहिले संख्या × दुसरी संख्या
12 × 336 = 84 × x
x = 48
S3. Ans.(c)
Sol. 4, 5, 6, 7 चा लसावि = 420
420 + बाकी 1 = 421
421 हा 500 पेक्षा कमी आहे आणि 4, 5, 6, 7 ने भाग जातो.
S4. Ans.(a)
Sol. 2a, 5a, 7a चा लसावि
लसावि = 70a
S5. Ans.(d)
Sol. 2, 4, 6, 8, 10 आणि 12 चा लसावि
लसावि = 120 सेकंद
30 मिनिटांत, ते एकत्र किती वेळा 16 वेळा टोल देतील.
S6. Ans.(d)
Sol. 15, 25, 40 आणि 75 चा लसावि
लसावि = 600
चार अंकी सर्वात मोठी संख्या = 9999
15, 25, 40 आणि 75 ने भाग जाणारी सर्वात मोठी संख्या.
= 9999 ÷ 600
= 9999 – 399
= 9600
S7. Ans.(b)
Sol. 148 आणि 185 चा लसावि
148 = 2 × 2 × 37
185 = 5 × 37
लसावि = 2 × 2 × 37 × 5 = 740
S8. Ans.(b)
Sol. 0.54, 1.8 आणि 7.2 चा मसावि
= 0.54, 1.80, 7.20
= 0.18
महाराष्ट्रातील सर्व स्पर्धा परीक्षांसाठी ऑनलाईन क्लास, व्हिडिओ कोर्स, टेस्ट सिरीज, पुस्तके आणि इतर अभ्यास साहित्य खाली दिलेल्या लिंक वर क्लिक करून मिळावा.
| Latest Maharashtra Govt. Jobs | Majhi Naukri 2023 |
| Home Page | Adda 247 Marathi |
| Current Affairs in Marathi | Chalu Ghadamodi |
YouTube channel- Adda247 Marathi
Adda247 मराठी App | Add247Marathi Telegram group




