Correct option is C
Given:
Identity Used:
Solution:
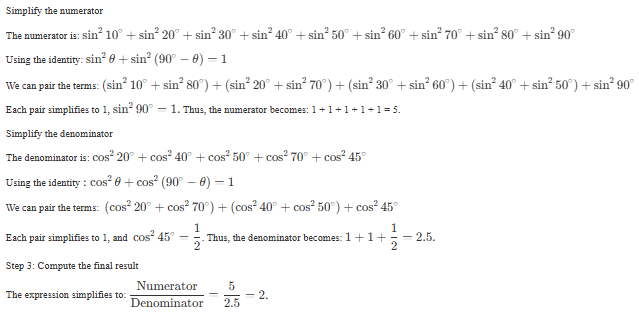
The value of is ?
Given:
Identity Used:
Solution:
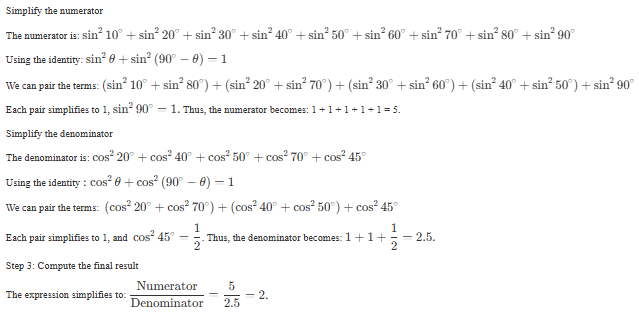
 English
English 100 Questions
100 Questions 90 Mins
90 Mins English
English English
English 100 Questions
100 Questions 90 Mins
90 Mins English
English English
English 40 Questions
40 Questions 25 Mins
25 Mins English
EnglishSimplify: cosecθ(1 – cosθ)(cosecθ + cotθ)
If cot A + cos A = p, cot A - cos A = q, then what is the value of p2- q2?
What is the value of sin 20° cos 10° + cos 20° sin 10°?
If sin x = and x ∈ (0, ), then find
Find the value of
If sin θ + cos θ = √3, then the value of tan θ + cot θ is:
If , then the value of the expression is:
If then the value of tan5θ is:
The value of the expression is:
The value of

Suggested Test Series






Suggested Test Series




