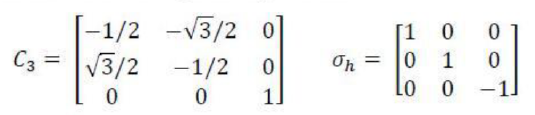Correct option is B
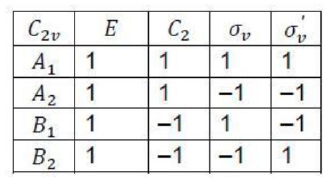
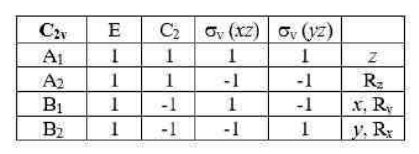
Reducible and Irreducible representation
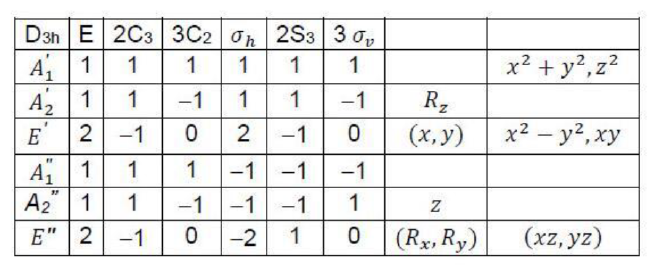
The C31representation of the point group C3v based on the bond vectors of NH3 molecule is
Let this matrix be subjected to a similarity transformation X-1AX where the matrix X is given by
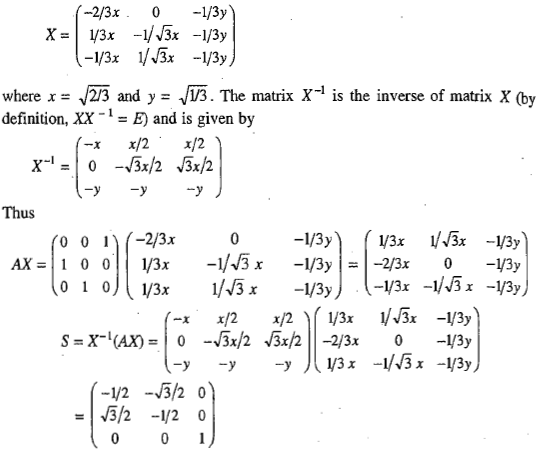
We find that the matrix A (which involves zeros along the diagonal and at the other places distributed unsymmetrically about the diagonal) is transformed into the matrix S (which involves zeros distributed symmetrically about the diagonal). Moreover, the nonzero elements in the matrix S are distributed along the diagonal into two blocks of the order 2×2 and 1× 1, respectively. If now the above similarity transformation involving the same matrices X and X-1 is extended to the corresponding matrices of the remaining symmetry operations of the point group C3v, we get
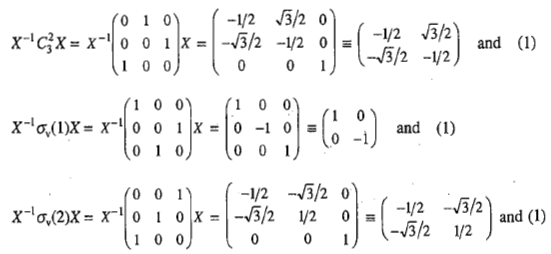
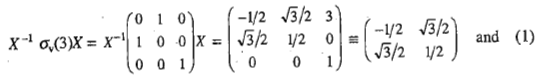
We find that each of the original matrix representation is changed into a matrix involving nonzero elements along the diagonal and each one is factored into two identically situated 2×2 and 1×1 blocks, respectively. We also find that the resultant matrices are identical to the matrix representations based on the translational vectors Tx and Ty (taken together) and Tz respectively. Thus, the above similarity transformation is equivalent to changing the basis of representation from bond vectors to translational vectors. Since the matrix A can be converted into two matrices of the lower orders by a suitable similarity transformation, the representation depicted by the matrix A is said to be reducible representation. If the resultant matrices cannot be reduced further by a similarity transformation, the corresponding representation is said to represent irreducible representation. The irreducible representations play fundamental role in the application of symmetry to molecular problems.
Once we know reducible representation of a group, we can find out the irreducible representations contained in it by using the expression
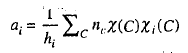

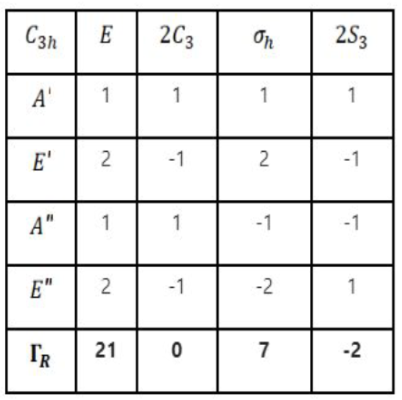
Order (hi) of C3h group is 6.
a(A')= (1/6)[1×1×21+2×1×0+1×1×7+2×1×(-2)]=4
a(A")= (1/6)[1×1×21+2×1×0+1×(-1)×7+2×(-1)×(-2)]=3