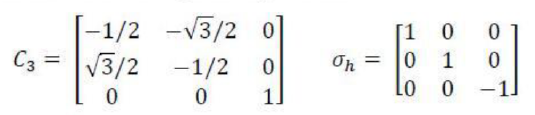Correct option is A
The systematic discussion of symmetry is called group theory. An action that leaves an object looking the same after it has been carried out is called a symmetry operation. Typical symmetry operations include rotations, reflections, and inversions. There is a corresponding symmetry element for each symmetry operation, which is the point, line, or plane with respect to which the symmetry operation is performed.
The classification of objects according to symmetry elements corresponding to operations that leave at least one common point unchanged gives rise to the point groups.
The identity, E, consists of doing nothing; the corresponding symmetry element is the entire object.
An n-fold rotation (the operation) about an n-fold axis of symmetry, Cn(the corresponding element) is a rotation through 360°/n. If a molecule possesses several rotation axes, then the one (or more) with the greatest value of n is called the principal axis.
A reflection (the operation) in a mirror plane, σ (the element), may contain the principal axis of a molecule or be perpendicular to it. If the plane is parallel to the principal axis, it is called ‘vertical’ and denoted σv. A vertical mirror plane that bisects the angle between two C2 axes is called a ‘dihedral plane’ and is denoted σd. When the plane of symmetry is perpendicular to the principal axis it is called ‘horizontal’ and denoted σh.
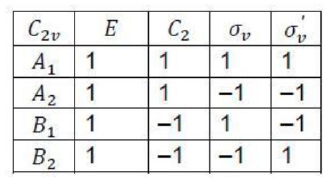
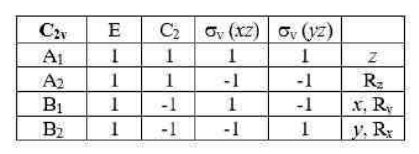
If in addition to the identity and a Cn axis a molecule has n vertical mirror planes σv, then it belongs to the group Cnv.
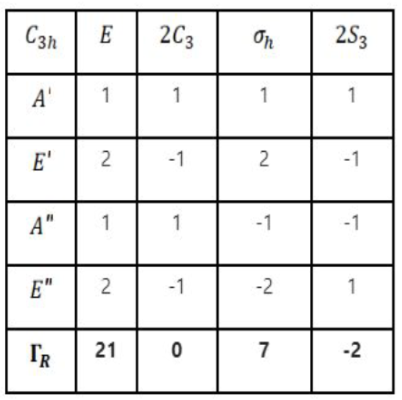
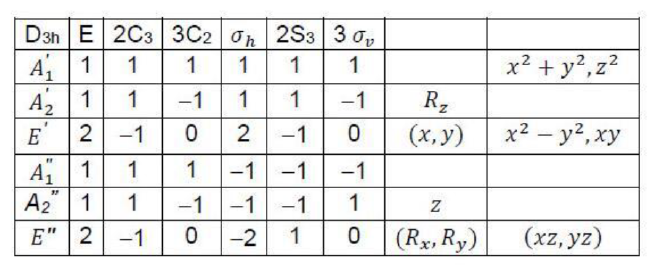
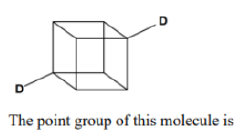
A molecule that has an n-fold principal axis and n twofold axes perpendicular to Cn belongs to the group Dn. A molecule belongs to Dnh if it also possesses a horizontal mirror plane. Sn represents the improper axis of symmetry which includes application of rotation followed by reflection or vice-versa.

In linear algebra, the trace of a square matrix A, denoted tr(A), is the sum of the elements on its main diagonal,

It is only defined for a square matrix (n × n).