Correct option is B
A crystal is built up from regularly repeating ‘structural motifs’, which may be atoms, molecules, or groups of atoms, molecules, or ions. A space lattice is the pattern formed by points representing the locations of these motifs. The unit cell is an imaginary parallelepiped (parallel-sided figure) that contains one unit of the translationally repeating pattern. A unit cell is commonly formed by joining neighbouring lattice points (A lattice in the sense of a 3-dimensional array of regularly spaced points coinciding with e.g. the atom or molecule positions in a crystal) by straight lines. Such unit cells are called primitive. A primitive unit cell (with lattice points only at the corners) is denoted P. A face-centred unit cell (F) has lattice points at its corners and also at the centres of its six faces.
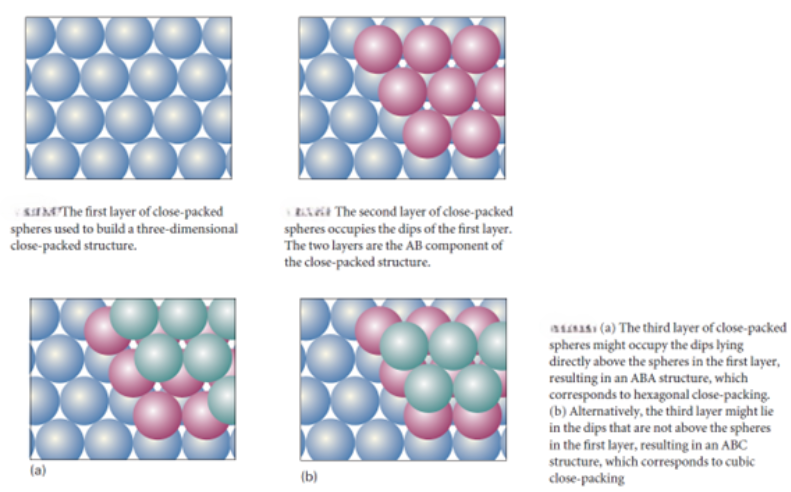
A close-packed layer of identical spheres, one with maximum utilization of space. A close-packed three-dimensional structure is obtained by stacking such close-packed layers on top of one another. In all polytypes, the spheres of second close-packed layer lie in the depressions of the first layer.
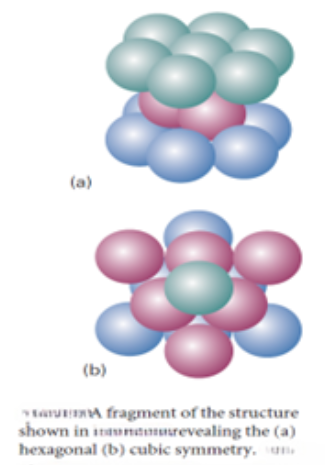
The third layer may be added in either of two ways. In one, the spheres are placed so that they reproduce the first layer, to give an ABA pattern of layers. Alternatively, the spheres may be placed over the gaps in the first layer, so giving an ABC pattern. Two polytypes are formed if the two stacking patterns are repeated in the vertical direction. If the ABA pattern is repeated, to give the sequence of layers ABABAB..., the spheres are hexagonally close-packed(hcp). Alternatively, if the ABC pattern is repeated, to give the sequence ABCABC..., the spheres are cubic close-packed (ccp). The ccp structure gives rise to a face-centred unit cell, so may also be denoted cubic F (or fcc, for face-centred cubic). Strictly speaking, ccp refers to a close-packed arrangement whereas fcc refers to the lattice type of the common representation of ccp. However, this distinction is rarely made.
In closest-packing two types of holes are observed: (i) tetrahedral hole, and (ii) octahedral hole. The tetrahedral hole is formed when a sphere fits into the depression formed by three other spheres closest-packed (forming an equilateral triangle) in two dimensions. In two closest-packed layers, there is such a hole above each atom in the first layer and below each atom in the second layer. In a multilayered closest-packed structure, there is a tetrahedral hole above and below each atom; hence there are twice as many tetrahedral holes as there are closest-packed atoms. The octahedral hole is formed when the three closest-packed spheres of one layer (forming an equilateral triangle) is put over three closest-packed spheres of the second layer, their positions being inverted with respect to each other.
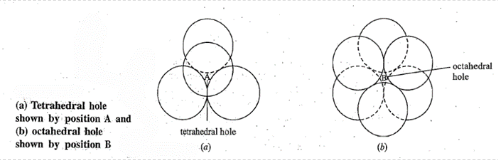
In a closest-packed structure, the number of octahedral holes is equal to the number of atoms present and they are located midway between the two closest-packed layers. The positions of these two holes relative to those of the two closest-packed layers are shown below:
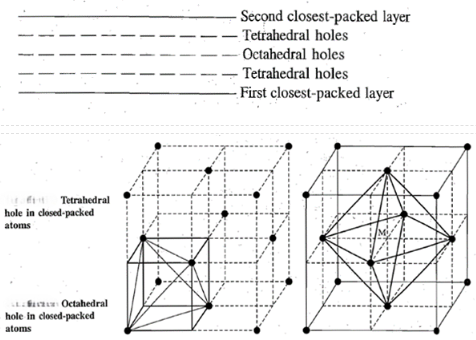
The atoms in one small cube actually touch one another. Since these atoms are at alternate corners of the cube they form a tetrahedron with a hole in the centre. The entire unit cell contains eight tetrahedral holes, one in each small cube. Since there are four atoms per cubic unit cell, there will be two tetrahedral holes per closest-packed atom.
The intersections of the lines at M are not occupied by an atom and this is surrounded by six atoms at the corners of an octahedron. This intersection becomes an octahedral hole when the atoms just touch one another: Besides the intersection M, there are twelve more intersections at the centres of the edges. Since each edge is common to four-unit cells, there are only three intersections (holes) from edges that belong completely to one unit cell. Thus, in all we have four octahedral holes in one unit cell and hence one octahedral hole per closest-packed atom.
The face-centered cubic lattice (cF) has lattice points on the faces of the cube, that each gives exactly one half contribution, in addition to the corner lattice points, giving a total of four lattice points per unit cell (1/8 × 8 from the corners plus 1/2 × 6 from the faces).
A(4/2)+(8/2)B4=A6B4=A3B2.