Table of Contents
पायथागोरस प्रमेय
पायथागोरस प्रमेय मुळात काटकोन त्रिकोणाच्या बाजू एकमेकांशी कशा संबंधित आहेत हे स्पष्ट करते. पायथागोरसचे प्रमेय असे सांगते की त्रिकोणाचा कर्ण वर्ग हा इतर दोन बाजूंच्या वर्गांच्या बेरजेइतका असतो. पायथागोरस प्रमेय आपल्याला कर्णाची लांबी, लंब आणि काटकोन त्रिकोणाच्या पायासह त्रिकोणाचा कोन शोधण्यात मदत करते. येथे आपण पायथागोरस प्रमेय, त्याचे सूत्र, त्याची समीकरणे आणि सोडवलेल्या उदाहरणांसह व्युत्पत्तीबद्दल अधिक जाणून घेऊया, चला शिकूया.
पायथागोरस प्रमेय सूत्र
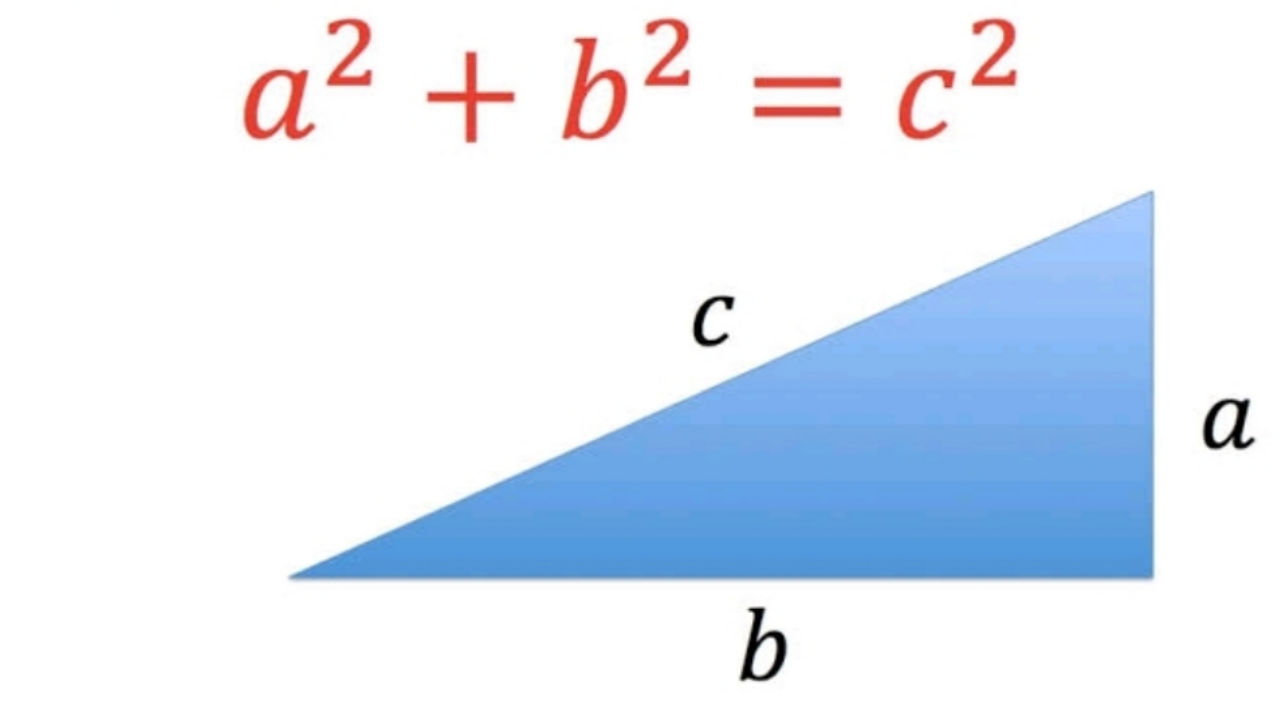
पायथागोरस प्रमेय सूत्र: पायथागोरस प्रमेयाचे सूत्र जाणून घेण्यापूर्वी, काटकोन त्रिकोणाचे द्रुत पुनरावलोकन करूया कारण पायथागोरस प्रमेय मुख्यत्वे दाखवते की काटकोन त्रिकोणाच्या बाजू एकमेकांशी कशा संबंधित आहेत. काटकोन त्रिकोण. काटकोनात नेहमी 90° कोन असतो. हायपोटेनस, बेस आणि लंब ही तीन बाजूंची नावे आहेत जी काटकोन बनवतात. सर्वात लांब बाजू नेहमीच कर्ण असते. कर्ण 90° कोन विरुद्ध असलेली बाजू आहे इतर दोन आतील कोन 90 अंशांपर्यंत जोडतात.
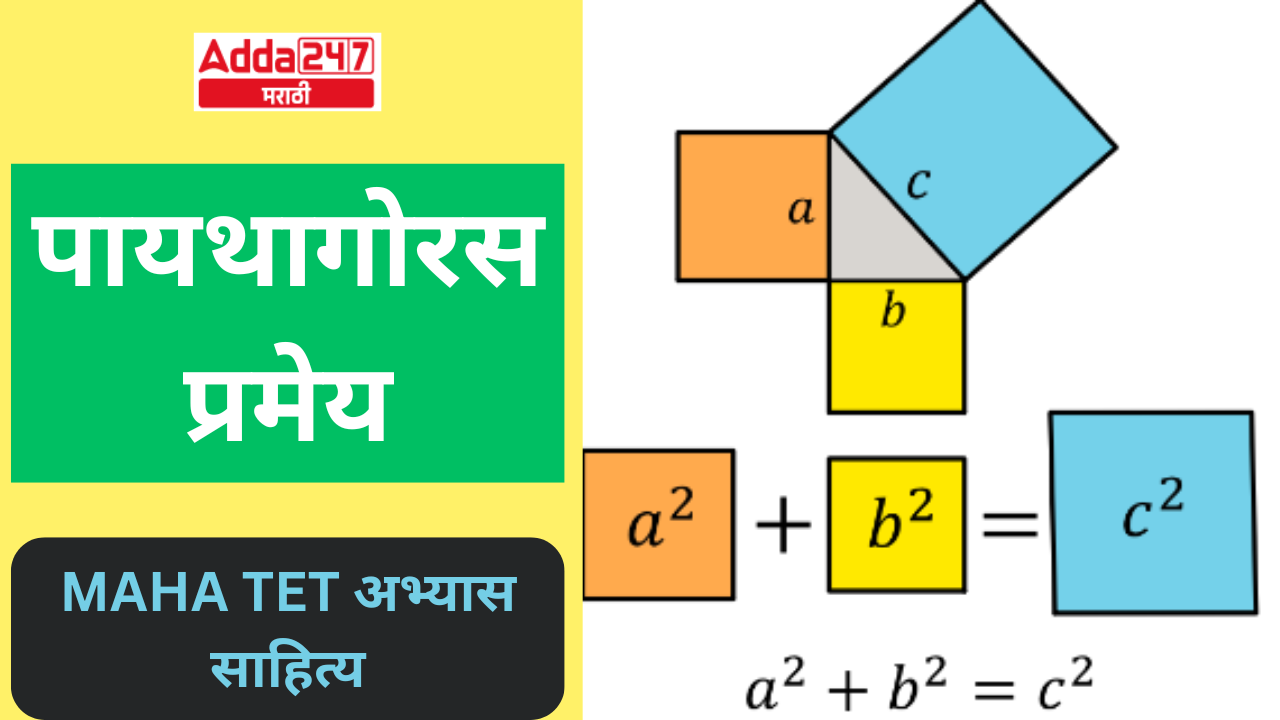
पायथागोरसच्या प्रमेयानुसार, काटकोन त्रिकोणाच्या कर्णाचा वर्ग इतर दोन बाजूंच्या वर्गांच्या बेरजेइतका असतो. हे प्रमेय पायथागोरियन समीकरण म्हणून व्यक्त केले जाऊ शकते, जे काटकोन त्रिकोण a, b आणि कर्ण c च्या तीन बाजूंच्या लांबीमधील संबंध आहे.
लंब² + पाया² = कर्ण²
a² + b² = c²
चला ABC त्रिकोण गृहीत धरू, जिथे BC ² = AB ² + AC ² उपस्थित आहे. या समीकरणात पाया AB द्वारे, उंची AC द्वारे आणि कर्ण BC द्वारे दर्शविला जातो.
पायथागोरसचे प्रमेय प्रथम सामोसचे ग्रीक गणितज्ञ पायथागोरस यांनी मांडले. ते क्लासिक ग्रीक परंपरेचे तत्त्वज्ञ होते. 569 बी सी मध्ये सामोसच्या ग्रीक बेटावर जन्मलेल्या, समोसच्या पायथागोरसने इजिप्तमध्ये मोठ्या प्रमाणावर प्रवास केला जेथे त्याने गणित आणि इतर विषयांचा अभ्यास केला. त्यांनी कठोर शिस्तीचा अभ्यास करणाऱ्या गणितज्ञांचा समुदाय स्थापन केला. शेवटी, ग्रीक गणितज्ञांनी पायथागोरसचे प्रमेय सिद्ध केले; परिणामी, त्याच्या सन्मानार्थ “पायथागोरस प्रमेय” म्हणून ओळखले जाते.
पायथागोरस प्रमेय पुरावा
पायथागोरस प्रमेय प्रदर्शित करण्याचे अनेक मार्ग आहेत. बीजगणित पद्धत आणि समान त्रिकोण वापरण्याची पद्धत पायथागोरसचे प्रमेय सिद्ध करण्याच्या दोन सर्वात लोकप्रिय पद्धती आहेत. या प्रमेयाचा पुरावा समजून घेण्यासाठी, या प्रत्येक पद्धतीचा स्वतंत्रपणे सखोल विचार करूया.
बीजगणितीय पद्धत वापरून पायथागोरस प्रमेय पुरावा
पायथागोरियन प्रमेय बीजगणिताचा वापर करून खालील आकृतीचा वापर करून सिद्ध केले. चार काटकोन त्रिकोणांच्या कर्णाच्या समान बाजू असलेला एक मोठा चौकोन आणि आतील चौकोन तयार केला आहे.
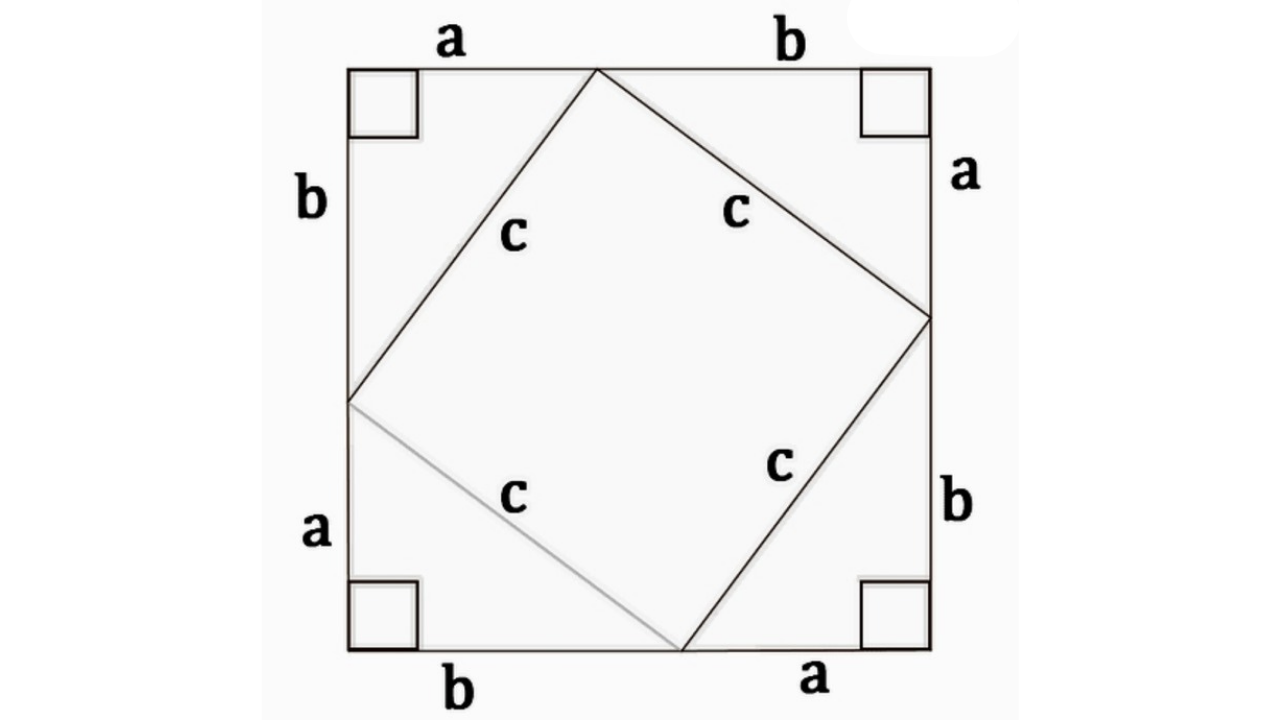
त्रिकोणाचे पाय a आणि b लांबीचे आहेत आणि त्यांचे कर्ण c लांबीचे आहेत. मोठ्या चौरसाच्या बाजू ज्या मोजमाप तयार करतात (a + b). त्यामुळे त्याचे क्षेत्रफळ (a+b)² च्या समतुल्य आहे
आतील चौरस बाजूंची लांबी c आहे हे दिले तर त्याचे क्षेत्रफळ आहे c².आम्ही हे देखील पाहू शकतो की मोठ्या चौरसाचे क्षेत्रफळ चार त्रिकोणांच्या क्षेत्रफळाच्या आणि आतील चौकोनाच्या बेरजेइतके आहे. परिणामी, आमच्याकडे आहे:
(a+b)² =4(½×a× b) + c²
a² + b² +2ab = 2ab+ c²
a² + b² =c² (सिद्ध)
समान त्रिकोण वापरून पायथागोरस प्रमेय पुरावा
- जेव्हा दोन त्रिकोणांच्या संगत बाजू आणि कोन समान आकार आणि गुणोत्तर असतात, तेव्हा आपण असे म्हणू शकतो की दोन्ही त्रिकोण समान आहेत.
पायथागोरसचे प्रमेय आपण समान त्रिकोण वापरून कसे सिद्ध करू शकतो ते पाहू.
- काटकोन त्रिकोणामध्ये, कर्ण काटकोन शिरोबिंदूपासून घेतलेल्या उंचीने दोन तुकड्यांमध्ये विभागला जातो.
- परिणामी दोन लहान काटकोन त्रिकोण एकमेकांसारखे आहेत.
- तीन त्रिकोणांच्या तीन बाजू एकत्रितपणे मोजा.
- तीन त्रिकोणांच्या संबंधित बाजू एकमेकांच्या प्रमाणात आहेत कारण ते तुलनात्मक त्रिकोण आहेत.
- संबंधित बाजूंच्या गुणोत्तरांचा विचार करा.
- समीकरणांमधून, मूळ त्रिकोणाच्या बाजूंचे वर्ग मिळवा.
- पायथागोरियन प्रमेय सिद्ध करण्यासाठी बाजूंच्या चौकोनांचा वापर करा.
- नंतर, कर्णाच्या वर्गाप्रमाणे बेरीज आहे की नाही हे निश्चित करा.
पायथागोरस प्रमेय हायपोटेनस फॉर्म्युलाची व्युत्पत्ती
कल्पना करा की त्रिकोण ABC, जो B वर काटकोन आहे. AC वर D ला लंब BD तयार करा. पायथागोरसचे प्रमेय सिद्ध करण्यासाठी संबंधित त्रिकोण वापरा.
△ABD आणि △ACB त्रिकोणामध्ये,
∠A = ∠A (दोन्ही त्रिकोणांचे सामाईक कोन)
∠ABC = ∠ADB (दोन्ही कोन काटकोन आहेत)
म्हणून, △ABD ∼△ACB (AA समानता निकषानुसार)
आपण असेच दाखवू शकतो की△ BCD =△ ACB.
परिणामी, △ABD ∼ △ACB,
AD/AB = AB/AC. आपण असे सांगू शकतो की AD × AC = AB².
त्याचप्रमाणे, आपण सिद्ध करू शकतो की △BCD ∼ △ACB.
म्हणून, CD/BC = BC/AC याव्यतिरिक्त, आपण म्हणू शकतो, CD × AC = BC².
ही दोन समीकरणे एकत्र करून आपण मिळवतो-
AB² + BC² = (AD × AC) + (CD × AC)
AB²+ BC² =AC(AD +DC)
AB² + BC² =AC² [ सिद्ध ]
पायथागोरस प्रमेय मॉडेल
पायथागोरसच्या प्रमेयानुसार काटकोन त्रिकोणामध्ये कर्णाच्या बाजूचा वर्ग इतर दोन बाजूंच्या वर्गांच्या बेरजेइतका असतो. या त्रिकोणाच्या तीन बाजूंना लंब, पाया आणि हायपोटेनस असे म्हणतात.
हे प्रमेय पायथागोरियन समीकरण म्हणून व्यक्त केले जाऊ शकते, जे काटकोन त्रिकोण a, b आणि कर्ण c च्या तीन बाजूंच्या लांबीमधील संबंध आहे.
लंब² + पाया² = कर्ण²
a² + b² = c²
पायथागोरस प्रमेय अनुप्रयोग
पायथागोरस प्रमेय कसे लागू केले जाते याची अनेक उदाहरणे समाविष्ट आहेत
- पायथागोरियन प्रमेय वारंवार काटकोन त्रिकोणाच्या बाजूंची लांबी निर्धारित करण्यासाठी वापरला जातो.
- पायथागोरस प्रमेय वापरून आपण पाया, लंब आणि कर्ण हे सूत्र मिळवू शकतो.
- आयत, चौरस इ.ची कर्ण लांबी निश्चित करण्यासाठी, प्रमेय वापरा.
- पायथागोरस प्रमेयच्या संभाषणाचा वापर करून त्रिकोणाची शुद्धता निश्चित केली जाते.
- त्रिकोणमितीमध्ये, पायथागोरस प्रमेय sin, cos, tan, cosec, sec आणि cot यांसारखे त्रिकोणमितीय गुणोत्तर निर्धारित करण्यासाठी वापरले जाते.
- अभियांत्रिकी आणि इमारत या विषयांमध्ये, आर्किटेक्ट पायथागोरस प्रमेय दृष्टिकोन लागू करतात.
- पर्वत सर्वेक्षणासाठी पायथागोरस प्रमेय लागू करणे
- नेव्हिगेशनमध्ये सर्वात लहान मार्ग शोधणे हा दुसरा अनुप्रयोग आहे.
- डोंगर किंवा टेकडीचा उतार किती उंच आहे याची गणना करण्यासाठी प्रमेय आवश्यक आहे.
पायथागोरस प्रमेय आधारित प्रश्न
Q.4 सेमी आणि 3 सेमी लांबीच्या दोन बाजू असलेला QA त्रिकोण. त्रिकोणाच्या कर्णाची लांबी किती आहे?
उपाय.पायथागोरस प्रमेयाच्या सूत्रानुसार, लंब² + पाया² = कर्ण²
दिलेल्या समस्येमध्ये, पाया = 4 सेमी, लंब = 3 सेमी.
पायथागोरसच्या प्रमेयानुसार,
कर्ण² = 4² + 3²
कर्ण² = 16+ 9 = 25
कर्ण =√25 = 5 सेमी
महाराष्ट्रातील सर्व स्पर्धा परीक्षांसाठी ऑनलाईन क्लास, व्हिडिओ कोर्स, टेस्ट सिरीज, पुस्तके आणि इतर अभ्यास साहित्य खाली दिलेल्या लिंक वर क्लिक करून मिळावा.
अड्डा 247 मराठीचे युट्युब चॅनल
अड्डा 247 मराठी टेलिग्राम ग्रुप
महाराष्ट्र महापॅक