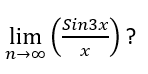Correct option is B
At x = π 4 , we have: cot x = tan − 1 x = 1 => cot 3 x = 1 tan x = 1 cos ( x + π 4 ) = cos ( π 2 ) = 0 So, the limit becomes 0 0 , which is indeterminate. Apply L’H o ˆ pital’s Rule: Differentiate numerator: d d x ( cot 3 x − tan x ) = d d x ( cot 3 x ) − d d x ( tan x ) = 3 cot 2 x ⋅ ( − csc 2 x ) − sec 2 x = − 3 cot 2 x csc 2 x − sec 2 x Differentiate denominator: d d x [ cos ( x + π 4 ) ] = − sin ( x + π 4 ) Now evaluate at x = π 4 : cot x = 1 => cot 2 x = 1 csc x = 1 sin x = 2 => csc 2 x = 2 sec x = 1 cos x = 2 => sec 2 x = 2 sin ( π 2 ) = 1 So the expression becomes: lim x → π 4 − 3 ( 1 ) ( 2 ) − 2 − 1 = − 6 − 2 − 1 = − 8 − 1 = 8 \begin{aligned}&\text{At } x = \frac{\pi}{4}, \text{ we have:} \\&\quad \cot x = \tan^{-1} x = 1 \Rightarrow \cot^3 x = 1 \\&\quad \tan x = 1 \\&\quad \cos\left(x + \frac{\pi}{4} \right) = \cos\left(\frac{\pi}{2} \right) = 0 \\[10pt]&\text{So, the limit becomes } \frac{0}{0}, \text{ which is indeterminate. Apply L'Hôpital's Rule:} \\&\text{Differentiate numerator:} \\&\frac{d}{dx}(\cot^3 x - \tan x) = \frac{d}{dx}(\cot^3 x) - \frac{d}{dx}(\tan x) \\&= 3 \cot^2 x \cdot (-\csc^2 x) - \sec^2 x = -3 \cot^2 x \csc^2 x - \sec^2 x \\[10pt]&\text{Differentiate denominator:} \\&\frac{d}{dx} \left[\cos\left(x + \frac{\pi}{4} \right)\right] = -\sin\left(x + \frac{\pi}{4} \right) \\[10pt]&\text{Now evaluate at } x = \frac{\pi}{4}: \\&\quad \cot x = 1 \Rightarrow \cot^2 x = 1 \\&\quad \csc x = \frac{1}{\sin x} = \sqrt{2} \Rightarrow \csc^2 x = 2 \\&\quad \sec x = \frac{1}{\cos x} = \sqrt{2} \Rightarrow \sec^2 x = 2 \\&\quad \sin\left(\frac{\pi}{2} \right) = 1 \\[10pt]&\text{So the expression becomes:} \\&\lim_{x \to \frac{\pi}{4}} \frac{-3(1)(2) - 2}{-1} = \frac{-6 - 2}{-1} = \frac{-8}{-1} = {8}\end{aligned} At x = 4 π , we have: cot x = tan − 1 x = 1 => cot 3 x = 1 tan x = 1 cos ( x + 4 π ) = cos ( 2 π ) = 0 So, the limit becomes 0 0 , which is indeterminate. Apply L’H o ˆ pital’s Rule: Differentiate numerator: d x d ( cot 3 x − tan x ) = d x d ( cot 3 x ) − d x d ( tan x ) = 3 cot 2 x ⋅ ( − csc 2 x ) − sec 2 x = − 3 cot 2 x csc 2 x − sec 2 x Differentiate denominator: d x d [ cos ( x + 4 π ) ] = − sin ( x + 4 π ) Now evaluate at x = 4 π : cot x = 1 => cot 2 x = 1 csc x = sin x 1 = 2 => csc 2 x = 2 sec x = cos x 1 = 2 => sec 2 x = 2 sin ( 2 π ) = 1 So the expression becomes: x → 4 π lim − 1 − 3 ( 1 ) ( 2 ) − 2 = − 1 − 6 − 2 = − 1 − 8 = 8





 is continuous at x = π, then the value of k is
is continuous at x = π, then the value of k is