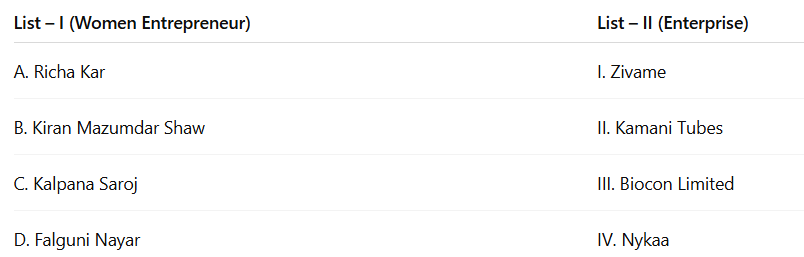
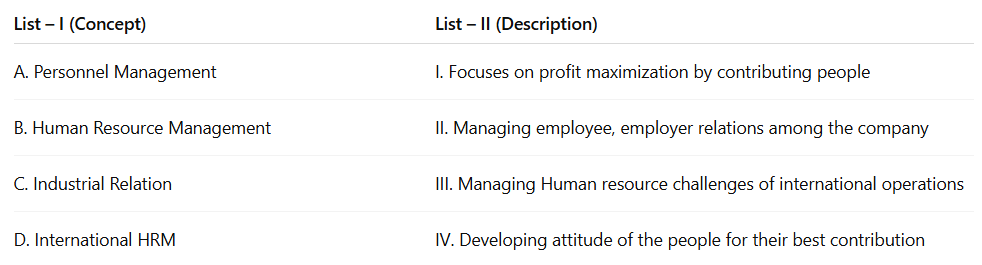
Correct option is C
To find the standard deviation of the first 'n' natural numbers, we follow this process:
Let the first ‘n’ natural numbers be:
1, 2, 3, ..., n.

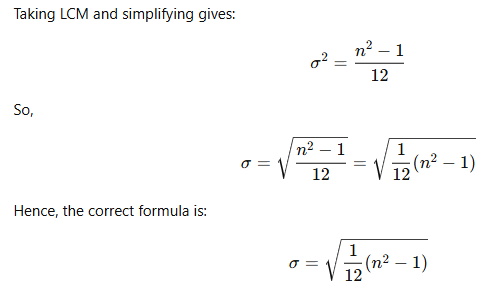
Information Booster:
Standard deviation measures the dispersion of data points from the mean.
For first ‘n’ natural numbers, values are uniformly distributed, allowing formula derivation.
Variance formula uses the difference of square of mean and mean of squares.
This specific derivation only applies to the first n natural numbers, not general sequences.
The standard deviation result shows a square root relationship with quadratic terms, showing how spread increases with larger n.
Additional Knowledge:
- Option a) gives a higher value than actual standard deviation due to larger denominator factor being 6.
- Option b) alters both the numerator and denominator from the actual variance formula, resulting in overestimation.
- The structure of Option d) is similar but the numerator inside the root uses n2 + 1 instead of n2 - 1 , giving a slightly increased value from the accurate standard deviation.





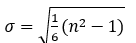
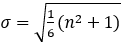
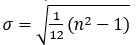
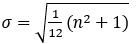
 English
English 50 Questions
50 Questions 60 Mins
60 Mins