The correct statement(s) for oxygen from the following

A. The ground state for the O atom is ³P₁.
B. Both the atom and the diatomic molecule are paramagnetic with two unpaired electrons.
C. The most readily accessible singlet excited state for dioxygen has an empty $\pi$ orbital.

is/are

Choose the correct answer from the options given below:

Correct option is B

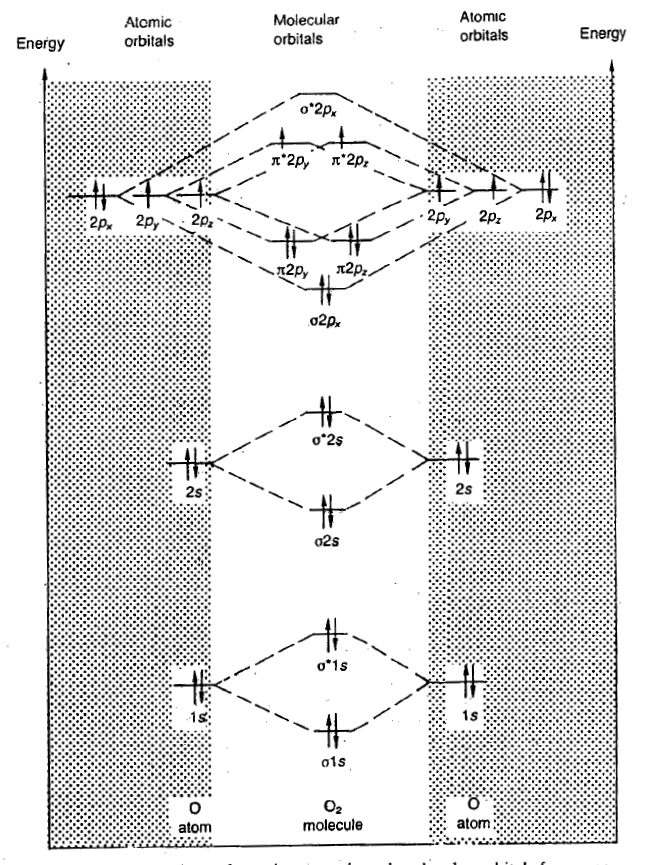
Each oxygen atom has 2+6=8 electrons. Thus the O₂ molecule contains a total of 16 electrons. These are arranged in MOs:

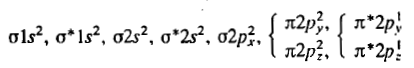
​The antibonding π^*2p_y  and π^*2p_z orbitals are singly occupied in accordance with Hund's rule. Unpaired electrons give rise to paramagnetism. Since there are two unpaired electrons with parallel spins, this explains why oxygen is paramagnetic.

The bond order may be calculated as half the difference between the number of bonding and antibonding electrons:In the case of O₂ the bond order is calculated as (10 - 6)/2 = 2, which corresponds to a double bond.

Term symbol for O atom ([He] 2s²2p⁴): Two electrons will be present in one of the p orbitals and will cancel each other.