Suppose a B⁺ tree is used for indexing a database file. Consider the following information:
Size of the search key field = 10 bytes
Block size = 1024 bytes
Size of the record pointer = 9 bytes
Size of the block pointer = 8 bytes
Let K be the order of the internal node and L be the order of the leaf node of B⁺ tree, then (K, L) = ______.

Correct option is A

This problem requires calculating the order of internal nodes (K) and leaf nodes (L) of a B-Tree based on the provided parameters.
Given Information:
1. Search Key Field Size = 10 bytes
2. Block Size = 1024 bytes
3. Record Pointer Size = 9 bytes
4. Block Pointer Size = 8 bytes
Calculation of K (Order of Internal Node):
In a B-Tree, the order of the internal node K is calculated based on the following formula:

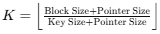
Here:
· Key Size = 10 bytes
· Pointer Size = 8 bytes
· Block Size = 1024 bytes
Substituting values:

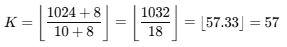
Thus, K = 57.
Calculation of L (Order of Leaf Node):
In the leaf node, we store:
1. Search Key Field (10 bytes per key)
2. Record Pointer (9 bytes per key)
3. One Block Pointer (8 bytes for the next leaf pointer).
The formula for L is:

Thus, L = 53.
The values of K and L are: (57, 53)
Information Booster:
1. Internal Node in B-Tree:
· Stores keys and pointers to child nodes.
· The number of pointers is one more than the number of keys.
2. Leaf Node in B-Tree:
· Contains keys and record pointers (points to the actual data).
· Typically includes a pointer to the next leaf node for sequential access.
3. B-Tree Properties:
· All nodes (except the root) must be at least half full.
· Root can have a minimum of 1 key.
· Ensures balanced height and efficient search.
Additional Knowledge:
· Pointer Sizes: Block pointers are typically smaller than record pointers because they reference other blocks in the index structure.
· Order of a B-Tree: Higher order K or L reduces the tree's height, improving search efficiency.
· Applications of B-Trees: Widely used in database indexing and file systems (e.g., NTFS, HFS+).