​Number of circles through a pair of given points​

Correct option is C

Given:
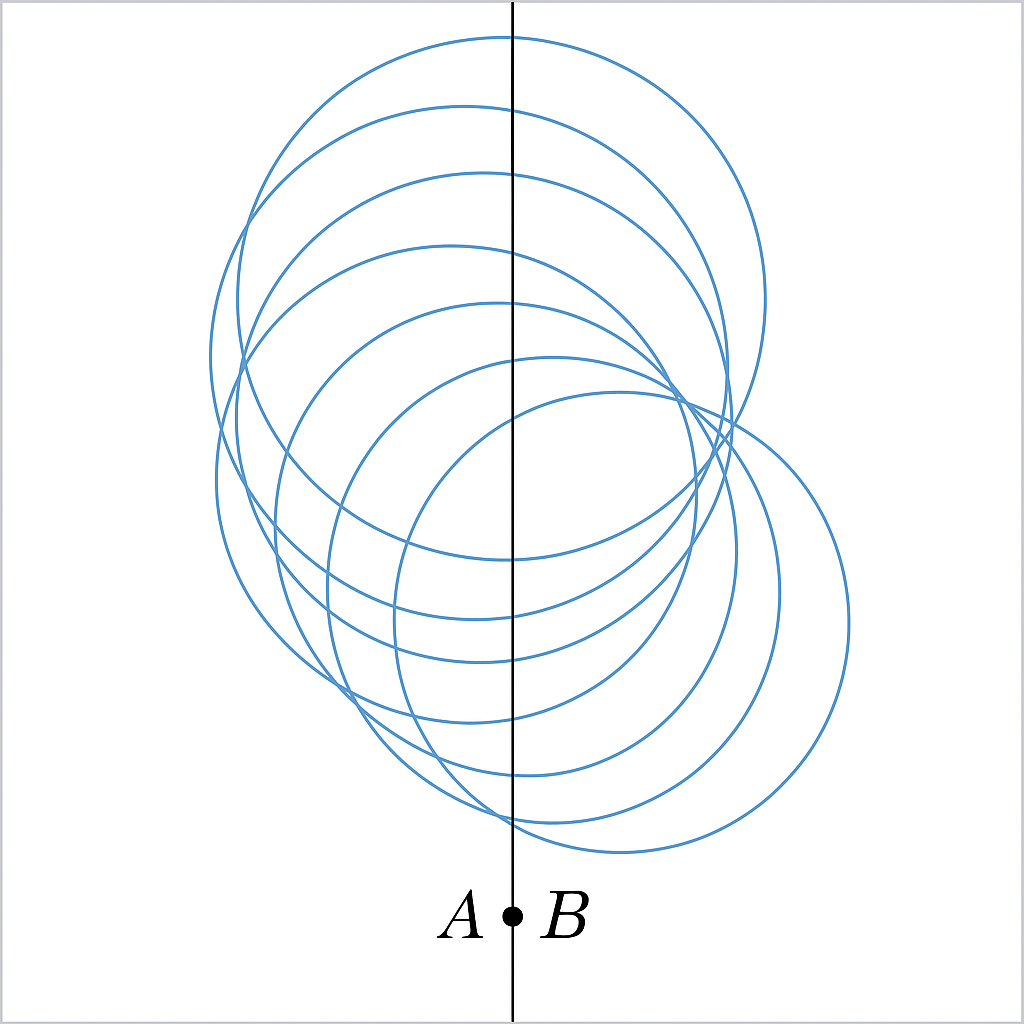
A pair of distinct points in a plane.
Concept used:
A circle is uniquely determined if its center and radius are fixed.
Through two given points, we can draw infinitely many circles because we can choose infinite possible centers on the perpendicular bisector of the segment joining these two points.
Solution:
The two points lie on the circumference.
The center of the circle must lie on the perpendicular bisector of the line joining these two points.
There are infinitely many such centers possible.
Correct answer is (C) – infinite