Let AB and CD be two parallel lines and PQ be a transversal such that PQ intersects AB at the point R and CD at the point S, respectively. If ∠BRP = (2x + 13)° and ∠DSP = (3x − 22)°, then find ∠CSP.

Correct option is C

Given:
Let AB and CD be two parallel lines and PQ be a transversal such that PQ intersects AB at the point R and CD at the point S, respectively. If ∠BRP = (2x + 13)° and ∠DSP = (3x − 22)°, then find ∠CSP.
Solution:

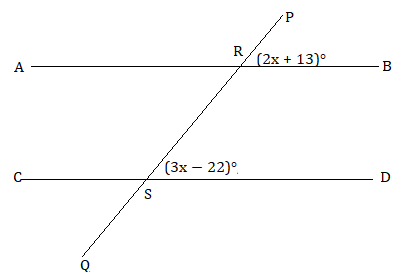
Since AB ∥ CD and PQ is a transversal, ∠BRP and ∠DSP are alternate interior angles.
According to the alternate interior angle theorem, alternate interior angles are congruent when two parallel lines are cut by a transversal.
Therefore, we can set the angles equal to each other:
∠BRP = ∠DSP
(2x + 13)° = (3x − 22)°
13 = x - 22
13 + 22 = x
x = 35
∠DSP = 3(35) - 22 = 105 - 22 = 83°
∠CSP = 180°- 83° = 97°
​