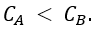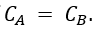Correct option is C

​Given:
The integral is:

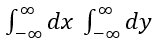
exp[-(x² + y² + 2axy)],
where $a$ is a real parameter. We need to determine the range of values for $a$ such that the integral is finite.​

Solution:

1. Rewrite the quadratic expression inside the exponential:
   The term x² + y² + 2axy can be rewritten as:
   (x + ay)² + (1 - a²)y².

2. Condition for the integral to converge:
   The integral converges if the expression inside the exponential remains positive for all x and y. For this to happen, the coefficient of y², which is (1 - a²), must be strictly greater than zero.

3. Solve for "a":
   The condition (1 - a²) > 0 implies:
   -1 < a < 1.

4. Boundary behavior:
   At a = 1 or a = -1, the coefficient of y^2 becomes zero, and the quadratic term becomes degenerate, causing the integral to diverge.

Conclusion:
The range of values of "a" for which the integral is finite is (c) -1 < a < 1.