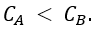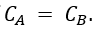Formula used : $$\binom{n}{r} = \frac{n!}{r!(n-r)!}$$​

Solution : 

Total number of ways to choose two people :The total ways to select two people from the group of 7:
​$$\binom{7}{2} = \frac{7 \times 6}{2} = 21$$

Total Sibling Pairs:

From the first group (4 people with one sibling):2 pairs

From the second group (3 people with two siblings):3 pairs
Total sibling pairs=2+3=5

The probability that two randomly selected people are not siblings is given by:

​$$P(\text{not siblings}) = \frac{\text{Number of non-sibling pairs}}{\text{Total pairs}} = \frac{16}{21}$$

 Thus the Correct Answer is option (B) $$\frac{16}{21}$$​​

​